Погрешность единицы веса
Обработку неравноточных измерений данных нельзя производить по формулам равноточных измерений, т.к. более точные измерения, очевидно, должны оказывать и большее влияние на окончательный результат. Различная точность измерений учитывается при совместной обработке их результатов путем введения вспомогательных величин, называемых весами. Чем надежнее результат измерения, тем меньше соответствующая ему средняя квадратическая погрешность и тем больше его вес. Вес – это величина, обратно пропорционалъная квадрату средней квадратической погрешности, характеризующей результат данного измерения: р = где k– произвольно выбранное число. Свойства весов: 1 Вес – понятие относительное, т.е. он не имеет размера. 2 Все веса можно увеличивать или уменьшать в одно и то же количество раз. 3 Веса можно учитывать только сравнивая их друг с другом. Понятие веса применимо и для любой функции F измеренных величин. Вес рFфункции Fпри известной её средней квадратической погрешности mFвычисляют по формуле рF = Средние квадратические погрешности неравноточных результатов не дают общей характеристики точности полученных результатов. В этом случае пользуются средней квадратической погрешностью единицы веса m, т.е. погрешностью результата с весом, равным единице р0 = 1 = Установим связь между средней квадратической погрешностью единицы веса m и средней квадратической погрешностью m результата измерения с весом р =
т.е. средняя квадратическая погрешность единицы веса m равна средней квадратической погрешности результата измерения, умноженной на квадратный корень из его веса. Если имеется ряд неравноточных измерений с весами р1, р2, …, рnи средними квадратическими погрешностями m1, m2, …, mn, то для каждого результата погрешности единицы веса будут:
...............
Среднее квадратическое значение из этого ряда будет m2 = m = Если заменить квадраты средних квадратических погрешностей m квадратами истинных Dили квадратами вероятнейших ошибок V, то формула (36) примет вид m =
|
(32)
(33)
(34)
. Отношение весов 
, откуда
, (35)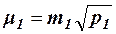
,
,
.
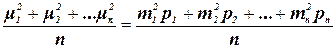, откуда
(36)
(37)
