Лекция 1. Основные сведения о матрицах
Лекция 1. Основные сведения о матрицах
На практике обширный числовой материал очень часто записывается в виде таблиц. Пусть некая фирма производит товары трех наименований А, В, С и поставляет их в четыре магазина. Тогда объемы поставки за какой-то определенный день, например 1 сентября 2010 г., менеджер отдела сбыта может записать в виде таблицы
Из таблицы видно, что в этот день фирма поставила магазину № 1 одно изделие А, два изделия В, а изделий С не поставляла. Магазину № 2 было поставлено два изделия А, три изделия В и одно изделие С и т.д. При каждодневной поставке менеджеру нет необходимости каждый раз писать «шапку» таблицы (он ее запоминает наизусть). Поэтому эту таблицу можно представить в следующем виде:
Такая таблица в математике называется матрицей.
Матрица — это прямоугольный массив чисел, записанный в форме строк и столбцов. Каждое число в матрице называется элементом матрицы.
Чаще всего матрица заключается в круглые скобки, но в литературе встречаются и другие обозначения. Например, вместо (…) пишут […] или ||…||. Размерностью матрицы называется совокупность двух чисел, состоящая из числа ее строк m и числа столбцов n. Обычно пишут Будем обозначать матрицы большими латинскими буквами А, В, С и т.д., а элементы матриц — соответствующими им малыми латинскими буквами с двумя индексами aij, bij, cij и т.д.: первый индекс i обозначает номер строки, в которой находится данный элемент, а второй индекс j — номер столбца. Индексы i, j определяют адрес элемента матрицы. Тогда в общем виде матрица размерностью
Иногда используют сокращенную запись матрицы А в виде Если m = n, то матрицу называют квадратной матрицей порядка n. В квадратной матрице А элементы a 11 , a 22 , … ann образуют главную диагональ матрицы. Другая большая диагональ a 1 n, a 2, n -1 , … an 1 называется побочной диагональю. Если все элементы квадратной матрицы, кроме элементов главной диагонали, равны нулю, то матрица называется диагональной. ►Пример 1.1. Если у диагональной матрицы все элементы, лежащие н а г л а в н о й диагонали, равны единице, то матрица называется единичной и обозначается буквой Е (в ряде книг можно встретить обозначение I). Порядок единичной матрицы обычно определяется порядком матриц, с которыми производятся операции. ►Пример 1.2.
Если в квадратной матрице все элементы, расположенные выше или ниже главной диагонали, равны нулю, то такая матрица называется треугольной. ►Пример 1.3. Здесь А и В — треугольные матрицы. ►
Если в квадратной матрице симметричные элементы относительно главной диагонали равны, т.е. aij = aji, то матрица называется симметрической. ►Пример 1.4. Элемент строки матрицы любой размерности называется крайним, если он отличен от нуля, а все элементы этой строки, находящиеся левее него, равны нулю. Матрица называется ступенчатой, если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки. ►Пример 1.5. Здесь крайний элемент каждой строки матрицы подчеркнут
Если все элементы матрицы равны нулю, то такая матрица называется нулевой и обозначается обычно буквой О. ►Пример 1.6. Нулевая матрица Две матрицы называются равными тогда и только тогда, когда они одинаковой размерности и все элементы с одинаковыми адресами этих матриц равны.
|


 и читают: «размерность m на n». Но это не значит, что размерность матрицы представляет собой обычное произведение
и читают: «размерность m на n». Но это не значит, что размерность матрицы представляет собой обычное произведение  , которое равно количеству элементов матрицы.
, которое равно количеству элементов матрицы. .
. или
или 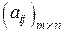 .
. — диагональная матрица. ►
— диагональная матрица. ► — единичная матрица 3-го порядка;
— единичная матрица 3-го порядка; — единичная матрица 2-го порядка. ►
— единичная матрица 2-го порядка. ► ;
;  .
. — симметрическая матрица. ►
— симметрическая матрица. ► . ►;
. ►; . ►
. ►


