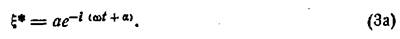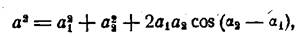Представление колебательных процессов с помощью комплексных чисел.

Представление колебательных процессов с помощью комплексных чисел.

 

Из теории комплексных чисел известно, что комплексное число ξ = ae^iφ, где а и φ — вещественные числа, е — основание натуральных логарифмов, i = √-1, может быть представлено в виде a(cos φ + i sin φ). Таким образом,

Отсюда, вещественная часть комплексного числа ξ, которую мы обозначим | ξ |, выразится следующим образом:

 

Так как последнее соотношение носит характер тождества, то, следовательно, всегда, вместо тригонометрической функции a cos(φ).мы можем рассматривать вещественную часть комплексного числа ξ = ae^iφ. Сама по себе такая замена вполне формальна и ничего нового не дает. Но дело заключается в следующем: если мы проделаем над рядом комплексных чисел ξ определенные математические действия (сложение, вычитание, умножение, дифференцирование, интегрирование и т. д.), а затем отделим вещественную часть от мнимой, то получим тот же результат, как если бы проделывали аналогичные действия над соответственными тригонометрическими функциями. Это обстоятельство позволяет заменять сравнительно громоздкие тригонометрические преобразования гораздо более простыми действиями над показательными функциями. Таким образом, пользование показательными функциями с мнимыми показателями степени, вместо соответственных тригонометрических функций, представляет с вычислительной точки зрения большие удобства.

Как мы видели, выражение вида

изображает гармоническое колебательное движение с амплитудой а, циклической частотой ω и начальной фазой α; величина t есть время, отсчитанное от некоторого начального момента.

На основании сказанного ясно, что то же гармоническое колебательное движение может быть представлено как вещественная часть | ξ | комплексного числа

При решении многих задач достаточно знать квадрат амплитуды, т. е. величину а², так как энергия колебаний пропорциональна а²; знание начальной фазы α при этом может не представлять интереса. Легко показать, что для нахождения а² нет необходимости фактически отделять в комплексном числе вида (3) вещественную часть от мнимой, а достаточно составить выражение ξ ξ*, где ξ* — комплексное число, сопряженное с ξ. (Напомним, что сопряженным комплексным числом называется число, получаемое из данного переменой знаков у всех мнимых единиц i). В самом деле, комплексное число, сопряженное с ξ, выраженным формулой (3), будет:

Составив выражение ξ ξ*, получим

 

т. е. ξ ξ* дает нам непосредственно квадрат амплитуды.

 

Обобщая выражение (3), можно и величину а положить комплексной; в этом случае она не будет, конечно, непосредственно выражать действительную амплитуду колебаний, так как действительная амплитуда всегда вещественна.

Выясним, прежде всего, какой физический смысл имеет такая „комплексная амплитуда". Для этого положим a = a₀e^{i α0}, где a₀ и α₀ — вещественные, тогда

Отделяя вещественную часть от мнимой, получим

 

откуда видно, что | ξ | представляет собою гармоническое колебательное движение с амплитудой а₀ и начальной фазой α + α₀. Таким образом, комплексное значение амплитуды означает изменение начальной фазы на а₀. Легко убедиться, что и в этом случае ξξ* дает квадрат вещественной амплитуды: ξ ξ* = а₀².

Чтобы выяснить удобство пользования комплексными числами для изображения гармонических колебательных движений, рассмотрим задачу о сложении двух гармонических колебаний x₁ = a₁ cos (ω t + α₁) и x₂ = a₂ cos (ω t + α₂) одинаковой частоты ω и происходящих вдоль одной и той же прямой. Через тригонометрические функции требуются довольно сложные преобразования. Пользуясь же комплексными числами, получим

Результирующее колебание:

Квадрат его амплитуды а² получим, умножив правую часть на величину, с ней сопряженную:

 

откуда

 

но по формуле (1)

 

откуда