Лекции по методологии социологических исследованийй 13 страница
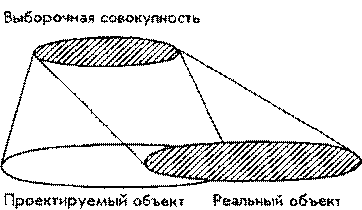
Установим три группы социологических переменных: а) переменные, не обнаруживающие динамики; б) переменные с прогнозируемой динамикой; в) переменные с непрогнозируемой динамикой. В первом случае временным смещением объекта при проектировании выборки можно пренебречь, во втором случае результаты наблюдений должны экстраполироваться на проектируемый объект с некоторым упреждением - примерно так, как производится стрельба по движущейся цели (рис. 5.1).
Рис. 5.1. Смещение реального объекта выборки относительно проектируемого объекта по времени. Надо “накрыть” генеральную совокупность, но “накрыть” ее в том месте, где она появится через определенное время. Поскольку траектории социологических переменных изучены слабо - повторные и продолжающиеся исследования трудоемки и встречаются сравнительно редко - подобные экстраполяции выборки производятся эвристически, “на глаз”, но даже в таком случае полезно фиксировать прогноз динамики переменной хотя бы в терминах “возрастет”, “снизится”, “будет колебаться”. Образцовым остается исследование Б. Берельсона, П. Лазарсфельда и В. Макфи - они установили циклы электоральных предпочтений американцев в предвыборные месяцы и даже недели. Зависимость распределения времени различных социальных и возрастных групп от будних и выходных дней, летних и зимних месяцев изучалась десятки раз, и в данном случае есть все основания говорить о хорошо прогнозируемых процессах. Часто в социологических исследованиях динамика переменных остается непрогнозируемой и выборки в данном случае имеют эпизодический характер - т. е. сама выборка являет собой не более чем эпизод. Обычно данные о субъективных и тому подобных эфемерных и ситуативных признаках привязаны к определенному периоду и за его пределами теряют смысл. Например, “рейтинг популярности” политического лидера сохраняется как факт массового сознания недолго. Мирская молва - морская волна. Примерно то же самое - реакция публики на телепередачи либо политические события. В данном случае мы имеем дело с исследованием-однодневной. Его результаты должны появиться завтра на газетной полосе и тут же устареть. Аналогичная ситуация складывается в маркетинге - экспозиция рекламного “паттерна” требует немедленного анализа и прослеживания его влияния на сознание потенциальных покупателей, пока “паттерн” не потеряет свою эффективность. Обычно “моментные” выборки применяются в тех областях социологии, которые ориентированы не на концептуальные результаты, а на внешнего заказчика и выполняют “обслуживающие” функции. Третий тип систематических ошибок - недостаточный учет аномальных и труднодоступных единиц исследования. Речь идет о тех, кто в силу обстоятельств имеет меньшую вероятность попасть в выборку. Если первый тип систематической ошибки связан с давлением доступных единиц, в данном случае причину ошибки можно обозначить как ненавязчивость малодоступных единиц. Их мало, и социолог уже на стадии проектирования генеральной совокупности должен решить, стоит ли пренебрегать малочисленными группами лиц, лишенных свободы, не имеющих определенного места жительства, работающих в отрыве от дома и т. п. Если учет малодоступных единиц не имеет существенного значения для исследования (в большинстве случаев бывает именно так), следует указать, что они исключены из выборочной совокупности. К малодоступным единицам относятся также больные, в частности, находящиеся в стационарах, очень нелегко получить возможность обследовать личный состав Вооруженных Сил (здесь может заключаться источник серьезных систематических ошибок). Меньшие шансы на попадание в выборку имеют те, кого нет дома, и отказывающиеся сотрудничать с интервьюером. Недостаточный учет отсутствующих в месте сбора данных, как правило, по месту проживания, - четвертый тип систематических ошибок. Казалось бы, не оказаться дома в момент посещения интервьюера может любой человек (канон полевого исследования требует, как минимум, троекратного посещения). На самом деле, отсутствуют дома вполне определенные контингента населения. По данным Н.Н. Чурилова, при первом посещении интервьюерам удается опросить большую часть женщин и меньше половины мужчин; при трехкратных посещениях обнаруживается, что в числе 4 - 7% труднодоступных респондентов также преобладают женщины. Среди рабочих труднодоступных респондентов 5%, среди служащих - 8%. Чем моложе респонденты, тем больше вероятность опросить их при первом визите интервьюера. С увеличением возраста респондентов увеличивается доля труднодоступных - это противоречит распространенному мнению, будто люди старшего возраста менее мобильны, чем остальные группы населения. Наиболее доступны респонденты, никогда не состоявшие в браке, - после трехкратных визитов интервьюеров доля опрошенных составила 99-100%. Пятый тип систематических ошибок - отказы от ответа, которые в зависимости от темы опроса могут составлять довольно значительный процент запланированных интервью. Особенно часто отказы от ответа наблюдаются в крупных городах. Проблема заключается в том, что в отличие от отсутствующих дома отказывающиеся отвечать, по данным исследований, существенно отличаются от сотрудничающих с интервьюером. В частности, имеющие высокое образование и информированные респонденты склонны говорить “не знаю” в противоположность малограмотным и самоуверенным, у которых есть ответ на любой вопрос. [ Бутенко И.А. “ Нет ответа”: Анализ методической ситуации на страницах журнала “Public opinion quarterly” // Социологические исследования. 1986. № 4. С. 118- 122.] Среди причин отказа от ответа можно указать три наиболее важных. Первая причина связана с содержанием вопросов, недостаточной осведомленностью респондента в предмете обсуждения либо нежеланием говорить на определенные темы. Некоторые исследуемые социологом переменные не реагируют на смещение выборочной совокупности, связанное с отказом отвечать на вопросы, другие более чувствительны. Например, беседа с интервьюером по вопросам интимной жизни вызывает затруднение у многих респондентов. В период перестройки (вторая половина 1980-х гг.), когда советские социологи увлекались “острыми” вопросами, трудящиеся старались воздерживаться от ответа или обнаруживали малую осведомленность в актуальных политических темах. Например, многие не могли сказать, как относятся к диссидентам, поскольку они ассоциировались и с пьяницами, и лицами без определенного места жительства. С другой стороны, респонденты активно отвечали на вопросы, о которых не имели представления. Н.А. Клюшина показала, что высокий процент не ответивших в некоторых случаях свидетельствует о качественной информации. По ее данным, включение вопросовфильтров при обсуждении проблем внутренней политики приводит к увеличению числа неответивших на 11% и при обсуждении внешней политики - на 1б%. Вторая причина - нежелание отвечать в силу недоброжелательной установки по отношению к интервьюеру либо такого рода опросам вообще. Этот аспект изучен недостаточно. Каких-либо систематизированных наблюдений не имеется, хотя в литературе отмечается возрастание общего количества “заисследованных досмерти” (surveyed to death) респондентов. Скорее всего это преувеличение. Наиболее способные и опытные интервьюеры умеют завоевывать доверие респондента и преодолевать его нежелание сотрудничать. Третья причина - внешние обстоятельства, препятствующие контакту, несмотря на информированность респондента и желание сотрудничать. Наиболее труднодоступными, поданным Н.Н. Чурилова, являются семейные респонденты - многие из них не могут выделить 40 - 50 мин для беседы с интервьюером, количество отказов от интервью составляет 2,5%, респонденты отсутствуют дома по известным либо неизвестным причинам в 5,2% случаев”. По данным опроса 395 молодых рабочих в 1982 г. в Киеве, несостоявшиеся интервью связаны с отпуском респондента (0,4%), болезнью (0,4%), отказом от опроса (3,2%), декретным отпуском (3,6%), призывом в армию (1,2%), увольнением с места работы (2,0%). Другие причины отсутствия ответов обусловлены утерей анкет, отказом вернуть заполненные анкеты и т. п. Общая величина систематической ошибки, как показал Н.Н. Чурилов, составляет 3,03%, что существенно не влияет на выборочную среднюю. Уровень систематической ошибки можно несколько снизить заменой отсутствующих либо отказавшихся отвечать респондентов лицами из резервного контингента, но самым надежным способом реализации выборки являются повторные посещения. Однократное посещение обеспечивает опрос примерно 55% респондентов, второе и третье посещения увеличивают это число до 95 - 9б%. Повторные посещения респондентов, отсутствующих дома, обходятся довольно дорого. Поэтому в 1950-е гг. в Институте Гэллапа была разработана система интервьюирования, названная “Время-Место”. Было проведено специальное исследование и установлено: кто, когда с наибольшей вероятностью находится дома. Естественно, что опросы обычно проводятся в вечернее время и в выходные дни. Общее количество отказов варьирует от 5% в переписях населения США до 30% в отдельных “трудных” обследованиях, например касающихся доходов или интимной жизни. Особенно много отказов в крупных городах. Менее всего расположены к сотрудничеству с интервьюером белые и высокообразованные люди. Возможно, увеличение отказов в последние годы обусловлено соображениями безопасности. Определенную роль играет и снижение уровня подготовки интервьюеров, которые в большинстве случаев рассматривают это ремесло как временную подработку”. Вряд ли возможно предвидеть все систематические ошибки, встречающиеся в массовых опросах. Например, в исследовании воспроизводства трудовых ресурсов Киева в 1984г. применялся отбор респондентов по избирательным спискам - выписывался адрес каждого сотого избирателя. В.И. Паниотто заметил, что, если начинать отбор по алфавитному списку, получат преимущество респонденты, фамилия которых начинается на букву “ А”. Возникнет систематическая ошибка: в частности, большие шансы на то, чтобы попасть в выборку в Киеве, получат армяне, поскольку их фамилии часто начинаются на “А”. Чтобы избежать этого, В.И. Паниотто начинал отбор в каждом списке с номера, равного целой части числа к/7 + 6/7, где к - номер избирательного участка, изменяющийся от 1 до 700. Каковы способы отбора единиц исследования? Н.Н. Чурилов выделяет сплошной, случайный и неслучайный способы отбора единиц исследования. К случайной выборке он относит выборку вероятностную, систематическую, районированную и гнездовую. Неслучайные методы отбора-“стихийная” выборка, квотная выборка и метод “основного массива”. Если генеральная совокупность имеет небольшой объем и можно обеспечить равную вероятность отбора каждой единицы исследования, применяется вероятностная выборка. Это не просто случайный бессистемный отбор, а строгая процедура, чаще всего основанная на использовании таблицы случайных чисел. Такого рода процедуру можно использовать только в том случае, если единицы исследования удается пронумеровать. Однако чаще всего приходится разделять обследуемую совокупность на более или менее однородные части и затем осуществлять отбор единиц внутри этих частей. Такое разделение совокупности на части называется районированием. Проблема заключается в обеспечении однородности выделяемых классов на основе существенных для исследователя критериев. Для решения такой задачи необходимо располагать данными о структуре генеральной совокупности и, в частности, о распределении признака районирования. Выделенные “районы” должны существенно отличаться друг от друга, но им должна быть присуща внутренняя однородность. Противоположность районированной выборке составляет выборка гнездовая, где обследуется промежуточный объект. Первоначально гнездовая выборка разрабатывалась в сельскохозяйственной статистике. В качестве социологических гнезд могут выступать населенные пункты, районы, предприятия, бригады. Реализовать такую выборку намного легче, чем вероятностную либо районированную. Единицы исследования здесь размещены компактно. Проблемы, которые возникают при гнездовом отборе, связаны с определением величины гнезда, количеством гнезд, которые надо обследовать, и их размещением в генеральной совокупности. Систематический отбор является упрощенным вариантом случайного отбора. В основу выборки здесь положены не вероятностные процедуры, а алфавитные списки, картотеки, схемы, которые, как предполагается, не зависят от изучаемого признака и обеспечивают равновероятность попадания в выборку всех единиц генеральной совокупности. Квотный отбор основан на целенаправленном формировании структуры выборочной совокупности. Интервьюер получает задание опросить некоторое количество лиц определенного возраста, пола, образования и профессии. Удельный вес квоты в выборочной совокупности должен соответствовать ее удельному весу в генеральной совокупности. Обычно квотная выборка используется на последних ступенях отбора и завершает процесс районирования и применения вероятностных процедур. Например, в штате Нью-Йорк проживает 10% населения США. Следовательно, 10% интервью должны быть проведены в Нью-Йорке. Если объем национальной выборки 10 000 человек, то на Нью-Йорк приходится 1000 интервью. Далее. НьюЙорк Сити включает 40% населения штата. Следовательно, 400 интервью будут проведены в Нью-Йорк Сити. Поскольку третья часть жителей Нью-Йорк Сити живет в Бруклине, 133 интервью будут проведены в этом районе. Кроме территориальных признаков, для определения квоты выбираются социальный статус, возраст, пол, иногда раса. Распределение этих признаков в генеральной совокупности известно и нетрудно обеспечить ее идентичность структуре выборки. Но при соблюдении квот остается много возможностей для систематических ошибок. В частности, интервьюер, разыскивая респондента определенного пола, статуса и возраста в заданном районе, предпочтет беседовать с более привлекательными и коммуникабельными людьми. Дж. Гэллап отмечал, что в квотных выборках обнаруживается слишком много людей, окончивших колледж, с доходами выше среднего, республиканцев по политическим ориентациям. Поэтому вероятностный отбор обладает немалым преимуществом перед квотным: выборка меньше зависит от инициативы интервьюера. Метод стихийного отбора внешне похож на случайный. Исследователь здесь имеет дело с максимально доступными для него единицами наблюдения и исходит по преимуществу только из критерия принадлежности респондента к проектируемой генеральной совокупности. Чаще всего в данном случае допускаются неконтролируемые систематические ошибки. Особенно это относится куличным опросам, когда фиксируется мнение тех, кто имеет возможность и желание поговорить с интервьюером. Существенную роль в данном случае играет взаимное расположение при встрече. Нередко интервьюер, получив задание провести опрос, обращается к своим знакомым. Обследования, проводимые с помощью публикуемых в газетах вопросников, строго говоря, относятся к воображаемому объекту. Оценить репрезентативность выборочных средних при стихийном отборе практически невозможно. К стихийному отбору относится и метод основного массива, преимущество которого состоит в том, что выборочная совокупность составляет значительную долю генеральной и перекрывает возможное смещение. Например, при обследовании коллектива предприятия вполне достаточно опросить “большинство” работников и это обеспечит близость выборочной и генеральной средних. 5. Теоретические основы случайного отбора Вариация выборочной средней. Центральная предельная теорема. Правило “трех сигм”. Предположим, что мы имеем дело с идеальной генеральной совокупностью, каждый элемент которой обладает абсолютно равными шансами попасть в выборку. Численность генеральной совокупности не должна быть особенно большой, чтобы не усложнять дело. Предположим, что объем нашей генеральной совокупности 5 человек. Предположим, далее, что тема нашего исследования - “затраты времени на чтение”. Значения переменной “затраты времени на чтение” устанавливаются в минутах в среднем за день. Следующее допущение еще более условно. Мы должны определить параметры каждой из единиц генеральной совокупности и вычислить средние затраты времени на чтение. В реальности, где объем генеральных совокупностей составляет обычно тысячи и миллионы единиц, такая задача социологу не по силам. Но в нашем-то примере генеральная совокупность состоит всего из пяти человек. Вернемся к примеру и предположим, что мы обладаем неким демоническим знанием о затратах времени на чтение у пяти человек (табл. 5.8). Таблица 5.8. Затраты времени на чтение, матрица данных генеральной совокупности из пяти человек
Искомая характеристика генеральной совокупности - средние затраты времени на чтение: 40 мин. Нормальные проектировщики выборки всего этого не знают - у них нет возможности обследовать всю генеральную совокупность из пяти семей - поэтому и начинают строить выборку. Допустим, что объем выборочной совокупности из 2 человек достаточен для заданного уровня надежности предсказания. Тогда мы можем начать процедуру отбора единиц исследования. Напомним, что все 5 человек имеют равные шансы быть опрошеными. Здесь не помешает и напоминание об аналогии социологического отбора со случайным процессом: как будто мы вынимаем из мешка шар и регистрируем его параметры. Поскольку объем выборки 2 человека, опросим Ивана и Павла, подсчитаем их средние затраты времени на чтение и зарегистрируем результат: 45 мин. Обследование завершено. В социологической практике опросы ограничиваются одной выборкой, а в нашем примере полезно осуществить и другие выборки из той же генеральной совокупности. Ведь кроме Ивана и Павла есть и иные единицы, имеющие такие же шансы быть обследованными. Произведем вторую выборку - опросим Ивана и Петра. Их средняя составит 15 мин. В третью выборку оба раза попал Павел - после регистрации результатов опроса единица возвращается в генеральную совокупность и может быть “вынута” вторично - такая выборка называется возвратной. Выборочная средняя “двойного” опроса Павла составляет 80 мин. Четвертый раз выпали Александр и Иосиф - средняя 45 мин. Предположим, в пятую выборку два раза вошел Иван, средняя составляет 10 мин. Мы видим, что все происходящее слишком случайно и, тем не менее, следует подсчитать ошибки выборки - разницу между значениями выборочной и генеральной совокупности по модулю (пока безразлично, какой знак имеет отклонение): Таблица 5.9. Затраты времени на чтение в пяти случайных выборках и соответствующие отклонения выборочных средних от генеральной средней, мин
Уже на этой стадии мы можем сделать некоторые важные выводы. Во-первых, мы видим, что в одной и той же генеральной совокупности можно произвести много выборок, результаты которых иногда значительно отличаются друг от друга. У нас в одной выборке средняя составила 80 мин, а в другой - 10 мин. Во-вторых, поскольку никаких специальных действий для получения определенной выборки не предпринимается и каждая выборка (пара индивидов) имеет равный шанс, можно надеяться, что выборочная средняя является случайной величиной. То обстоятельство, что случайные выборки дают столь различающиеся результаты, подозрительно, и есть основания заняться установлением всех возможных выборочных средних и, соответственно ошибок выборки. Для этого надо выписать все сочетания единиц исследования по две в генеральной совокупности из пяти единиц (вместо имен опрошенных удобнее оперировать номерами). Напомним, что отбор единиц - возвратный, т. е. каждая из них возвращается обратно в генеральную совокупность и может попасть в выборку еще и еще раз, разумеется, с такими же шансами, что и остальные единицы. Всего таких сочетаний может быть пт, где п - объем генеральной совокупности, т - объем выборки (табл. 5.10). Таблица 5.10. Все возможные выборки по 2 единицы из генеральной совокупности в 5 единиц и соответствующие им значения выборочной средней
Мы видим, что из 25 возможных выборок и соответствующих средних только одна совпала с генеральной средней. Разброс значений выборочной средней составляет от 10 до 80 мин. Отсюда видно, что выборки могут быть хорошими и плохими. Теперь мы имеем возможность оценить вероятность различных выборок. Мы видим весь диапазон вариации выборочных параметров - от 10 до 80 мин. Однако эта картина еще мало о чем говорит. Ясно одно: каждая отдельная выборка в той или иной степени далека от “истинной” - генеральной - средней. Вместе с тем нетрудно заметить, что из 25 выборок одни встречаются редко, а другие часто. Дальнейшая задача заключается в том, чтобы организовать совокупность выборок и найти в ней внутреннюю логику. Речь идет уже не о выборочных совокупностях (у нас они включают по две единицы), а о совокупности выборок. Ее объем составляет 25 единиц. Просмотрим правую колонку табл. 5.10 сверху вниз и сгруппируем значения выборочных средних в порядке их возрастания: 10, 15, 15, 20, 25, 25, 30, 30, 30, 30, 35, 35, 40, 45, 45, 45, 45, 50, 50, 50, 60, 60, 65, 65, 80. Здесь уже можно видеть, что “срединные” выборочные средние встречаются чаще, чем “крайние”. Эта важная особенность распределения выборочных средних становится особенно отчетливой, если мы подсчитаем для каждого значения выборочной средней частоту, с которой она встречается среди всех 25 выборок (табл. 5.11). Таблица 5.11. Частотное распределение всех выборочных средних затрат времени на чтение в генеральной совокупности из пяти единиц, условный пример
Удивительно: несмотря на то что частотное распределение стремится к своему центру тяжести, “истинное” значение исследуемой переменной встретилось в наших 25 выборках только один раз. Однако продолжим расчеты и вычислим среднюю величину всех выборочных значений. Если вспомнить о том, что выборочное значение само представляет собой среднюю величину, задача формулируется более точно: подсчитаем среднюю всех выборочных средних. Это можно сделать в ранжированном ряду выборочных средних, который мы построили, но лучше исчислить средневзвешенную величину: умножить каждое значение переменной на его частоту, сложить произведения, а полученную сумму разделить на общее число наблюдений. Здесь мы подходим к важному статистическому открытию, которое называется центральной предельной теоремой. Его суть заключается в том, что средняя всех возможных выборочных средних равна генеральной средней. Действительно, подсчитав среднюю всех средних, мы получим Сама по себе центральная предельная теорема малопрактична, поскольку произвести все выборки из генеральной совокупности несоизмеримо труднее, чем обследовать всю генеральную совокупность. В нашем примере генеральная совокупность составляет 5 человек, а выборок - 25. Если генеральная совокупность достаточно многочисленна, отдельные выборки остаются единственным средством приближения к генеральной средней. У нас каждая выборка, за исключением одной, показывающей истинное значение 40 мин, характеризуется некоторой ошибкой, и вероятность этой ошибки, равно как и вероятность точного попадания в середину, может быть исчислена путем деления частоты i -й выборки на число всех выборок. Мы знаем генеральную среднюю в пяти наблюдениях и сейчас имеем возможность рассчитать вероятность “попадания” в среднюю каждого отдельного наблюдения. Это 1/5, или 20%. Вероятность того, что выборка из двух единиц покажет значение, равное генеральной средней, - 1/25 (1/5х1/5), или 4%. Если бы мы производили отбор трех человек из пяти, вероятность построения “точной” выборки равнялась бы 1/125 (1/5 х 1/5х 1/5), или 0,16%. Но в данном случае и количество всех возможных выборок равнялось бы 53 = 125. Итак, точное “попадание” в генеральную среднюю маловероятно, но следующий шаг заключается в том, чтобы узнать, каково среднее отклонение от выборочной средней. Для этого нам понадобится показатель среднего квадратического отклонения:
Сейчас мы располагаем всеми данными для расчета среднего квадратического отклонения: 17,32 мин. Величина среднего квадратического отклонения позволяет заранее предсказать, какое количество выборок в данной генеральной совокупности будут “плохими”, т. е. отклонятся от средней на слишком большое расстояние, а сколько из них дадут приемлемые значения. Иными словами, ошибка выборки при условии, что она случайна, поддается априорному расчету. В нашем примере выборка (два человека из совокупности в пять человек) слишком мала, чтобы пытаться установить в ней какую-либо регулярность. Но сотни и тысячи случайных выборок, точнее, параметры случайных выборок, распределяются в соответствии с законом, который называется законом нормального распределения. Его суть заключается в том, что наибольшее число выборочных средних располагается в середине ряда плотности распределения, а крайние значения маловероятны. Чем больше число наблюдений, тем ближе распределение выборочных средних к нормальной кривой. Это дает возможность опираться на законы вероятностей и прогнозировать надежность выборочных наблюдений. При идеальном случайном отборе в пределах одного среднего квадратического отклонения варьируют результаты 68,27% всех возможных выборок, в пределах двух средних квадратических отклонений - 95,45%, а в пределах трех “сигм” - 99,73%. Это означает, что при достаточно большом числе замеров в среднем из каждых 1000 выборок 683 дадут значения, не выходящие за пределы одной “сигмы”, 954 не выйдут за пределы двух “сигм”, а 997 - за пределы трех “сигм”. Это означает также, что при любой выборке есть риск ошибиться. В среднем лишь в трех выборках из 1000 ошибка будет больше заданных значений. Увеличим точность приближения к средней всех выборочных средних до двух “сигм”, и риск ошибиться возрастет до 46 случаев из 1000; за пределы одного среднего квадратического отклонения выйдут 317 выборок из 1000 (рис. 5.2). “Правило трех сигм” позволяет заранее оценить вероятность ошибки случайной выборки. Чем выше требования к точности, тем выше риск ошибки и соответственно ниже вероятность правильного ответа. Вообще, выборка аналогична стрельбе в цель: чем больше по размеру мишень, тем выше вероятность попадания. Если сделать 1000 выстрелов из оружия, прицел которого установлен правильно, 683 выстрела будут удачными в том смысле, что не выйдут за пределы одной “сигмы”.
|

 (табл. 5.9)
(табл. 5.9)
 = 40 мин. И что бы мы ни взяли и качестве предмета выборочного обследования, всегда случайные выборки будут распределяться вокруг генеральной средней.
= 40 мин. И что бы мы ни взяли и качестве предмета выборочного обследования, всегда случайные выборки будут распределяться вокруг генеральной средней. , где х1 - i-я выборочная средняя, х ср - средняя всех выборочных средних, pi -число наблюдений.
, где х1 - i-я выборочная средняя, х ср - средняя всех выборочных средних, pi -число наблюдений.


