Лекции по методологии социологических исследованийй 14 страница“Правило трех сигм” действует применительно к случайным процессам - выпадениям правильного “кубика”, монетки, шарам. Но мы знаем, что и вариация выборочной средней является случайным процессом: средняя всех выборочных средних в точности равна генеральной средней, а среднее квадратическое отклонение тоже известно. Поэтому в любом ряду распределения можно установить пределы, в которых находятся выборочные средние с вероятностью 683 из 1000; 954 из 1000 и 997 из 1000. Вернемся к условному примеру, где производилась выборка из двух человек в генеральной совокупности из пяти человек. Средние затраты времени на чтение составили в 25 выборках 40 мин. Среднее квадратическое отклонение 17,3 мин. Сейчас мы можем подсчитать область распределения, соответствующую одному среднему квадратическому отклонению: нижний предел 40 мин. - 17,3 мин = 22,7 мин; верхний предел 40 мин + 17,3 мин = 57,3 мин. Какие из 25 выборочных средних попадают в этот интервал? Посмотрим табл. 5.11 и увидим, что в интервале от 22,7 мин до 57,3 мин имеются значения 25 мин - две выборки, 30 мин -четыре выборки, 35 мин - две выборки, 40 мин - одна выборка, 45 мин - четыре выборки и 50 мин - три выборки. Общей сложностью насчитывается 16 выборок из 25 (2+4+2+1+4+3). Переведем эту цифру в проценты и получим 64 - такова вероятность, что наша случайная выборка не выйдет за пределы одного среднего квадратического отклонения. Расхождение с одной “сигмой” обусловлено малочисленностью наблюдений.
Рис. 5.2. Распределение выборочных средних Удвоенное среднее квадратическое отклонение равно 17,3 х 2 = 34,6 мин. Нижняя граница интервала составляет в данном случае 40 - 34,6 = 5,4 мин; верхняя граница: 40 + 34,6 = 74,6 мин. Из всех наших выборок только одна (80 мин.) вышла из этих пределов, а 24 уместились в две “сигмы”. В нормальном распределении данный интервал включает 95,4% выборок. У нас таких 96%. Утроенное среднее отклонение охватит в нашем условном примере все выборочные средние. В реальности же три из 1000 случайных выборок выйдут за пределы “трех сигм”. Производя выборку, исследователь не имеет возможности установить ее среднее квадратическое отклонение-для этого понадобилось бы анализировать все выборочные средние. Приходится использовать установленное теорией соотношение между средним квадратическим отклонением выборочных средних и средним квадратическим отклонением генеральной совокупности Очевидно, чем больше объем выборки, тем меньше вариация выборочных средних. Проверим это соотношение на нашем условном примере: установим среднее квадратическое отклонение затрат времени на чтение у пяти человек (табл. 5.13). Таблица 5.13. Расчет среднего квадратического отклонения в генеральной совокупности из пяти человек
У нас есть возможность вычислить среднее квадратическое отклонение генеральной совокупности muген =24,5 мин. Теперь, узнав среднее квадратическое отклонение генеральной совокупности, мы можем вычислить среднее квадратическое отклонение выборочных средних sigmaген = 17,32 мин. Это соотношение, устанавливающее прямо пропорциональную зависимость средней ошибки выборки от среднего квадратического отклонения генеральной совокупности и обратно пропорциональную зависимость от корня квадратного из величины выборочной совокупности, позволяет не производить сотни и тысячи выборок. Ошибка выборки рассчитывается на основе сведений об однородности генеральной совокупности, а также об объеме выборки. Вернемся к нашему примеру с затратами времени на чтение. Мы знаем среднее значение изучаемой переменной в генеральной совокупности - 40 мин. - и ее среднее квадратическое отклонение - 24,52 мин. Средняя ошибка выборки объемом в две единицы равна 17,32 мин. Это означает, что из 1000 выборок 683 дадут результаты от 22,68 мин. (40 - 17,32) до 57,32 мин. (40 + 17,32). Если бы выборка состояла из трех человек, ее ожидаемая ошибка была бы поменьше: 14,14 мин. В данном случае с такой же вероятностью в 683 из 1000 мы можем утверждать, что результат выборочного наблюдения не будет ниже 25,86 мин и выше 54,14 мин. Выборка из четырех человек еще больше повысит точность предсказания: 12,25 мин. Интервал среднего отклонения от истинного значения признака уменьшился: от 27,75 мин. до 52,25 мин. Таким образом, величина средней ошибки выборки, т. е. средняя всех отклонений выборочной средней от общей средней, зависит от двух параметров: от степени однородности распределения изучаемого признака в генеральной совокупности и объема выборки. Представим себе, что обследуемая совокупность совершенно однородна - отклонения от средней равны нулю. Например, все респонденты имеют один и тот же возраст - вариация данного признака нулевая. Величина знаменателя в формуле для "мю" не имеет значения, потому что, даже если выборка будет состоять из одного-единственного наблюдения, ошибка останется нулевой. При разнородной генеральной совокупности ошибка выборки уменьшается с увеличением ее объема. Если объем выборки приближается к объему генеральной совокупности, ошибка стремится к нулю. Задача исчисления ошибки выборки сводится к определению вероятности того или иного варианта. В нашем примере выборочного наблюдения двух человек из пяти вероятность выборочного значения 40 мин, равно как и прочих, равна 0,04. Но вероятность установления значений от 35 до 45 мин. возрастает: 0,04 + 0,08 + 0,16 = 0,28 - это хорошо видно в табл. 5.11. Чем меньше точность, тем выше надежность выборочных данных. “Сигмы” имеют в каждом конкретном случае разную размерность: минуты, белые и черные шары, метры, баллы. Метры и минуты нельзя сопоставить друг с другом. Поэтому целесообразно нормировать отклонения выборочной средней путем введения относительной величины: Величина t показывает, в каком отношении находится средняя ошибка выборки к одному среднему квадратическому отклонению. Аналогия со стрельбами в данном случае не покажется лишней. Чем меньше размер цели, тем меньше уверенность в попадании. При t = 1 отклонение выборочной средней от генеральной равно одной “сигме” и, как мы знаем, вероятность такого варианта равняется 683 случаям из 1000, т. е. 0,683. При снижении точности предсказания в два раза, т. е. при t = 2, вероятность возрастает до 0,954, при t = 3 - до 0,997, при t = 4 - до 0,999. Используя коэффициент t, мы можем ввести определение предельной ошибки выборки "мю". Предельная ошибка выборки непосредственно зависит от принятого нами уровня точности - коэффициента t. е = t х. Если мы не хотим ошибиться в своих заключениях, надо увеличить t, при t = 4 вероятность того, что выборочная средняя не выйдет за пределы четырех средних отклонений, составит 0,999. Расчет средней ошибки выборки, как было показано выше, зависит от однородности генеральной совокупности - мюген. Новыборка производится как раз для того, чтобы установить параметры генеральной совокупности. Поэтому практического смысла формула Рассмотрим частотное распределение выборочной совокупности 807 школьников по количеству имевшихся у них наличных денег (табл. 5.14). Прежде всего необходимо подсчитать среднюю арифметическую где х - значения переменной, р - частоты. Среднее количество Таблица 5.14 Распределение школьников по количеству имевшихся у них наличных денег, 1987 г., %
Вывод: с вероятностью 0,997 можно утверждать, что среднее количество денег у советских школьников в 1987 г. составляло от 41,1 до 48,9 руб. Если этот вывод не устраивает нас из-за своей приблизительности, мы имеем возможность повысить точность предельной ошибки, например, принять t = 1. Тогда с = 1,3 руб. Интервал сокращается: нижний предел составляет 45 - 1,3 = 43,7 руб; верхний предел 45 + 1,3 = 46,3 руб. Утверждать, что генеральная средняя будет находиться в установленных таким образом пределах, мы можем с вероятностью 0,683. Это значит, что мы ошибемся в 317 случаях из 1000. Выборка должна быть достаточно большой, но, как мы знаем из опыта, ее объем выше определенного предела расширять нецелесообразно - на точность результата это уже не влияет. Поэтому прежде всего требуется определить точность предстоящего измерения. Вряд ли нужно измерять сумму наличных денег с точностью до рубля или затраты времени с точностью до минуты. Если требуются самые высокие гарантии и самая точная информация, выборка должна быть большой. Кроме точности и надежности результатов выборочного наблюдения, на объем выборки влияет независимый от исследователя фактор - степень однородности генеральной совокупности. В однородной совокупности не нужны многократно повторяющиеся замеры. Представим три фактора, влияющие на объем выборки, в формальном виде. Греческая буква "мю" обозначает заданную точность - предельную ошибку выборки; t - коэффициент, обозначающий заданную надежность предсказания генеральной средней, - обычно устанавливается вероятность 0,997, t = 3; степень однородности генеральной совокупности измеряется средним квадратическим отклонением deltaген. Средняя ошибка выборки Часто при измерении социологических признаков приходится оперировать долями. В этом случае формула видоизменяется. Средняя ошибка для выборочной доли равна Б.Ц. Урланис приводит следующий пример. Производится обследование студентов по полу. Предельная ошибка выборки (точность) устанавливается 2 процента (0,02). Надежность t = 3, т. е. в 997 случаях из 1000 генеральная средняя попадет в требуемый интервал. В итоге вычисляется объем выборки:
Исходя из возможноймаксимальной вариации признака в генеральной совокупности В.И. Паниотто рекомендует следующие объемы выборочной совокупности в зависимости от величины генеральной совокупности (при допущении, что с вероятностью 0,954 генеральная средняя попадает в интервал Таблица 5.15 Соотношение объемов выборочной и генеральной совокупностей при Р = 0,954 и ошибке 5%
Таким образом, для выборки с пятипроцентной ошибкой достаточно обследовать 400 единиц при практически бесконечной генеральной совокупности и уровне надежности 95%. Повышение требований к точности предсказания до 4% при сохранении прочих условий увеличивает объем выборки до 625 единиц, точность 3% предполагает объем 1111 единиц, 2% - 2500 единиц и 1% - 10 000 единиц. Фактически объем выборки зависит не столько от величины генеральной совокупности и допустимой ошибки, сколько от количества градаций, используемых при анализе массива. Для часто используемых в социологии двумерных распределений основную роль играет значимость различий между долями изучаемого признака при сравнении двух совпадающих по численности групп респондентов, выбранных случайным образом из бесконечной генеральной совокупности. Например, различия в 10% не случайны с вероятностью 0,954, если сравниваются группы по 200 человек. Двухпроцентные различия не случайны с той же вероятностью при сравнении пятитысячных групп (табл. 5.16). Таблица 5.16. Зависимость численности сравниваемых групп от значимости различий при Р=0,954, %
Таким образом, увеличение выборочной совокупности необходимо лишь для статистически корректного анализа межгрупповых различий. Вопросы 1. Что такое “концептуальный объект” и чем он отличается от генеральной совокупности? 2. Почему в социологических исследованиях ошибку выборки, как правило, приходится оценивать косвенными методами? 3. Что такое метод апостериорного контроля репрезентативности и какие признаки используются для оценки репрезентативности в массовых опросах ВЦИОМ? 4. Почему случайные ошибки выборки уменьшаются при возрастании объема выборочной совокупности, а систематические ошибки возрастают? 5. При каких условиях маленькая выборка может быть более репрезентативна, чем большая? 6. Какие систематические ошибки были допущены при проектировании опроса избирателей журналом “Литерэри Дайджест” в 1936 г.? 7. Каковы возможные причины существенных различий между данными предвыборных опросов и результатами голосования на выборах в Федеральное собрание России в декабре 1993 г.? 8. Какие систематические ошибки связаны с фактором временных изменений объекта? 9. Какие единицы исследования принято считать труднодоступными? 10. Каковы типичные причины отказа от ответа? 11. Что обычно предпринимается для ремонта выборки? 12. Каковы основные способы вероятностного отбора единиц? 13. Какова техника квотного отбора? 14. Сколько выборок можно произвести в одной и той же генеральной совокупности? 15. Как распределена выборочная средняя? 16. Почему средняя всех возможных выборочных средних в точности равна генеральной средней? 17. Сколько случайных выборок находится в пределах одного, двух и трех средних квадратических отклонений? 18. От чего зависит объем выборочной совокупности? 19. Что такое точность и заданная надежность предсказания выборочного оценивания? ЛИТЕРАТУРА 1. Вейнберг Дж., Шумекер Дж. Статистика. М.: Финансы и статистика, 1979. 2. Кимбл Г. Как правильно пользоваться статистикой. М.: Финансы и статистика, 1982. 3. Королев Ю. Т. Выборочный метод в социологии. М.: Финансы и статистика, 1975. 4. Территориальная выборка d социологических исследованиях/ И. Б. Мучник и др.; Отв. ред. Т.В. Рябушкин. М.: Наука, 1980. 5. Чурилов Н. Н. Проектирование выборочного социологического исследования. Киев: Наукова думка, 1986. Глава 6. Экспериментальный метод в социологии 1. Схема эксперимента Для чего нужна контрольная группа? Три способа выравнивания контрольной и экспериментальной групп. Задачи, решаемые экспериментом: сравнение, манипулирование, контроль, генерализация. Три условия экспериментального вывода: временная последовательность, ковариация, контроль “третьего” фактора. Определения внутренней и внешней валидности. Типичные нарушения внешней валидности: отсутствие репрезентативности и искусственно созданная экспериментальная ситуация. Всякое человеческое действие, предпринятое для достижения определенного результата, - это эксперимент, более или менее успешный. Задача науки заключается в том, чтобы установить точные правила экспериментирования и применять их для достижения заданных параметров. Объектом эксперимента для социолога являются люди и социальные общности - часто их реакция на “научное” вмешательство оказывается непредсказуемой, во всяком случае для экспериментатора. Логика экспериментального метода была разработана английским социологом и моралистом Джоном Стюартом Миллем, жившим в XIX в. Милль установил пять логических схем индуктивного вывода, одна из которых - “метод различия” - являет собой классическую схему эксперимента. Схема эта довольно проста. Сначала берутся две совокупности (два объекта) и выравниваются по значимым признакам. Иначе говоря, нужно сделать так, чтобы группы практически не различались. Конечно, они не могут не различаться вовсе. Поэтому внимание экспериментатора сосредоточивается на значимых признаках, т. е. на тех, которые могут оказать влияние на результаты эксперимента. Например, изучая воздействие телепередачи на политические установки зрителей, исследователь должен убедиться, что возраст испытуемых в различных группах варьирует незначительно. Почему возраст? Потому что из предшествующих исследований известно, что возраст влияет на политические установки. Следовательно, этот признак подлежит контролю. Несколько по-иному оценивается, например, численность блондинов, брюнетов или шатенов. Обычно такого рода параметрами при изучении политических установок пренебрегают, почему-то не считая их значимыми. Чем больше параметров учитывает исследователь, тем надежнее эксперимент. Затем начинается полевой или лабораторный этап эксперимента. Иногда утверждается, что это самый главный этап - собственно эксперимент. Такое суждение опрометчиво. Успех или провал эксперимента зависит прежде всего от того, насколько тщательно проработаны его идеальная схема, план проведения и ожидаемые результаты. Лабораторное (полевое) исследование не должно сталкиваться с “нештатными” ситуациями, т. е. ситуациями, не предусмотренными предварительно разработанным планом. Если это происходит, полевую работу надо немедленно прекратить и вернуться к проектированию исследования. Неудача исследования заключается отнюдь не в отрицательном результате - иногда он имеет большее значение, чем Положительный, - а в получении ничего не означающих данных. Предположим, что все идет “штатно” и мы находимся на полевом этапе эксперимента. Здесь одна группа объектов подвергается воздействию экспериментальной переменной. Все, кто работает в “опытных” науках, делают примерно одно и то же. Химик подвергает вещество воздействию реактива и затем наблюдает, как оно меняет цвет. Физик нагревает газы с целью продемонстрировать их расширение при нагревании. Агробиолог охлаждает семена и затем фиксирует динамику роста яровых (правда, потом это оказывается ошибкой). Социолог показывает студентам учебный фильм и констатирует усвоение материала. На этом эксперимент не заканчивается. Чтобы убедиться в том, что данные результаты возникли вследствие воздействия именно экспериментальной переменной, а не какой-либо иной, следует сопоставить параметры экспериментальной группы с параметрами группы, где никаких воздействий не применялось. Различие между этими параметрами и есть результат воздействия экспериментальной переменной. Если различие нулевое или несущественное, мы констатируем отсутствие связи. Если применение экспериментальной переменной значительно изменяет распределение изучаемого признака, имеются основания предполагать причинную связь между ними. Такова общая схема, которая лежит в основании более сложных планов эксперимента. Классический проект проверки гипотез предполагает работу с двумя объектами: экспериментальным и контрольным. Это не значит, что все экспериментаторы обязаны работать с двумя объектами. Естественные науки XIX в. не знали такого разделения объектов. Впервые экспериментальную и контрольную группы стали выделять в начале XX в. В социологии и социальной психологии в качестве объектов выбираются группы, идентичные по составу. Экспериментальной группой называется та группа, к которой “применяется” изучаемая независимая переменная; контрольная группа остается вне экспериментального воздействия. Экспериментальная и контрольная группы должны быть практически идентичными. Идентичность экспериментальной и контрольной групп достигается двумя способами. Первый способ - попарное выравнивание объектов по значимым переменным, установленным до проведения экспериментальных операций. Выравнивание можно осуществить путем подбора для каждого объекта экспериментальной группы идентичного объекта в контрольной группе. Например, если в экспериментальную группу входит мужчина 40 лет с высшим гуманитарным образованием, в контрольной группе должен быть его “двойник” с такими же параметрами. Очевидно, подбор “двойников” возможен лишь при очень ограниченном числе переменных. В противном случае комплектование групп превращается в неразрешимую задачу. Второй, более доступный, метод выравнивания групп основан на выравнивании частотных распределений, а не каждой пары в отдельности. Например, экспериментатор обеспечивает 30-процентную долю испытуемых с высшим образованием и в той, и в другой группе. Аналогичные выравнивания осуществляются и по другим признакам, а отдельные испытуемые уже не контролируются. Разумеется, в данном случае не достигается высокого сходства между группами, но комплектование групп намного облегчается. Третий способ обеспечения идентичности экспериментальной и контрольной групп - случайное распределение объектов по группам. Чаще всего такой способ называют рандомизацией. В отличие от выравнивания рандомизация, как предполагается, устраняет систематические различия между группами по всем признакам, а не только контролируемым исследователем. Для осуществления рандомизации массив надо как следует перемешать и разделить равновероятно. Данный способ особенно предпочтителен в тех случаях, когда у исследователя нет уверенности, что различия между группами контролируются по значимым переменным. А такой уверенности нет никогда. Обеспечить равновероятное распределение контингента на две группы не так просто, как это кажется. Каждый объект должен иметь одинаковую вероятность попасть в экспериментальную и контрольную группы, поэтому рекомендуется осуществлять отбор с помощью таблицы случайных чисел либо жребия. Для определения эффекта, производимого экспериментальной переменной, осуществляются несколько замеров и в той, и в другой группах. Предварительный замер - претест - производится до того, как экспериментальная группа подвергнется воздействию изучаемой переменной. При этом различия между значениями зависимой переменной в контрольной и экспериментальной группах должны быть минимальными. После того как экспериментальная группа подверглась воздействию определенного стимула, осуществляются замеры в обеих группах. Если значение зависимой переменной в экспериментальной группе статистически значимо отличается от значения претеста и превышает (статистически значимо) значение претеста в контрольной группе, делается вывод (с указанием вероятности случайной ошибки), что переменная-стимул связана с переменной-реакцией. Таким образом, гипотеза принимается (как неопровергнутая, а не как подтвержденная) или опровергается. Пример экспериментальной проверки гипотезы - исследование влияния мнения учителей об интеллектуальном развитии учеников на интеллектуальное развитие учеников. Исследование проведено Р. Розенталем и Л. Джейкобсом. Экспериментаторы предположили, что ученики, способности которых оцениваются учителями более высоко, действительно обнаруживают большие успехи. Гипотеза проверялась на материале обследования учеников средней школы в районе, где жили преимущественно бедные. Все ученики прошли тестирование по уровню интеллектуальности (использовалась невербальная техника тестирования). Затем с результатами тестирования ознакомили учителей: им сообщили имена детей, обнаруживших большие способности. На самом деле имена “вундеркиндов” были выбраны случайным порядком. Таким образом, экспериментальная группа состояла из “ожидаемых” вундеркиндов, а остальные дети составляли группу контрольную. Ожидания учителей являли собой экспериментальную переменную, а интеллектуальное развитие детей - зависимую переменную. Через год тест был повторен и обнаружились значимые различия: развитие детей экспериментальной группы было выше, чем в контрольной. Несмотря на внешнюю убедительность, эксперимент не доказывает, что нтеллектуальное развитие детей обусловлено именно “эффектом Пигмалиона”. Вполне возможны и альтернативные объяснения. Имея дело с людьми, совершенно невозможно избежать реактивного эффекта, когда изучаемый признак неотделим от процедуры замера. Таблица 6.1. Схема экспериментального проекта
Социологические исследования, в которых независимая и зависимая переменные выделяются путем группировки данных, нельзя назвать экспериментом в полном смысле слова. Однако анализ результатов поддается методам, применяемым при управляемом экспериментальном воздействии. Обычно результатом неуправляемых социологических экспериментов с естественной возникающей независимой переменной является мера корреляции между признаками. При достаточно высокой корреляции гипотеза о неслучайном характере связи не отвергается. Низкая корреляция также не является решающим аргументом в пользу отсутствия причинной зависимости. Лучше всего использовать анализ корреляций для поиска тесных зависимостей, а уже потом выбирать из них гипотезы, требующие дополнительной валидизации.
|
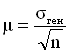где п - объем выборки.
.
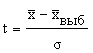не имеет. Вместе с тем, при достаточно большом числе наблюдений среднее квадратическое отклонение выборочных средних от общей средней становится равным среднему квадратическому отклонению генеральной совокупности, т. е. меру вариации в генеральной совокупности можно заменить мерой вариации в совокупности выборочной. В данном случае мю обозначает пределы, в которых может находиться с определенной вероятностью генеральная средняя: 
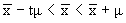
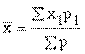денег у ребенка составляло тогда 45 руб. Затем надо выяснить, насколько велика разнородность обследованных по интересующей нас переменной, т. е. среднее квадратическое отклонение 
По формуле средней ошибки выборки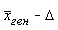 
=45-3,9=41,1 руб, верхний предел 
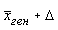=45+3,9=48,9 руб.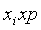
.
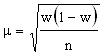где w - доля данного признака. Тогда 
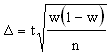Производим преобразование формулы и получаем. 
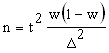Как и в случае с непрерывной переменной, остается неизвестной вариация генеральной совокупности. Выход из ситуации - максимизировать w(l - w). Максимальная вариация доли бывает при w = 0,5 и соответственно 1 - w = 0,5. Тогда w (1 - w) = 0,25. Это значение и подставляется в формулу.
- 5 %).
