Физические основы.
Известно, что свет можно рассматривать и как поток частиц (фотонов), распространяющихся по прямолинейным траекториям, и как электромагнитную волну, распространяющуюся в пространстве. При этом интенсивность света определяется амплитудой волны, а его цвет - частотой или длиной волны l. Сам процесс распространения света описывается уравнениями Максвелла. Произвольный луч света можно рассматривать как сумму волн с различными длинами, распространяющихся в одном направлении. Вклад волны с длиной l определяется функцией I(l), называемой спектральной кривой (спектральной характеристикой, спектральной функцией) данного луча света. В действительности один и тот же воспринимаемый глазом цвет может вызываться бесконечным количеством различных источников света с различными спектральными кривыми I(l). Поэтому при исследовании обычно ограничиваются конечным набором значений l, например для чистых красного (Red), зелёного (Green) и синего (Blue) цветов, и представляют все цвета в виде линейной комбинации этих базовых цветов. Именно таким образом организовано представление цветов и в телевизоре, и в дисплее. При таком подходе вместо спектральной функции мы получаем трёхмерный вектор (I(lRed), I(lGreen), I(lBlue)). Далее будем рассматривать распространение монохромной волны с длиной l. Процесс распространения света распадается на две части - распространение света в однородной среде и взаимодействие света с границей раздела двух сред. Когда волна (луч света) попадает на границу раздела двух сред, происходят его отражение и преломление. Распространение света в однородной среде. Распространение света в однородной среде происходит вдоль прямолинейной траектории с постоянной скоростью. Отношение скорости распространения света в вакууме к этой скорости называется коэффициентом преломления (индексом рефракции) среды:
Обычно этот коэффициент зависит от длины волны l. При распространении света в поглощающей среде имеет место экспоненциальное затухание по закону Бугера - Ламберта:
где I0 - освещённость при нулевой толщине среды, b - коэффициент затухания (коэффициент поглощения среды), l - расстояние, пройденной лучом в среде. 2. Определение вектора отражения. Рассмотрим случай зеркального (идеального) отражения.
Зеркальное отражение и идеальное преломление Будем считать все векторы единичными. Тогда из первого условия следует, что вектор r равен линейной комбинации векторов v и n, то есть r = a v + b n. Так как q v = qr, то (- v, n) = cos q v = cos qr = (r, n). Отсюда легко получается r = v - 2(v, n) n. (2.3) Несложно убедиться, что вектор, задаваемый соотношением (2.13), является единичным: r 2 = (v - 2(v, n) n)2 = v 2 - 2×2(v, n)(v, n) + 4(v, n)2 n 2 = 1 Определение вектора преломления. Рассмотрим случай идеального преломления. Луч, падающий в точку P в направлении вектора v, преломляется внутрь второй среды в направлении вектора p). Преломление подчиняется закону Синелиуса, согласно которому векторы v, n и p лежат в одной плоскости и для углов справедливо соотношение. h v sin q v = hp sin qp. (2.4) Найдём для вектора p явное выражение. Этот вектор можно представить в следующем виде: p = a v + b n. Соотношение (2.13) можно переписать так: sin q p = h sin q v, (2.5) где Тогда h2 sin2q v = sin2q p или h2(1 - cos2q v) = 1 - cos2q p. (2.7)
Так как cos q v = (- v, n), cos q p = (- p, n), то a2(v, n)2 + 2ab(v, n) + b2 = 1 + h2((v, n)2 - 1). (2.8) Из условия нормировки вектора p имеем || p ||2 = (p, p) = a2 + 2ab(v, n) + b2 = 1. (2.9) Вычитая это соотношение из равенства (2.8), имеем: a2((v, n)2 - 1) = h2((v, n)2 - 1), (2.10) откуда a = ±h. Из физических соображений следует, что a = h. b2 + 2bh(v, n) + h2 - 1 = 0, (2.11)
D = 4{1 + h2((v, n)2 - 1)}. (2.12) дискриминант которого равен Решение этого уравнения задаётся формулой
и, значит, вектор
где C = cos q v = -(v, n). (2.15) При этом случай, когда выражение под корнем отрицательно ({1+h2(С2 - 1)} < 0) соответствует так называемому полному внутреннему отражению, когда вся световая энергия отражается от границы раздела сред и преломления фактически не происходит.
|

 (2.1)
(2.1)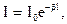 (2.2)
(2.2) Луч падает в точку Q в направлении v и отражается в направлении, задаваемом вектором r, определяемым следующим законом: вектор r лежит в той же плоскости, что и вектор v и вектор нормали к поверхности в точке падения n, а угол падения q v равен углу отражения qr
Луч падает в точку Q в направлении v и отражается в направлении, задаваемом вектором r, определяемым следующим законом: вектор r лежит в той же плоскости, что и вектор v и вектор нормали к поверхности в точке падения n, а угол падения q v равен углу отражения qr (2.6)
(2.6) Второй параметр (b) определяется из уравнения
Второй параметр (b) определяется из уравнения (2.13)
(2.13) (2.14)
(2.14)


