| Газ
| Молярная масса
 , кг/моль , кг/моль
| Эффективный диаметр молекулы
 , нм , нм
|
| Азот
| 0,028
| 0,37
|
| Водород
| 0,002
| 0,23
|
| Гелий
| 0,004
| 0,19
|
| Кислород
| 0,032
| 0,29
|
| Углекислый газ
| 0,044
| 0,40
|
| Воздух
| 0,029
| 0,35
|
ЛИТЕРАТУРА
1. Трофимова Т.И. Курс физики: Учебное пособие для вузов. ¾ М.: Высш. шк., 2001 — 542 с.: ил.
2. Детлаф А.А., Яворский Б.М. Курс физики: Учебное пособие для вузов. — М.: Высш. шк., 2001 ¾ 542 с.: ил.
Учебно-методическое издание
Составители:
Владимир Викторович ШЕГАЙ
Наталья Викторовна Дорохова
Владимир Петрович САФРОНОВ
УСТОЙЧИВОСТИ ДВИЖЕНИЯ
И КАЧЕСТВЕННОЙ ТЕОРИИ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Томск
Содержание
1. Второй метод Ляпунова для установившихся
движений............................................................................ 2
2. Критерии устойчивости по первому приближению
для установившихся движений...................................... 10
3. Влияние структуры сил на устойчивость движения.... 17
4. Устойчивость периодических движений……………….20
5. Приложение....................................................................... 20
Второй метод Ляпунова
для установившихся движений
Рассмотрим произвольную динамическую систему и допустим, что ее движение может быть описано системой ДУ, которая может быть приведена к нормальному виду:

 (1)
(1)
Здесь  - некоторые параметры, связанные с движением, как, например, координаты, скорости или вообще некоторые функции этих величин. Рассмотрим какое-нибудь частное движение нашей системы, которому соответствует некоторое частное решение
- некоторые параметры, связанные с движением, как, например, координаты, скорости или вообще некоторые функции этих величин. Рассмотрим какое-нибудь частное движение нашей системы, которому соответствует некоторое частное решение  уравнений (1). Мы будем это движение называть невозмущенным в отличие от других движений нашей системы, которые мы будем называть возмущенными. Разности значений величин
уравнений (1). Мы будем это движение называть невозмущенным в отличие от других движений нашей системы, которые мы будем называть возмущенными. Разности значений величин  в каком-нибудь возмущенном и невозмущенном движениях будем называть возмущениями, т.е.
в каком-нибудь возмущенном и невозмущенном движениях будем называть возмущениями, т.е.
 - возмущения
- возмущения 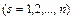
Для исследования устойчивости движения целесообразно преобразовать уравнения (1) к новым переменным  . Получим уравнения
. Получим уравнения
 ,
,
которые называются дифференциальными уравнениями возмущенного движения. Функции  представляют собой степенные ряды, расположенные по степеням
представляют собой степенные ряды, расположенные по степеням 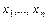 , сходящиеся в области
, сходящиеся в области  (
( - некоторая постоянная).
- некоторая постоянная).
О п р е д е л е н и е 1. Невозмущенное движение называется устойчивым по отношению к величинам  , если для всякого положительного числа
, если для всякого положительного числа  , как бы мало оно ни было, найдется другое положительное число
, как бы мало оно ни было, найдется другое положительное число  , такое, что для всех возмущенных движений
, такое, что для всех возмущенных движений  , для которых в начальный момент времени
, для которых в начальный момент времени  выполняются неравенства
выполняются неравенства
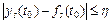 , (2)
, (2)
будут при всех  выполняться неравенства
выполняться неравенства
 . (3)
. (3)
Введем в рассмотрение функцию  , которая в некоторой окрестности начала координат
, которая в некоторой окрестности начала координат  обладает следующими свойствами:
обладает следующими свойствами:
1)  - однозначная функция;
- однозначная функция;
2) частные производные  непрерывны;
непрерывны;
3)  .
.
О п р е д е л е н и е 2. Если в окрестности начала координат (при  , где
, где  - достаточно малое положительное число) функция
- достаточно малое положительное число) функция 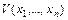 кроме нуля может принимать значения только одного знака, то она называется знакопостоянной ( положительной или отрицательной).
кроме нуля может принимать значения только одного знака, то она называется знакопостоянной ( положительной или отрицательной).
О п р е д е л е н и е 3. Если знакопостояннаяфункция обращается в нуль только при  , то она называется знакоопределенной ( положительной или отрицательной).
, то она называется знакоопределенной ( положительной или отрицательной).
О п р е д е л е н и е 4. Функция  называется знакопеременной, если она не является ни знакоопределенной, ни знакопостоянной и, следовательно, может принимать как положительные, так и отрицательные значения.
называется знакопеременной, если она не является ни знакоопределенной, ни знакопостоянной и, следовательно, может принимать как положительные, так и отрицательные значения.
Т е о р е м а 1 (первая теорема Ляпунова об устойчивости). Если для ДУ возмущенного движения возможно найти знакоопределенную функцию  , полная производная которой по времени, составленная в силу этих уравнений, есть функция знакопостоянная, знака, противоположного с
, полная производная которой по времени, составленная в силу этих уравнений, есть функция знакопостоянная, знака, противоположного с 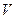 , или тождественно обращается в нуль, то невозмущенное движение устойчиво.
, или тождественно обращается в нуль, то невозмущенное движение устойчиво.
Т е о р е м а 2 (вторая теорема Ляпунова об устойчивости). Если для ДУ возмущенного движения возможно найти знакоопределенную функцию  , полная производная которой по времени, составленная в силу этих уравнений, есть функция также знакоопределенная, знака, противоположного с
, полная производная которой по времени, составленная в силу этих уравнений, есть функция также знакоопределенная, знака, противоположного с  , или тождественно обращается в нуль, то невозмущенное движение устойчиво асимптотически.
, или тождественно обращается в нуль, то невозмущенное движение устойчиво асимптотически.
Т е о р е м а 3 (первая теорема Ляпунова о неустойчивости). Если для ДУ возмущенного движения возможно найти функцию 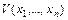 , такую, что ее полная производная по времени
, такую, что ее полная производная по времени  , составленная в силу этих уравнений, есть функция знакоопределенная, а сама функция
, составленная в силу этих уравнений, есть функция знакоопределенная, а сама функция  не будет знакопостоянной, знака, противоположного с
не будет знакопостоянной, знака, противоположного с  , то невозмущенное движение неустойчиво.
, то невозмущенное движение неустойчиво.
Т е о р е м а 4 (вторая теорема Ляпунова о неустойчивости). Если существует функция  такая, что ее полная производная по
такая, что ее полная производная по  в силу уравнений возмущенного движения имеет в области
в силу уравнений возмущенного движения имеет в области 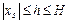 вид
вид
 ,
,
где  - положительная постоянная, а
- положительная постоянная, а  или тождественно обращается в нуль или представляет собой знакопостоянную функцию, и если в последнем случае функция
или тождественно обращается в нуль или представляет собой знакопостоянную функцию, и если в последнем случае функция  не является знакопостоянной, знака, противоположного с
не является знакопостоянной, знака, противоположного с  , то невозмущенное движение неустойчиво.
, то невозмущенное движение неустойчиво.
Т е о р е м а 5 (теорема Четаева Н.Г.). Если для ДУ возмущенного движения можно найти такую функцию 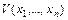 , что 1) в сколь угодно малой окрестности начала координат существует область, где
, что 1) в сколь угодно малой окрестности начала координат существует область, где  , и 2) во всех точках области
, и 2) во всех точках области  производная
производная  принимает положительные значения, то невозмущенное движение неустойчиво.
принимает положительные значения, то невозмущенное движение неустойчиво.

 , кг/моль
, кг/моль
 , нм
, нм

 (1)
(1) - некоторые параметры, связанные с движением, как, например, координаты, скорости или вообще некоторые функции этих величин. Рассмотрим какое-нибудь частное движение нашей системы, которому соответствует некоторое частное решение
- некоторые параметры, связанные с движением, как, например, координаты, скорости или вообще некоторые функции этих величин. Рассмотрим какое-нибудь частное движение нашей системы, которому соответствует некоторое частное решение  уравнений (1). Мы будем это движение называть невозмущенным в отличие от других движений нашей системы, которые мы будем называть возмущенными. Разности значений величин
уравнений (1). Мы будем это движение называть невозмущенным в отличие от других движений нашей системы, которые мы будем называть возмущенными. Разности значений величин  - возмущения
- возмущения 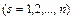
 . Получим уравнения
. Получим уравнения ,
, представляют собой степенные ряды, расположенные по степеням
представляют собой степенные ряды, расположенные по степеням 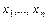 , сходящиеся в области
, сходящиеся в области  (
( - некоторая постоянная).
- некоторая постоянная). , как бы мало оно ни было, найдется другое положительное число
, как бы мало оно ни было, найдется другое положительное число  , такое, что для всех возмущенных движений
, такое, что для всех возмущенных движений  , для которых в начальный момент времени
, для которых в начальный момент времени  выполняются неравенства
выполняются неравенства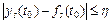 , (2)
, (2) выполняться неравенства
выполняться неравенства . (3)
. (3) , которая в некоторой окрестности начала координат
, которая в некоторой окрестности начала координат  обладает следующими свойствами:
обладает следующими свойствами: - однозначная функция;
- однозначная функция; непрерывны;
непрерывны; .
. - достаточно малое положительное число) функция
- достаточно малое положительное число) функция 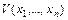 кроме нуля может принимать значения только одного знака, то она называется знакопостоянной ( положительной или отрицательной).
кроме нуля может принимать значения только одного знака, то она называется знакопостоянной ( положительной или отрицательной). , то она называется знакоопределенной ( положительной или отрицательной).
, то она называется знакоопределенной ( положительной или отрицательной).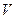 , или тождественно обращается в нуль, то невозмущенное движение устойчиво.
, или тождественно обращается в нуль, то невозмущенное движение устойчиво. , или тождественно обращается в нуль, то невозмущенное движение устойчиво асимптотически.
, или тождественно обращается в нуль, то невозмущенное движение устойчиво асимптотически. , составленная в силу этих уравнений, есть функция знакоопределенная, а сама функция
, составленная в силу этих уравнений, есть функция знакоопределенная, а сама функция  в силу уравнений возмущенного движения имеет в области
в силу уравнений возмущенного движения имеет в области 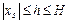 вид
вид ,
, - положительная постоянная, а
- положительная постоянная, а  или тождественно обращается в нуль или представляет собой знакопостоянную функцию, и если в последнем случае функция
или тождественно обращается в нуль или представляет собой знакопостоянную функцию, и если в последнем случае функция  , и 2) во всех точках области
, и 2) во всех точках области 


