Пусть исследование устойчивости движения системы относительно переменных  и
и 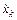 сводится к анализу дифференциальных уравнений возмущенного движения, которые можно представить в виде одного матричного уравнения
сводится к анализу дифференциальных уравнений возмущенного движения, которые можно представить в виде одного матричного уравнения
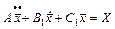 . (1)
. (1)
В этом уравнении 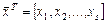 - вектор-столбец параметров движения;
- вектор-столбец параметров движения;  - заданные квадратные матрицы порядка
- заданные квадратные матрицы порядка 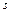 с постоянными элементами.
с постоянными элементами.
 - вектор – столбец элементов, являющихся функциями параметров движения
- вектор – столбец элементов, являющихся функциями параметров движения 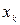 и их производных
и их производных 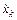 в степенях
в степенях
не ниже второй и обращающимися в нуль, если все  и
и 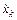 обращаются в нуль. Предполагается, что матрица
обращаются в нуль. Предполагается, что матрица  симметрична (
симметрична (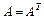 ) и ее квадратичная форма
) и ее квадратичная форма
 (2)
(2)
определенно-положительная.
В дальнейшем будем считать, что уравнение (1) описывает некоторую механическую систему, в которой переменные 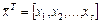 являются координатами, их производные по времени
являются координатами, их производные по времени 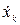 - составляющими скоростей, квадратичная форма (2) – ее кинетической энергией, а составляющие
- составляющими скоростей, квадратичная форма (2) – ее кинетической энергией, а составляющие 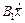 и
и 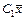 - силами, приложенными к системе.
- силами, приложенными к системе.
Представим матрицы 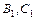 в виде симметричных и кососимметричных матриц, положив
в виде симметричных и кососимметричных матриц, положив
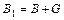
 (3)
(3)
где  - симметричные матрицы, а
- симметричные матрицы, а 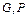 - кососимметричные матрицы, равные
- кососимметричные матрицы, равные
 (4)
(4)
Подставим полученные выражения в уравнение (1). Оно примет вид:
 . (5)
. (5)
Определим составляющие полученного уравнения.
1. Силы 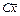 с симметричной матрицей
с симметричной матрицей  называются потенциальными(или консервативными) силами, а квадратичная форма
называются потенциальными(или консервативными) силами, а квадратичная форма
 (6)
(6)
потенциальной энергией системы. Если потенциальная энергия П имеет минимум, то все ее коэффициенты положительны, а при максимуме П – отрицательны. Практически силы 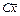 - это линейные части естественных потенциальных сил тяжести, упругости и т. п. Нелинейные части этих сил могут входить составляющими правых частей системы уравнений.
- это линейные части естественных потенциальных сил тяжести, упругости и т. п. Нелинейные части этих сил могут входить составляющими правых частей системы уравнений.
2. Силы  с симметричной матрицей
с симметричной матрицей  называются диссипативными силами, а квадратичная форма
называются диссипативными силами, а квадратичная форма
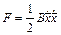 ,
,
будучи неотрицательной называется функцией рассеивания или диссипативной функцией Релея. Если 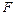 - определенно – положительнаяквадратичная форма, то диссипация называется полной, в противном случае – неполной.
- определенно – положительнаяквадратичная форма, то диссипация называется полной, в противном случае – неполной.
3. Силы  , линейно зависящие от составляющих скоростей, с кососимметричной матрицей коэффициентов
, линейно зависящие от составляющих скоростей, с кососимметричной матрицей коэффициентов 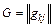 называется гироскопическими силами.
называется гироскопическими силами.
4. Силы 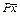 , линейно зависящие от координат
, линейно зависящие от координат 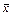 , с кососимметричной матрицей коэффициентов
, с кососимметричной матрицей коэффициентов 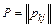 называются циркуляционными или неконсервативными.
называются циркуляционными или неконсервативными.
5. Силы 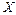 называются нелийными. Элементы матрицы
называются нелийными. Элементы матрицы 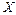 содержат координаты
содержат координаты  составляющие скорости
составляющие скорости 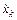 в степени не ниже второй и обращаются в нуль если последние все обращаются в нуль. Таким образом, учитываемые в рассматриваемом случае уравнения учитывают только небольшой класс нелинейных сил.
в степени не ниже второй и обращаются в нуль если последние все обращаются в нуль. Таким образом, учитываемые в рассматриваемом случае уравнения учитывают только небольшой класс нелинейных сил.
Вопросы и задачи:
1. Уравнения движения в декартовых координатах имеет вид
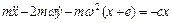 ,
,
 .
.
Показать, что они содержат гироскопические силы. Определить степень неустойчивости в отсутствии гироскопических сил.
2. Исследовать устойчивость движения электрона в постоянном магнитном поле, если уравнение движения электрона имеет вид
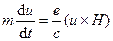 ,
,
где  - масса электрона; u – вектор скорости электрона; е – заряд электрона; с – электродинамическая постоянная, равная скорости света (с =3·1010 см/с); Н – напряженность магнитного поля.
- масса электрона; u – вектор скорости электрона; е – заряд электрона; с – электродинамическая постоянная, равная скорости света (с =3·1010 см/с); Н – напряженность магнитного поля.

 и
и 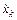 сводится к анализу дифференциальных уравнений возмущенного движения, которые можно представить в виде одного матричного уравнения
сводится к анализу дифференциальных уравнений возмущенного движения, которые можно представить в виде одного матричного уравнения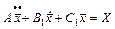 . (1)
. (1)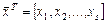 - вектор-столбец параметров движения;
- вектор-столбец параметров движения;  - заданные квадратные матрицы порядка
- заданные квадратные матрицы порядка 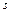 с постоянными элементами.
с постоянными элементами. - вектор – столбец элементов, являющихся функциями параметров движения
- вектор – столбец элементов, являющихся функциями параметров движения 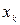 и их производных
и их производных  симметрична (
симметрична (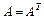 ) и ее квадратичная форма
) и ее квадратичная форма (2)
(2)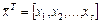 являются координатами, их производные по времени
являются координатами, их производные по времени 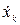 - составляющими скоростей, квадратичная форма (2) – ее кинетической энергией, а составляющие
- составляющими скоростей, квадратичная форма (2) – ее кинетической энергией, а составляющие 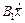 и
и 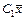 - силами, приложенными к системе.
- силами, приложенными к системе.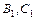 в виде симметричных и кососимметричных матриц, положив
в виде симметричных и кососимметричных матриц, положив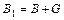
 (3)
(3) - симметричные матрицы, а
- симметричные матрицы, а 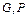 - кососимметричные матрицы, равные
- кососимметричные матрицы, равные (4)
(4) . (5)
. (5)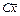 с симметричной матрицей
с симметричной матрицей  называются потенциальными(или консервативными) силами, а квадратичная форма
называются потенциальными(или консервативными) силами, а квадратичная форма (6)
(6) с симметричной матрицей
с симметричной матрицей  называются диссипативными силами, а квадратичная форма
называются диссипативными силами, а квадратичная форма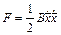 ,
,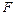 - определенно – положительнаяквадратичная форма, то диссипация называется полной, в противном случае – неполной.
- определенно – положительнаяквадратичная форма, то диссипация называется полной, в противном случае – неполной. , линейно зависящие от составляющих скоростей, с кососимметричной матрицей коэффициентов
, линейно зависящие от составляющих скоростей, с кососимметричной матрицей коэффициентов 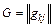 называется гироскопическими силами.
называется гироскопическими силами.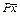 , линейно зависящие от координат
, линейно зависящие от координат 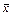 , с кососимметричной матрицей коэффициентов
, с кососимметричной матрицей коэффициентов 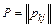 называются циркуляционными или неконсервативными.
называются циркуляционными или неконсервативными.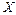 называются нелийными. Элементы матрицы
называются нелийными. Элементы матрицы 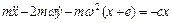 ,
, .
.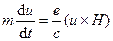 ,
, - масса электрона; u – вектор скорости электрона; е – заряд электрона; с – электродинамическая постоянная, равная скорости света (с =3·1010 см/с); Н – напряженность магнитного поля.
- масса электрона; u – вектор скорости электрона; е – заряд электрона; с – электродинамическая постоянная, равная скорости света (с =3·1010 см/с); Н – напряженность магнитного поля.


