Критерии устойчивости по первому приближению для установившихся движений
Пусть автономная динамическая система описывается следующей системой дифференциальных уравнений:
Точка
является одним из состояний равновесия этой динамической системы. Будем полагать, что состояние равновесия изолированное, то есть имеется окрестность состояния равновесия P 0, в которой нет других состояний равновесия. Линеаризуем систему (1) в окрестности состояния равновесия P 0:
Сделав замену
Характеристическое уравнение системы (4) запишем в виде:
где D (
Теорема 1. Если все корни характеристического уравнения (5) линеаризованной системы (4) имеют действительные части меньшие нуля, то состояние равновесия (2) системы (1) асимптотически устойчиво, каковы бы ни были нелинейные члены. Теорема 2. Если среди корнейхарактеристического уравнения (5) линеаризованной системы (4) имеется хотя бы один корень с действительной частью большей нуля, то состояние равновесия (2) неустойчиво при любых нелинейных членах. Теорема 3. Если характеристическое уравнение (5) линеаризованной системы (4) не имеет корней с действительной частью большей нуля, но имеет корни с вещественной частью равной нулю, то а) невозмущенное движение будет устойчиво (не асимптотически), если корни с нулевой вещественной частью соответствуют простым элементарным делителям; б) невозмущенное движение будет неустойчивым, если хотя бы один корень с нулевой вещественной частью является кратным корнем соответствующего элементарного делителя. Критерий Гурвица. Развернем характеристическое уравнение (5) по степеням
где ai Критерий Гурвица дает возможность, не вычисляя корней характеристического уравнения (6), судить о знаках реальных частей его корней только с помощью исследования коэффициентов этого многочлена и, в конечном итоге, судить об устойчивости состояния равновесия. Введем обозначения:
Формулировка критерия Гурвица. Для того чтобы все корни уравнения (6) при действительных значениях a 0> 0 и ak имели реальную часть меньше нуля, необходимо и достаточно, чтобы удовлетворялись неравенства:
Построим матрицу Гурвица для уравнения (6):
Частные случаи критерия Гурвица: n = 2: n = 3: n = 4:
Замечание 1. Если хотя бы одно из неравенств (7) имеет противоположный смысл, то среди корней уравнения (6) имеются корни с положительной действительной частью. Замечание 2. Необходимым условием отрицательности действительных частей всех корней уравнения (6) является положительность Замечание 3. Если при a 0> 0 хотя бы один из коэффициентов ak отрицателен, то среди корней уравнения (6) имеются корни с положительной действительной частью.
Вопросы и задачи: 1. Исследовать устойчивость нулевого решения системы
2. Корни характеристических уравнений таковы:
а)
б)
в) Какие заключения можно сделать об устойчивости по первому приближению соответствующих состояний равновесия?
3. С помощью теорем Ляпунова об устойчивости по первому приближению исследовать на устойчивость нулевое состояние равновесия. а) б) в)
д)
4. Найти значения параметров a и b, при которых асимптотически устойчиво нулевое решение следующих систем.
а) б) в) г) д)
5. Линеаризовав систему дифференциальных уравнений, решить вопрос об устойчивости нулевого состояния равновесия.
а)
б)
в) г) д) е)
з)
к) 6. По характеристическому уравнению D(
ж)
к)
м)
о)
р) с) т) у) ф) х) ц) ч)
7. Исследовать, при каких значениях параметров a и b нулевое решение асимптотически устойчиво.
а) б) в) г) д) е) ж) з)
8. Дано уравнение
9. Движение автоматической системы регулирования описывается следующими ДУ
где
10. Двухроторный гирокомпас Аншютца[1] с гидравлическим успокоителем широко используется в некоторых странах. Если гироскоп такого типа установлен на корабле, северная составляющая путевой скорости которого постоянна, то дифференциальные уравнения движения гироскопа имеют вид:
Здесь Определить условие асимптотической устойчивости.
11. Гирогоризонткомпас – устройство, которое иногда используется на движущемся корабле для одновременного определения географического меридиана и горизонтальной плоскости. На неподвижном относительно Земли основании дифференциальные уравнения возмущенного движения гирогоризонткомпаса могут быть сведены к двум совершенно аналогичным системам уравнений. Первая система имеет вид:
Здесь Во второй аналогичной системе уравнений возмущенного движения Найти условие асимптотической устойчивости движения гирогоризонткомпаса. 12. Обозначим моменты инерции твердого тела относительно осей
|

 (1)
(1) , координаты которой удовлетворяют системе уравнений
, координаты которой удовлетворяют системе уравнений (2)
(2) (3)
(3) , обозначив
, обозначив  и пренебрегая нелинейными членами
и пренебрегая нелинейными членами 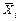 ,получим линеаризованную систему
,получим линеаризованную систему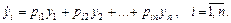 (4)
(4) (5)
(5) ) – характеристический многочлен, определяемый равенством
) – характеристический многочлен, определяемый равенством
 (6)
(6) R и зависят от параметров системы, a 0> 0.
R и зависят от параметров системы, a 0> 0.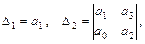
 .
. (7)
(7)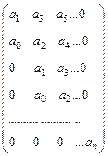


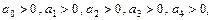

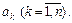





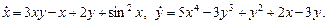
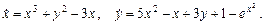


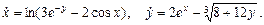
 е)
е) 

 ж)
ж) 



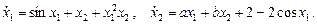

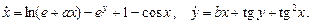




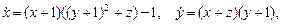



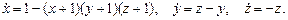





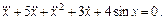































 Выделите область устойчивости состояния равновесия в плоскости параметров A и B.
Выделите область устойчивости состояния равновесия в плоскости параметров A и B.
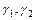 и
и  - координаты системы;
- координаты системы; 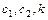 и
и  - положительные параметры системы. Определить какому условию должны отвечать параметры системы, чтобы движение было асимптотически устойчиво.
- положительные параметры системы. Определить какому условию должны отвечать параметры системы, чтобы движение было асимптотически устойчиво. ,
, ,
, .
. и
и  - вариации (отклонения) координат компаса от их значений при динамическом равновесии;
- вариации (отклонения) координат компаса от их значений при динамическом равновесии;  - частота собственных колебаний чувствительного элемента (гиросферы);
- частота собственных колебаний чувствительного элемента (гиросферы);  - угловая скорость вращения Земли;
- угловая скорость вращения Земли;  - широта, на которой находится корабль;
- широта, на которой находится корабль; 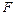 - коэффициент трения жидкости в гидравлическом успокоителе,
- коэффициент трения жидкости в гидравлическом успокоителе,  ;
;  и
и  - маятниковые моменты жидкого успокоителя и гиросферы соответственно;
- маятниковые моменты жидкого успокоителя и гиросферы соответственно;  - члены высших порядков по
- члены высших порядков по  .
. ,
, .
. - величина, пропорциональная углу отклонения от плоскости меридиана;
- величина, пропорциональная углу отклонения от плоскости меридиана;  - вариация конструктивного угла;
- вариация конструктивного угла;  и
и  - коэффициенты, характеризующие диссипативные силы;
- коэффициенты, характеризующие диссипативные силы; 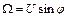 ;
;  - члены высших порядков по
- члены высших порядков по  .
. определяют угол отклонения от горизонтальной плоскости и вариацию другого конструктивного угла.
определяют угол отклонения от горизонтальной плоскости и вариацию другого конструктивного угла. через
через 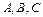 соответственно таким образом, что либо
соответственно таким образом, что либо 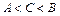 , либо
, либо  . Доказать, что перманентное вращение твердого тела относительно оси
. Доказать, что перманентное вращение твердого тела относительно оси  неустойчиво.
неустойчиво.


