Устойчивость равновесия потенциальных систем
Для наиболее распространенного класса потенциальных механических систем исследование устойчивости их состояния равновесия основывается на теореме Лагранжа-Дирихле: равновесное состояние потенциальной системы устойчиво в том случае. Если в этом состоянии ее потенциальная энергия
Вопросы и задачи: 1. Определить тип функции Ляпунова а) б)
2. Исследовать устойчивость нулевого решения системы а)
б)
в)
г)
д)
е)
3. Даны функции, производные которых по времени в силу уравнений возмущенного движения соответственно равны: 1.
2. 3. 4. Можно ли воспользоваться этими функциями для определения характера устойчивости движения?
4. Являются ли приведенные ниже функции знакоопределенными? Знакопостоянными? Если Да, то в какой области? а) б) в) г) д) е) ж)
5. Дайте развернутое определение неустойчивости состояния равновесия.
6. В следующих задачах исследуйте устойчивость нулевого решения. Исследуйте асимптотическую устойчивость нулевого состояния равновесия. а)
б)
в)
г)
д)
е)
ж)
з)
7. Исследовать устойчивость нулевого состояния равновесия систем: а)
б)
в) г)
д)
е)
ж)
з)
и)
к)
л)
м) 8. По равномерно вращающемуся вокруг вертикальной оси кольца радиуса
Рисунок 1 Определить положение динамического равновесия колечка, составить уравнение возмущенного движения относительно равновесного положения и выделить уравнение первого приближения.
9. Двойной маятник, изображенный на рис. 2, удерживается в верхнем вертикальном положении двумя спиральными пружинами жесткости
Рисунок 2
Составить уравнение первого приближения возмущенного движения относительно верхнего вертикального положения. Массой стержней и силами сопротивления пренебречь. 10. Исследовать устойчивость вертикального положения равновесия системы обращенных маятников, изображенной на рис. 3, где показаны все размеры системы. Массы всех маятников и жесткости пружин одинаковы и равны
Рисунок 3
|

 имеет изолированный минимум. При этом характер этого минимума может быть как гладким (когда в точке минимума функция
имеет изолированный минимум. При этом характер этого минимума может быть как гладким (когда в точке минимума функция  дифференцируема по всем обобщенным координатам
дифференцируема по всем обобщенным координатам  ), так и зубцовым (когда по некоторым координатам дифференцируемость отсутствует). В первом случае положения равновесия
), так и зубцовым (когда по некоторым координатам дифференцируемость отсутствует). В первом случае положения равновесия  определяются из соотношений
определяются из соотношений  , а их устойчивость зависит от свойств матрицы
, а их устойчивость зависит от свойств матрицы  в точке
в точке  . Признаком устойчивости является выполнение критерия Сильвестра для этой матрицы в точке
. Признаком устойчивости является выполнение критерия Сильвестра для этой матрицы в точке  ;
; .
.

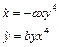
 ,
,  >0,
>0,  >0
>0
 ,
,  ,
,  ,
, 



 ,
,  ,
, 


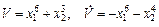

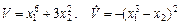



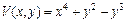










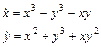

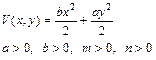





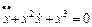



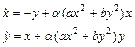











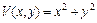


 может свободно без трения перемещаться колечко М (см. рисунок 1). Угловая скорость равномерного вращения кольца равна
может свободно без трения перемещаться колечко М (см. рисунок 1). Угловая скорость равномерного вращения кольца равна  .
.
 и
и 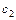 . Точечные массы маятников равны
. Точечные массы маятников равны  и
и  , а длины невесомых стержней -
, а длины невесомых стержней -  и
и  , соответственно. В верхнем вертикальном положении маятников спиральные пружины не деформированы.
, соответственно. В верхнем вертикальном положении маятников спиральные пружины не деформированы.
 и
и  , соответственно. Полагаем, что массой стрежней можно пренебречь, а массы
, соответственно. Полагаем, что массой стрежней можно пренебречь, а массы 



