Предлагаем фрагмент урока по теме«Час. Минута»учителя Г.М. Рябихиной (школа № 10 г. Таганрога).

Цель урока: 1) познакомить учащихся с понятиями час и минута как с единицами измерения времени; 2) закрепить умение находить долю числа и число по его доле; 3) продолжить развитие познавательного интереса к предмету.

Оборудование: табель-календарь, таблица отношений единиц измерения времени, циферблат с подвижными стрелками, таблица с изображениями различныx часов (от песочных до электронных), секундомер 1. Подготовительная работа к изучению нового материала построена на основе ответов на вопросы:

– Назовите известные вам единицы времени, начиная с самой крупной. (Год, месяц, неделя, сутки).

– Сколько месяцев в году? Назовите их по порядку.

Какой месяц в году самый короткий? Сколько в нем суток? Сколько полных недель?

– Как вы думаете, есть ли единицы измерения времени, меньшие, чем сутки? (Это час, минута.)

2. На этом уроке мы больше узнаем об этих единицах измерения времени, узнаем соотношение между ними.

Учитель демонстрирует модель циферблата с подвижными стрелками и рассказывает об устройстве часов, обращаясь постоянно с вопросами к учащимся:

– Как называют большую стрелку часов? маленькую?

По кругу циферблата на одинаковом расстоянии друг от друга расположены числа от 1 до 12. Между ними короткие черточки.

– Сосчитайте, сколько расстояний между черточками, например от 1 до 2. Одно такое расстояние большая стрелка проходит за 1 минуту. Вы не забыли, сколько времени движется часовая стрелка от одной большой черточки до другой? (1 час.)

Так учащиеся повторили материал, известный им еще из I класса, и перешли к работе с учебником. Выполнив задания из учебника, учащиеся делают запись в тетради:

1 сут. = 24 ч 1 ч = 60 мин

С целью закрепления знаний о соотношении между сутками и часом, часом и минутой учащиеся отвечают на вопросы: сколько часов составляет половина суток? Четверть суток? Сколько часов в двух сутках? В трех сутках? Сколько минут в половине часа? В одной четверти часа? В одной трети часа? Сколько всего минут в 1 ч 15 мин; в 2 ч; в 2 ч 30 мин?

3. Продолжая работу, учитель сообщает:

– У меня в руках секундомер (показывает его). Чтобы вы получили конкретное представление о длительности одной минуты, вы по моему сигналу должны начать и закончить писать двузначные числа в порядке возрастания, начиная с любого числа.

По истечении минуты учитель выясняет, кто и сколько успел записать двузначных чисел. Затем предлагает решить примеры и записать в тетради только ответы (примеры записаны на доске) за это же время:

4 × 3	8 × 4	42: 6	49: 7
6 × 5	9 × 5	24: 3	9 × 8
9 × 7	6: 2	64: 8	14: 2
6 × 8	12: 4	7 × 9	7 × 8
2 × 9	36: 9	81: 9	54: 6

 

После этого учитель просит посчитать числа, начиная от 21, проговаривая шепотом числительные – двадцать один, двадцать два и т.д., и делает обобщение: «За 1 минуту можно прочитать 60–70 слов, назвать числа от 21 до 81, решить 15–20 примеров, связанных со знанием табличных случаев умножения и деления и записать результаты». Вывод: минута – это совсем не маленькая единица времени, если ее использовать разумно.

4. Приступая к определению времени по числам с точностью до минуты, учитель выясняет:

– Как должны быть расположены стрелки на часах, если они показывают 9 часов? (Часовая стрелка показывает на цифру 9, а минутная – на цифру 12.)

– Как будут располагаться стрелки часов через 1 час? (Часовая стрелка будет показывать 10, а минутная – 12.)

Эти задания выполняются с использованием демонстрационного и индивидуальных циферблатов.

Далее вывешивается плакат, на котором часы показывают разное время. Дается задание определить время по часам. Учитель напоминает, чтобы дети не забывали при определении времени учитывать положение не только часовой, но и минутной стрелки. Минутная стрелка проходит расстояние от одной маленькой черточки до другой за 1 минуту (определяют это по секундомеру).

– Посчитайте, сколько минут пройдет, пока минутная стрелка перейдет от одной большой черточки до другой. (Пройдет 5 минут.)

– За сколько минут большая стрелка пройдет половину круга? (За 30 минут.)

– Четверть круга? (За 15 минут.)

– Сколько полных оборотов сделает минутная стрелка за 1 час? (1 оборот.)

Определяя время по часам, изображенным на рисунке, учитель требует от учащихся разной формы чтения; например: без четверти 6, пять часов 45 минут, 45 минут шестого, без 15 минут шесть, половина второго, четверть седьмого и т.д.

В заключение учащиеся на доске и в тетрадях выполняют задание:

1 год =... сут.

1 сут. =... ч

1 ч =... мин

5. Завершая урок, учитель проводит беседу из истории математики. Он вывешивает плакат, на котором изображены различные виды часов – от песочных, водяных, солнечных до электронных.

Часы не всегда имели такой привычный для нас вид, как в настоящее время.

Для того чтобы измерять небольшие промежутки времени, египетские ученые изобрели часы. Первые часы были солнечными (покалывает рисунок), они работали только днем. Вы видите на рисунке две сколоченные уголком планки? Это и есть египетские солнечные часы. А вот солнечные часы, которые стоят в г. Таганроге у спуска к набережной (показывает рисунок).

Утром, когда солнце только вставало, место тени на длинной планке отмечали зарубкой. Считалось, что час прошел, когда тень проходила от одной отметки до другой. В полдень часы переворачивали другим концом, и тень, увеличиваясь, опять шла по отметкам. Получалось шесть утренних часов и шесть вечерних.

Позднее египтяне изобрели водяные часы, которые могли показывать время и ночью. Они так и назывались «ночные часы».

Водяные часы – это сосуд, из которого черта дырочку постоянно вытекает вода (показывает на рисунке водяные часы). Дырочка таких размеров, что вся вода через нее вытекает ровно за час. Потом нужно снова наполнять сосуд водой. Это не очень удобный, но достаточно точный способ измерения времени. Видимо, отсюда и происходят выражения время истекло, время течет. А вот песочные часы (показывает рисунок). Их используют в медицине и до сих пор для определения промежутка времени, отведенного на ту или иную процедуру (в ванне, бассейне и т.п.).

В настоящее время существуют часы разных видов – от механических до электронных (показывает плакат с изображением различных часов, на которых отмечено разнос время).

В качестве закрепления пройденного материала учитель просит определить время на часах, изображенных на плакате.

1.6. МЕТОДИКА ИЗУЧЕНИЯ ЭЛЕМЕНТОВ ГЕОМЕТРИИ
В НАЧАЛЬНОМ КУРСЕ МАТЕМАТИКИ

План:

1. Задачи изучения геометрического материала.

2. Общие вопросы методики работы над геометрическим материалом.

3. Задачи геометрического содержания.

4. Формирование представлений и понятий о геометрических фигурах:

- существенные и несущественные признаки;

- содержание и объем понятия;

- классификация понятий.

5. Последовательность работы по подготовке и изучению периметра прямоугольника (квадрата):

- выяснение общих представлений младших школьников о прямоугольнике;

- знакомство с понятием «прямоугольник» на основе суждения понятия «многоугольник»;

- прямые и непрямые углы;

- изучение свойств прямоугольника, практическое их обоснование.

6. Возможные ошибки в рассуждениях учащихся при изучении геометрического материала.

 

Рекомендательная литература

1. Абдуллаева К. Пути устранения некоторых геометрических ошибок учащихся // Начальная школа. – 1978. – № 2. – С. 14-17.

2. Коган Т.Л. Формирование геометрических понятий // Начальная школа. – 1981. – № 2. – С. 26-28.

3. Крайнюк В.М. Практическая направленность в изучении геометрического материала // Начальная школа. – 1980. – № 1. – С. 4-36.

4. Колягин Ю.М., Тарасова О.В. Наглядная геометрия в начальных классах // Начальная школа. – 1996. – № 9. – С. 70-74.

5. Левенберг Л.Ш. Практическая направленность в изучении геометрического материала // Начальная школа. – 1982. – № 10. – С. 47-50.

6. Пазушко Ж.И. Развивающая геометрия в начальной школе // Начальная школа. – 1999. – №1. – С. 93-95.

7. Савенков А.И. Задачи для развития объемно-пространственного мышления школьников // Начальная школа. – 1998. – № 7. – С. 59-63.

8. Шмырева Г.Г. Практические работы при ознакомлении с геометрическими фигурами в 1-м классе // Начальная школа. – 1982. – № 10. – С. 54-57.

 

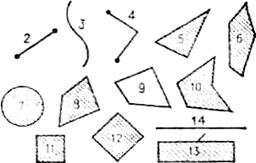
Основное содержание геометрического материала, включенного в программу и реализованного в системе тщательно отобранных задач, направлено на формирование достаточно полной системы геометрических представлений (включающей образы геометрических фигур, их элементов, отношений между фигурами, их элементами).

На этой основе формируются пространственные представления и воображение, развивается речь и мышление учащихся, организуется целенаправленная работа по формированию важных практических навыков. Важнейшей задачей учителя является определение методики, раскрывающей содержание геометрического материалана том уровне, который должен быть достигнут учащимися к моменту их перехода в IV класс, а также ведущих направлений изучения этого материала.

Для формирования геометрических представлений работа должна проводиться следующим образом: свойства фигур учащиеся выявляют экспериментально, одновременно усваивают необходимую терминологию и навыки; основное место в обучении должны занимать практические работы учеников, наблюдения и работы с геометрическими объектами.

Оперируя разнообразными предметами, моделями геометрических фигур, выполняя большое число наблюдений и опытов, учащиеся подмечают наиболее общие их признаки (не зависящие от материала, цвета, положения, массы и т.п.).

В методике формирования геометрических представлений важно идти от «вещи» к фигуре (к ее образу), а также наоборот – от образа фигуры к реальной вещи.

Это достигается систематическим использованием приема материализации геометрических образов. Например, прямая линия не только вычерчивается с помощью линейки, представление о ней дает и край – ребро линейки, натянутая нить, линия сгиба листа бумаги, линия пересечения двух плоскостей (например, плоскости стены и плоскости потолка). Отвлекаясь от конкретных свойств материальных вещей, учащиеся овладевают геометрическими представлениями. Так, например, можно видоизменять способ деления многоугольника отрезком на части. Вначале это может быть перегибание бумажного многоугольника. В этом случае отрезок (линия сгиба) реально делит многоугольник на 2 части. Этот опыт полезно продолжить, разрезав многоугольник по линии сгиба на 2 многоугольника. Несколько позже эту же задачу полезно решить на чертеже, вначале путем непосредственного проведения (вычерчивания) отрезка, затем прикладыванием указки.

В I классе в основном завершается первоначальное ознакомление с фигурами и их названиями. Это делается на основе рассмотрения окружающих вещей, готовых моделей и изображений фигур. У детей постепенно вырабатывается схема изучения фигур, схема их анализа и синтеза, облегчающая усвоение свойств каждой фигуры.

Значительное место в методике должно отводиться применению приема сопоставления и противопоставления геометрических фигур. В I классе это позволит из множества фигур наглядно (без помощи определений) выделять множество кругов, множество многоугольников, множество линий и т.д.; во II и III классах – уточнять свойства фигур, классифицировать их. Больше внимания следует уделять противопоставлению и сопоставлению плоских фигур (круг – многоугольник, окружность – круг и т.д.); плоских и пространственных фигур (квадрат – куб, круг –шар и пр.).

Причем эта работа должна проходить не только на уроках математики, но и на уроках труда и особенно на уроках рисования, когда воспроизведение формы предмета зависит от качества и глубины анализа его геометрической формы. Например, при наблюдении куба (или предмета, имеющего форму куба) следует найти в нем характерные точки, отрезки, многоугольники; при наблюдении шара можно обратить внимание на его круглые сечения.

Уже при первоначальном ознакомлении детей с геометрическими фигурами в I классе дети выполняют умственные операции анализа и синтеза. Важной задачей учителя, определяющей методику обучения в этот момент, является анализ фигуры, на основе которого выделяются ее существенные свойства (признаки) и несущественные. Так, например, существенным для треугольника будет не его положение на плоскости (листе бумаги), не относительные размеры сторон, а наличие трех сторон (углов, вершин); для прямоугольника существенно то, что он четырехугольник (четыре угла) и все его углы прямые. Все остальное не существенно.

В процессе обучения возникает потребность применения геометрической и логической терминологии, символики, чертежей. Так, уже во II классе введение буквенной символики помогает не только различать фигуры и их элементы, но и является одним из средств формирования обобщений. Например, запись ОК < 5 см говорит учащимся о том, что отрезок ОК любой отрезок, имеющий длину меньшую, чем 5 см.

Как показывает опыт обучения математике в I-IV классах, под влиянием той легкости и интереса, с которыми учащиеся
I-IV классов воспринимают не только очевидные простые, но иногда трудные геометрические факты, учитель начинает недооценивать наглядный и практический подход к изучению геометрического материала, не выполняет минимума упражнений, помещенных в учебнике, обращает мало внимания на формирование практических навыков. Такой учитель встает на неверный и опасный путь формального ознакомления младших школьников с геометрическими фигурами. Он начинает знакомить детей с фигурами не путем их наблюдения, изготовления из бумаги и вычерчивания, а сообщая формальное определение, только словесным способом.

В процессе определения понятия каждый раз одно понятие (например, «квадрат») определяется через другое, более широкое («прямоугольник»), которое в свою очередь также может быть определено через еще более широкое понятие («параллелограмм», «четырехугольник», «многоугольник»). Такую цепь определений нельзя продолжать бесконечно. В конце концов мы приходим к понятиям, наиболее широким и общим, для которых невозможно указать ближайший род. Такие понятия называют основными (первичными или неопределяемыми).

 

Высокого уровня усвоения достигается при осуществлении связи изучения геометрического материала с другим материалом начального курса математики. В основе этой связи лежит возможность установления отношений между числом и фигурой, свойствами чисел и свойствами фигур. Это позволяет использовать фигуры при формировании понятия числа, свойств чисел, операций над ними и, наоборот, использовать числа для изучения свойств геометрических образов и их отношений.

1. В 1 классе фигуры следует применять наряду с другими материальными вещами как объекты для пересчитывания. Несколько позже такими объектами должны стать элементы фигур, например вершины, стороны, углы многоугольников. Учащиеся постепенно знакомятся с измерением отрезков.

2. Это позволяет устанавливать связь между отрезками и числами. Во II классе устанавливается прямая связь между отрезками (точками) и числами.

3. Геометрические фигуры используются при ознакомлении учащихся с долями. В указанных выше случаях открывается, больше возможностей органически связать изучение геометрических объектов с арифметическим материалом, включенным в курс математики I-IV классов.

Уже в I-IV классах выполняются простейшие классификации углов (прямые и непрямые), многоугольников (по числу углов) и т. д. Изучение родовых и видовых понятий готовит детей к пониманию определений, построенных на указании рода и видовых отличий.

Это дает, например, возможность построить методику ознакомления с прямоугольниками таким образом, что в дальнейшем ученики усваивают, что любой квадрат есть прямоугольник.

4. Использование упражнений, в которых дети отмечают (выделяют) точки, принадлежащие или не принадлежащие фигуре или нескольким фигурам, помогает в дальнейшем трактовать геометрическую фигуру как множество точек.

5. Это позволяет более осознанно выполнять операции деления фигуры на части или получения фигуры из других (складывание), т.е. выполнять по существу операции объединения, пересечения, дополнения над точечными множествами.

Важной общей методической линией осуществления связи в изучении геометрического материала с остальными вопросами курса начальной математики является, таким образом неявная опора на теоретико-множественные и простейшие логико-математические представления в изучении фигур, их отношений, свойств.

6. Общим методическим приемом, обеспечивающим прочные геометрические знания, является формирование пространственных представлений через непосредственное восприятие учащимися конкретных реальных вещей, материальных моделей геометрических образов. В I классе пространственные представления вырабатываются в процессе приобретения детьми практического опыта при изучении отношений взаимного положения предметов, выражаемых словами «выше», «ниже», «справа», «в середине», «слева», «между», «внутри», «вне», «над», «под», «снизу», «сверху», «спереди», «сзади» и т.д. Во II-III классах характер работы по формированию пространственных представлений усложняется. Например, представления об одной фигуре формируется с опорой на другую. Так, опираясь на представления о треугольнике вообще, можно получить представления о прямоугольном треугольнике.

7. Учитель должен систематически проводить работу по формированию умений и навыков применения чертежных и измерительных инструментов, построению изображений геометрических фигур, умений описывать словесно процесс работы, выполняемой учеником, и ее результат, умений применять усвоенную символику и терминологию. Важным методическим условием реализаций этой системы является сначала осознанное выполнение действий и лишь затем автоматизация этих действий.

Результатом обучения в I–IV классах должно быть формирование первоначальных представлений о точности построений и измерений.

В I классе учащиеся овладевают навыками измерения и построения отрезков с помощью линейки (с точностью до 1 см). При этом детям предъявляются не меньшие требования, чем это обычно делается, например, в отношении навыков письма. Во II–IV классах в практику измерений и построений постепенно вводятся новые инструменты: циркуль, циркуль-измеритель, чертежный треугольник, рулетка. Повышаются требования к точности построений и измерений, к качеству чертежей и моделей, выполняемых детьми, к описанию хода и результатов проделанной работы.

Работа по формированию навыков должна проводиться распределение и постепенно почти на каждом уроке (и не только на уроках математики). Это создает условия для более частого применения этих навыков в учебной и практической деятельности, обеспечивает необходимую их прочность.

Для правильного выбора методики обучения младших школьников учитель должен иметь общие представления о системе задач, представленных в учебниках. Эта система включает в каждом классе задачи:

а) в которых геометрические фигуры используются как объекты для пересчитывания (круги, многоугольники, элементы многоугольников). При решении таких задач в основном усваивается необходимая терминология и образуются умения узнавать и различать фигуры;

б) связанные с формированием представлений о геометрических величинах (длине, площади) и навыков измерения отрезков, площадей фигур;

в) вычислительные, связанные с нахождением периметра многоугольников, площади прямоугольника;

г) на элементарные построения геометрических фигур на клетчатой бумаге, на гладкой нелинованной бумаге с помощью линейки, угольника, циркуля (без учета размеров);

д) на элементарные построения фигур с заданными параметрами (треугольник с прямым углом, прямоугольник с заданными сторонами и т.д.);

е) на классификацию фигур;

ж) на деление фигур на части (в том числе на равные части) и на составление фигур из других;

з) связанные с формированием основных навыков чтения геометрических чертежей, использованием буквенных обозначений (формированием «геометрической зоркости»);

Последние изменения программы по математике в начальной школе характеризуются тенденцией усиления внимания к изучению геометрического материала. Так, уже в 1 классе дети знакомятся с такими геометрическими фигурами как точка, линия (прямая, кривая), отрезок, ломаная, многоугольник и его элементы (углы, вершины, стороны), изучение перечисленного геометрического материала не вызывает, как правило, каких либо затруднений у детей.