Ход урока
Актуализация знаний. 1. Устно. Я называю число, а тот, кого спрошу, с него продолжает счет: 5 (6, 7, 8, 9, 10) 3 (4, 5, 6, 7, …) А теперь в обратном порядке: 7 (6, 5, 4, 3, 2, 1) 4 (3, 2, 1) 9 (8, 7, 6, 5, 4, 3, 2, 1) - Как удобно считать – в прямом или обратном порядке? (в прямом) - Почему? (мы так привыкли) - С какого числа мы начинаем счет? (с числа 1) - Возьмите в руки полоски бумаги, образуйте с их помощью цифру 1 и покажите. (Дети берут по 2, 3 палочки, показывают). - Если не догадываются, я их прошу: - А сможете показать цифру 1, используя только одну палочку? (Да, надо ее согнуть). - Какая сначала была полоска? (ровная, прямая) - А какая стала? (кривая) II. Объяснение нового. 1. На доске с двух сторон начерчены прямые и непрямые лини:
– Что начерчено на доске? (разные линии) – А почему – в разных местах? Чем они отличаются? (прямые и кривые). – Кто сможет показать, как я чертила кривые линии? Начертите рядом еще кривые линии. (Дети выходят и мелом чертят их). – А как начертить прямые? (Дети пытаются начертить без линейки – не получается. Постепенно приходят к выводу – нужна линейка). – Кто ответит – при помощи чего вычерчивают прямые и кривые линии? (прямые – при помощи линейки, а кривые – без нее как угодно). – Итак, какие линии мы чертили? (прямые и кривые). 1. Учитель вызывает к доске двух учеников и дает им в руки – концы шнура (или ленты). – Встаньте так, чтобы у вас получилась прямая линия. (Дети, держат шнур за концы и отходят друг от друга так, чтобы шнур был натянут). – А теперь что нужно сделать, чтобы линия получилась кривая? (Нужно приблизиться, шагнуть друг к другу). – Еще раз образуйте прямую линию. (Дети отходят так, чтобы шнур натянулся). 2. Учитель берет в руки ножницы, подходит к детям, которые держат шнур, отрезает его с двух сторон и к месту среза приставляет магнит красного цвета:
Двое детей, стоящие у доски, держат в руках отрезанный шнур и магниты. – Что я сделала со шнуром? (Отрезали). – Была прямая линия. Как ее теперь можно назвать. (Если дети сами не догадываются можно объяснить, что в математике эту фигуру называют отрезок). 3. На магнитной доске учитель крепит два магнита и через них перевешивает нитку.
– При помощи двух магнитов и шнура какую фигуру я смогу изобразить? (Отрезок). – Чтобы начертить на доске кривую – что нам потребуется в помощь? (Мел). – Что еще нужно, чтобы начертить прямую? (Мел, линейка). – А как мне начертить прямую? Это часть прямой или кривой линии? (Часть прямой). – Что еще мы делали с прямой линией, когда из нее образовывали отрезок? (Мы ее отрезали и на место показывали магнитом). – Как это сделать на доске? Что поставим вместо магнита? (Точки). – Сколько точек нужно поставить, чтобы провести один отрезок? (Одна, две). Дети по очереди выходят к доске и пробуют начертить отрезок, постепенно приходят к выводу, что нужно две точки, чтобы через них провести один отрезок. – У себя в тетради поставьте одну точку и через нее проведите отрезки. Сколько их получилось? (У детей получается разное количество лучей, прямых). – А теперь – ниже поставьте две точки и проведите через них отрезки. Сколько их получилось? (Одна). III. Итог урока. У вас на столе полоски бумаги. Покажите самую длинную из них. (Дети поднимают ее, показывают учителю). – Какая это линия – прямая или кривая? (Прямая). – Как из нее получить кривую? (Согнуть). – На концах полоски красным карандашом поставьте точки. Какая фигура получилась? (Отрезок). – Итак, какие новые фигуры мы сегодня узнали? (Прямая, кривая, отрезок). Во 2 классе дети знакомятся с такими геометрическими фигурами, как угол, прямоугольник, квадрат и их свойствами. Опишем методику изучения этих фигур более подробно. Прямой угол Понятие прямого угла носит не столько самостоятельную, сколько вспомогательную роль – подготовить детей к введению понятий прямоугольника и квадрата. По традиционной программе в начальной школе дети знакомятся с двумя видами углов: прямые и непрямые. В большинстве авторских программ (Н.Б. Истоминой, И.И. Аргинская, Л.Г. Петерсон и др.) кроме прямых особо выделяются острые и тупые углы:
С углом, как составной частью многоугольника, дети знакомятся еще с 1 класса. Основная задача на данном этапе – сформировать представление о прямом угле. Это можно сделать следующим образом. Предложите ребенку взять несколько листов бумаги и каждый из них дважды сложить пополам («уголком»). Сравнивая после этого полученные углы между собой путем их наложения друг на друга, приходим к выводу, что все они равны, независимо от того, в каком направлении мы перегибали листы. Полученный угол называется прямым. Сформировав представление о прямом угле, необходимо научить ребенка находить прямые углы как в окружающей обстановке (углы стола, окна, стены и т.д.), так и в составе геометрических фигур (различного вида многоугольников). В случае затруднения визуального определения («на глаз»), в качестве эталона используется прямой угол стандартного прямоугольного треугольника. После того, как данное умение сформировано, можно переходить к знакомству с прямоугольником. Прямоугольник Для знакомства с прямоугольником предварительно заготовьте 8-9 четырехугольников, вырезав их из цветной бумаги так, чтобы среди них было 3-4 прямоугольника с разным соответствием сторон.
Предложите ребенку с помощью эталона определить, сколько в каждом четырехугольнике прямых углов, и полученное число записать на каждой фигуре. Попросите показать четырехугольники, у которых только один прямой угол, два прямых угла, совсем нет прямых углов. Есть ли четырехугольники, у которых все углы прямые? Отложите их в сторону. Четырехугольники, у которых все углы прямые, называются прямоугольниками. Таким образом, у понятия «прямоугольник» два существенных признака: 1) это должен быть четырехугольник; 2) у него все углы должны быть прямыми. Если хотя бы один из этих признаков не выполняется, то данная фигура не является прямоугольником. Знакомство с квадратом осуществляется так же, как и с прямоугольником. Заготовьте заранее 7-8 прямоугольников, среди которых 2-3 квадрата. Предложите ребенку самому определить, какие из предложенных фигур чем-то отличаются от остальных. Если это задание вызовет затруднение, попросите сравнить длины сторон каждого прямоугольника. Тем самым из всего класса прямоугольников будут выделены те, у которых все стороны равны. Такие прямоугольники называются квадратами. Таким образом, у понятия «квадрат» два существенных признака: 1) это прямоугольник; 2) у него все стороны равны. Замечание. Сложность в соотнесении понятий «прямоугольник» и «квадрат» состоит в том, что квадрат является частным случаем прямоугольника. По этой причине дети не видят в квадрате прямоугольник. В этом можно убедиться на простом примере. Предложите ребенку посчитать, сколько прямоугольников в следующей фигуре:
Некоторые дети видят в ней 2 прямоугольника, другие – три (кроме двух маленьких, еще – самый большой), третьи – обнаруживают, что два маленьких вместе тоже составляют прямоугольник. Однако не все дети видят прямоугольник в расположенном слева квадрате. Попытка взрослого обратить на это внимание нередко вызывает возражение со стороны ребенка, убежденного в том, что это не прямоугольник, а квадрат. Логические аргументы тоже не всегда помогают. Приведем типичный диалог. – Давай рассуждать так, – предлагает взрослый. – Что такое прямоугольник? – Это четырехугольник, у которого все углы прямые, – заученно отвечает ребенок. – Эта фигура четырехугольник? – спрашивает взрослый, показывая на квадрат. – Да, – соглашается тот, еще не понимая, к чему клонит взрослый. – У него все углы прямые? – Все, – внимательно осмотрев рисунок, подтверждает ребенок. – Значит это прямоугольник? – задает последний вопрос взрослый, уверенный в том, что сила логики наконец-то восторжествует. – Нет, это квадрат, – с безмятежной внутренней уверенностью отвечает тот. Этот феномен свидетельствует о том, что многие дети данного возраста в своих суждениях опираются не на логические законы, а на внешнее восприятие, которое для них выступает более убедительным аргументом.
1.7. МЕТОДИКА ИЗУЧЕНИЯ АЛГЕБРАИЧЕСКОГО МАТЕРИАЛА План: 1. Цели изучения алгебраического материала в начальных классах. 2. Свойства арифметических действий, изучаемые в начальных классах. 3. Изучение числовых выражений и правил порядка выполнения действий: - одного порядка без скобок; - одного порядка со скобками; - выражения без скобок, включающие 4 арифметических действия, со скобками. 4. Анализ числовых равенств и неравенств, изучаемых в начальных классах (сравнение двух чисел, числа и числового выражения, двух числовых выражений). 5. Введение буквенной символики с переменной. 6. Методика изучения уравнений: а) дайте определение уравнения (из лекций по математике и из учебника математики для начальной школы), б) выделите объем и содержание понятия, в) каким методом (абстрактно-дедуктивным или конкретно-индуктивным) будете вводить это понятие? Опишите основные этапы работы над уравнением.
Выполните задания: 1. Объяснить целесообразность использования в начальных классах неравенств с переменной. 2. Подготовить сообщение к занятию о возможности формирования у учащихся функциональной пропедевтики (через игру, через изучение неравенств). 3. Подобрать задания для учащихся по выполнению существенных и несущественных свойств понятия «уравнение». Рекомендательная литература 1. Абрамова О.А., Моро М.И. Решение уравнений // Начальная школа. – 1983. – № 3. – С. 78-79. 2. Ыманбекова П. Средства наглядности при формировании понятия «равенство» и «неравенство» // Начальная школа. – 1978. – № 11. – С. 38-40. 3. Щадрова И.В. О порядке действий в арифметическом выражении // Начальная школа. – 2000. – № 2. – С. 105-107. 4. Шихалиев Х.Ш. Единый подход к решению уравнений и неравенств // Начальная школа. – 1989. – № 8. – С. 83-86. 5. Назарова И.Н. Ознакомление с функциональной зависимостью при обучении решению задач // Начальная школа. – 1989. – № 1. – С. 42-46. 6. Кузнецова В.И. О некоторых типичных ошибках учащихся, связанных с вопросами алгебраической пропедевтики // Начальная школа. – 1974. – № 2. – С. 31. Общая характеристика методики изучения Введение алгебраического материала в начальный курс математики позволяет подготовить учащихся к изучению основных понятий современной математики, например таких, как «переменная», «уравнение», «неравенство» и др., способствует развитию у детей функционального мышления. Основные понятия темы – «выражение», «равенство», «неравенство», «уравнение». Термин «уравнение» вводится при изучении темы «Тысяча», но подготовительная работа к ознакомлению учащихся с уравнениями начинается с 1 класса. Термины «выражение», «значение выражения», «равенство», «неравенство» включаются в словарь учащихся начиная со 2 класса. Понятие «решить неравенство» в начальных классах не вводится. Числовые выражения В математике под выражением понимают постоянную по определенным правилам последовательность математических символов, обозначающих числа и действия над ними. Примеры выражений: 7; 5 + 4; 5 · (3 + в); 40: 5 + 6 и т.п. Выражения вида 7; 5 + 4; 10: 5 + 6; (5 + 3) · 10 называют числовыми выражениями в отличие от выражений вида 8 – а; (3 + в); 50: к, называемых буквенными выражениями или выражениями с переменной. Задачи изучения темы 1. Научить учащихся читать простейшие выражения. 2. Познакомить учащихся с правилами порядка выполнения действий над числами и в соответствии с ними выработать умение находить числовые значения выражений. 3. Познакомить учащихся с тождественными преобразованиями выражений на основе арифметических действий. В методике ознакомления младших школьников с понятием числового выражения можно выделить три этапа, предусматривающие ознакомление с выражениями, содержащими: - одно арифметическое действие (I этап); - два и более арифметических действий одной ступени (II этап); - два и более арифметических действий разных ступеней (III этап). С простейшими выражениями – суммой и разностью – учащихся знакомят в I классе (при изучении сложения и вычитания в пределах 10); с произведением и частным двух чисел – во II классе. Уже при изучении темы «Десяток» в словарь учащихся вводятся названия арифметических действий, термины «слагаемое», «сумма», «уменьшаемое», «вычитаемое», «разность». Помимо терминологии, они должны также усвоить и некоторые элементы математической символики, в частности знаки действий (плюс, минус); они должны научиться читать и записывать простейшие математические выражения вида 5 + 4 (сумма чисел «пять» и «четыре»); 7 – 2 (разность чисел «семь» и «два»). Сначала учащиеся знакомятся с термином «сумма» в значении числа, являющегося результатом действия сложения, а затем в значении выражения. Прием вычитания вида 10 – 7, 9 – 6 и т.п. основан на знании связи между сложением и вычитанием. Поэтому необходимо научить детей представлять число (уменьшаемое) в виде суммы двух слагаемых (10 – это сумма чисел 7 и 3; 9 – это сумма чисел 6 и 3). С выражениями, содержащими два и более арифметических действий, дети знакомятся на первом году обучения при усвоении вычислительных приемов ± 2, ± 3, ± 1. они решают примеры вида 3 + 1 + 1, 6 – 1 – 1, 2 + 2 + 2 и др. Вычисляя, например, значение первого выражения, ученик поясняет: «К трем прибавить один, получится четыре, к четырем прибавить один, получится пять». Аналогичным образом поясняется решение примеров вида 6 – 1 – 1 и др. Тем самым первоклассники постепенно готовятся к выводу правила о порядке выполнения действий в выражениях, содержащих действия одной ступени, которое обобщается во II классе. В I классе дети практически овладеют и другим правилом порядка выполнения действий, а именно выполнения действий в выражениях вида 8 – (4 + 2); (6 - 2) + 3 и др. Обобщаются знания учащихся о правилах порядка выполнения действий и вводится еще одно правило о порядке выполнения действий в выражениях, не имеющих скобок и содержащих арифметические действия разных ступеней: сложение, вычитание, умножение и деление. При ознакомлении с новым правилом о порядке выполнения действий работу можно организовать по-разному. Можно предложить детям прочитать правило по учебнику и применить его при вычислении значений соответствующих выражений. Можно также предложить учащимся вычислить, например, значение выражения 40 – 10: 2. ответы могут получиться разными: у одних значение выражения окажется равным 15 у других 35. После этого учитель поясняет: «Чтобы найти значение выражения, не имеющего скобок и содержащего действия сложения, вычитания, умножения и деления, надо выполнить по порядку (слева направо) сначала действия умножения и деления, а затем (также слева направо) сложения и вычитания. В данном выражении надо сначала 10 разделить на 2, а затем из 40 вычесть полученный результат 5. значение выражения равно 35». Учащиеся начальных классов фактически знакомятся с тождественными преобразованиями выражений. Тождественное преобразование выражений – это замена данного выражения другим, значение которого равно значению заданного (термин и определение учащимся начальных классов не даются). С преобразованием выражений учащиеся встречаются с 1 класса в связи с изучением свойств арифметических действий. Например, при решении примеров вида 10 + (50 + 3) удобным способом дети рассуждают так: «Удобнее десятки сложить с десятками и к полученному результату 60 прибавить 3 единицы. Запишу: 10+(50 + 3) = (10 + 50) + 3 = 63». Выполняя задание, в котором надо закончить запись: При преобразовании выражений учащиеся иногда допускают ошибки вида (10 + 4) · 3 = 10 · 3 + 4. причина подобного рода ошибок связана с неправильным использованием ранее усвоенных знаний (в данном случае с использованием правила прибавления к сумме числа при решении примера, в котором сумму надо умножить на число). Для предупреждения таких ошибок можно предложить учащимся следующие задания: а) Сравни выражения, записанные в левой части равенств. Чем они похожи, чем отличаются? Объясни, как вычислили их значения: (10 + 4) + 3 = 10 + (4 + 3) = 10 + 7 = 17 (10 + 4) · 3 = 10 · 3 + 4 · 3 = 30 + 12 = 42 б) Заполни пропуски и найди результат: (20 + 3) + 5 = 20 + (3 + ð); (20 + 3) · 5 = 20 · ð + 3 · ð. в) Сравни выражения и поставь между ними знак >,< или =: (30 + 4) + 2 … 30 + (4 + 2); (30 + 4) + 2 … 30 · 2 + 4 · 2. г) Проверь вычислением, верны ли следующие равенства: 8 · 3 + 7 · 3 = (8 + 7) · 3; 30 + (5 + 7) = 30 + 7. Буквенные выражения В начальных классах предусматривается проведение – в тесной связи с изучением нумерации и арифметических действий – подготовительной работы по раскрытию смысла переменной. С этой целью в учебники математики включаются упражнения, в которых переменная обозначается «окошком». Например, ð < 3, 6 < ð, ð + 2 = 5 и др. Здесь важно побуждать учащихся к тому, чтобы они стремились подставить в «окошко» не одно, а поочередно несколько чисел, проверяя каждый раз, верная ли получатся запись. Так, в случае ð < 3 в «окошко» можно подставить числа 0, 1, 2; в случае 6 < ð - числа 7, 8, 9, 10, 20 и др.; в случае В целях упрощения программы по математике для начальных классов и обеспечения ее доступности буквенная символика как средство обобщения арифметических знаний не используется. Все буквенные обозначения заменяются словесными формулировками. Например, вместо задания
Предлагается задание в такой форме: «Увеличь число 3 в 4 раза; в 5 раз; в 6 раз; …». Равенства и неравенства Ознакомление учащихся начальных классов с равенствами и неравенствами связано с решением следующих задач: - научить устанавливать отношение «больше», «меньше» или «равно» между выражениями и записывать результаты сравнения с помощью знака; - научить читать равенства и неравенства. Методика формирования у младших школьников представлений о числовых равенствах и неравенствах предусматривает следующую этапность работы. На I этапе, в первую очередь учебную неделю, первоклассники выполняют упражнения на сравнение совокупностей предметов. Здесь целесообразнее всего использовать прием установления взаимно однозначного соответствия. На этом этапе результаты сравнения еще не записываются с помощью соответствующих знаков отношения. На II этапе учащиеся выполняют сравнение чисел, сначала опираясь на предметную наглядность, а затем на то свойство чисел натурального ряда, в соответствии с которым из двух различных чисел то число больше, которое при счете называют позже, и то число меньше, которое называют раньше. Установленные таким образом отношения дети записывают с помощью соответствующих знаков. Например, 3 > 2, 2 < 3. В дальнейшем при изучении нумерации (в концентрах «Сотня», «Тысяча», «Многозначные числа») для сравнения чисел полезно применять два способа, а именно устанавливать отношения между числами: 1) по месту их расположения в натуральном ряду; 2) на основе сравнения соответствующих разрядных чисел, начиная с высших разрядов. Например, 826 < 829, так как сотен и десятков в этих числах поровну, а единиц в первом числе меньше, чем во втором. Так же можно сравнивать величины: 4 дм 5 см > 4 дм 3 см, так как дециметров больше, чем во второй. Кроме того, величины можно сначала выразить в единицах одного измерения и уже после этого сравнивать их: 45 см > 43 см. Подобные упражнения вводятся уже при изучении сложения и вычитания в пределах 10. Их полезно выполнять с опорой на наглядность, например: учащиеся выкладывают на партах слева четыре кружка, а справа четыре треугольника. Выясняется, что фигур поровну – по четыре. Записывают равенство: 4 = 4ывают сумму 4 + 1. Слева фигур больше, чем справа, значит, 4 + 1 > 4. Используя прием уравнения, учащиеся переходят от неравенства к равенству. Например, на наборное полотно ставят 3 гриба и 4 белочки. Чтобы грибов и белочек было поровну, можно добавить один гриб (тогда будет 4 гриба и 4 белочки).
На наборном полотне 5 легковых и 5 грузовых машин. Чтобы одних машин было больше, чем других, можно: 1) убрать одну (две, три) машину (легковую или грузовую) или 2) добавить одну (две, три) машину.
Постепенно при сравнении выражений дети переходят от опоры на наглядность к сравнению их значений. Этот способ в начальных классах является основным. При сравнении выражений учащиеся могут также опираться и на знания: а) взаимосвязи между компонентами и результатом арифметического действия: 20 + 5 · 20 + 6 (слева записана сумма чисел 20 и 5, справа – сумма чисел 20 и 6. Первые слагаемые этих сумм одинаковые, второе слагаемое суммы слева меньше, чем второе слагаемое суммы справа, значит, сумма слева меньше, чем сумма справа: 20 + 5 < 20 + 6; б) отношение между результатами и компонентами арифметических действий: 15 + 2 · 15 (слева и справа сначала было поровну – по 15. Затем к 15 прибавили 2, стало больше, чем 15); в) смысла действия умножения: 5 + 5 + 5 + 5 + 5 · 5 · 3 (слева число 5 взяли слагаемым 5 раз, справа число 5 взяли слагаемым 3 раза, значит, сумма слева будет больше, чем справа: 5 + 5 + 5 + 5 + 5 > 5 + 5 + 5); г) свойств арифметических действий: (5 + 2) · 3 · 5 · 3 + 2 · 3 (слева сумму чисел 5 и 2 умножают на число 3, справа находят произведения каждого слагаемого на число 3 и складывают их. Значит, вместо звездочки можно поставить знак «равно»: В этих случаях вычисления значений выражений используются для проверки правильности постановки знака. Для записи неравенств с переменной в начальных классах используется «окошко»: 2 > ð, ð = 5, ð > 3. Первые упражнения такого вида полезно выполнять с опорой на числовой ряд, обращаясь к которому учащиеся замечают, что число 2 больше единицы и нуля, поэтому в «окошко» Аналогично выполняются и другие упражнения с окошком.
Основным способом при рассмотрении неравенств с переменной является способ подбора. Для облегчения значений переменной в неравенствах предлагается выбирать их из конкретного ряда чисел. Например, можно предложить выписать те из данных чисел ряда 7, 8, 9, 10, 11, 12, 13, 14, при которых верна запись ð - 7 < 5. При выполнении данного задания ученик может рассуждать так: «Подставим в «окошко» число 7: 7 минус 7 будет 0, 0 меньше 5, значит число 7 подходит. Подставим в «окошко» число 8:8 минус 7 получится 1, 1 меньше 5, значит, число 8 тоже подходит … Подставим в «окошко» число 12:12 минус 7 получится 5, 5 меньше 5 – неверно, значит число 12 не подходит. Чтобы запись ð - 7 < 5 была верной, в «окошко» можно подставить любое из чисел 7, 8, 9, 10, 11». Уравнения В конце 3 класса дети знакомятся с простейшими уравнениями вида: х + 8 = 15; 5 + х = 12; х – 9 = 4; 13 – х = 6; х · 7 = 42; 4 · х = 12; х: 8 = 7; 72: х = 12. Ребенок должен уметь решать уравнения двумя способами: 1) способом подбора (в простейших случаях); 2) способом, основанным на применении правил нахождения неизвестных компонентов арифметических действий. Приведем пример записи решения уравнения вместе с проверкой и рассуждений ребенка при его решении:
«В уравнении х – 9 = 4 икс стоит на месте уменьшаемого. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое (х = 4 + 9). Проверим: из 13 вычтем 9, получим 4. получилось верное равенство 4 = 4, значит уравнение решено правильно». В 4 классе ребенка можно познакомить с решением простых задач способом составления уравнения. 1.8. ИЗУЧЕНИЕ ДОЛЕЙ Согласно программе начального курса математики при изучении темы «Доли» ставятся следующие задачи сформировать у учащихся представление о доле величины, научить сравнивать доли одной и той же величины на наглядной основе, решать задачи на нахождение доли числа и числа по его доле. Термины дробь, числитель, знаменатель не используются при изучении названной темы. С целью расширения математического кругозора учащихся при изучении темы «Доли» мы ввели термины дробь, числитель, знаменатель, рассмотрели образование, чтение, запись и сравнение дробей с числителем, большим единицы. Остановимся подробнее на методике проведенной работы. Для формирования представления о дроби использовалось решение текстовых задач. Первой учащимся была предложена задача: Два брата разделили поровну между собой 6 яблок. Сколько яблок досталось каждому брату? Ученики самостоятельно записывают решение задачи Далее предлагается следующая задача: «Два брата разделили между собой одно яблоко поровну. Сколько яблок досталось каждому брату?» Учитель берет яблоко и просит разделить его между братьями поровну. Как поступить в данном случае? Ученики предлагают разрезать яблоко на две равные части. Учитель разрезает яблоко, показывает одну из равных частей и спрашивает: - Как можно назвать эту часть яблока? (Половина.) - Почему? (Яблоко разделили пополам.) - Кто догадался, как можно по-другому назвать половину? (Одна вторая.) - Докажите. (Яблоко разделили на две равные части и взяли одну из частей.) Учитель показывает вторую часть яблока и предлагает учащимся назвать ее: - Вспомните вопрос задачи и ответьте на него. (Каждому брату досталась половина яблока или одна вторая яблока.) – Одна вторая – это дробное число, оно записывается так: Далее поясняется, что в записи дроби Затем для решения предлагается задача: «Три брата разделил между собой одно яблоко поровну. Сколько досталось яблок каждому брату?» Учащиеся самостоятельно записывают решение этой задачи, формулируют ответ на ее вопрос, выясняют значение числителя и знаменателя дроби одна третья. Чтобы научить детей сравнивать дроби (доли) на основе наглядности, мы использовали учебное задание с элементами самоконтроля. На доске расположены шесть карточек, на которых изображены одинаковые квадраты, разделенные на равные части различным образом. Квадраты расположены в следующем порядке:
Учитель задает вопросы: какие фигуры изображены? Что общего у всех этих квадратов? Просит учащихся разбить квадраты на группы и объяснить, по какому признаку они это сделали. На доске получилась иллюстрация:
Учитель предлагает: - Рассмотрите первую пару квадратов и скажите, какая часть каждого квадрата заштрихована. Покажите одну вторую первого квадрата. Обозначьте дробью. Что обозначает знаменатель этой дроби? Что обозначает числитель этой дроби? Покажите одну вторую другого квадрата. Обозначьте дробью. Сравните заштрихованные части этих квадратов. Запишите числовое равенство. Учитель показывает, как правильно оформить запись: \ = \ Аналогичная работа проводится с остальными парами квадратов. Затем квадраты расставляются в такой последовательности:
Ученикам предлагается поменять местами карточки, на которых изображены равные дроби. Если задание будет выполнено правильно, они прочитают слово клюква – ответ к загадке: Когда весною талые сойдут с болот снега. Она как бусы алые усеет берега. Данное учебное задание ученики выполняют с интересом. Повышенную активность, даже у слабых учеников, вызывает вторая часть задания. Для формирования умения сравнивать дроби предлагаются учебные задания с элементами занимательности и самоконтроля. Приведем одно из заданий. На доске прикреплены модели кругов, разделенных на две, на восемь, на шесть, на четыре, на три равные части:
Работа проходит следующим образом: - Какие геометрические фигуры перед вами? Что общего у всех этих кругов? Посмотрите на первый круг слева. На сколько равных частей он разделен? Покажите заштрихованную часть круга. Какая это часть круга? Запишите соответствующую дробь под этим кругом. На сколько равных частей разделен следующий круг? Покажите заштрихованную часть круга. Какая это часть? Запишите соответствующую дробь под кругом. Что обозначает знаменатель этой дроби, что обозначает числитель этой дроби? Аналогичная работа проводится с остальными кругами. Далее предлагается таблица:
Используя эту таблицу, учащиеся заменяют дроби буквами и отгадывают загадку «Не куст, а с листочками, не рубашка, а сшита, не человек, а говорит». Затем на доске дается запись:
Используя в качестве наглядности круги, требуется поставить вместо «и» соответствующие знаки сравнения. Учащиеся выполняют это задание самостоятельно, а затем проводят проверку у доски. Убедившись в том, что у учеников сформировались представление о дроби и умение сравнивать дроби с опорой на наглядность, мы решили ввести дроби с числителем, большим единицы. Для этого предлагаем решить следующую задачу:
Для решения этой задачи используем наглядный материал круг; разделенный на десять равных частей. Работа над задачей проходит так: - На сколько равных кусков мама разрезала торт? Сколько торта съела сестра? Покажите на рисунке. Какую часть торта составляет один кусок? Кто может записать соответствующую дробь?
- Сколько кусков торта съел брат? Покажите на рисунке. Какую часть торта составляют два куска? Кто сможет записать дробь две десятых? Этот вопрос сначала вызывает затруднение, однако поразмыслив, многие приходят к верному выводу и записывают: - Назовите знаменатель этой дроби. Объясните, что он означает. Назовите числитель этой дроби. Объясните его значение. Затем учащиеся выполняют сравнение дробей с опорой на наглядность и записывают соответствующие неравенства: - Кому из детей досталось больше торта? А кому меньше? Сколько всего кусков торта съели дети? Покажите на рисунке. Какую часть торта составляют три куска? Запишите дробь. Объясните значение числителя и знаменателя этой дроби. Выполнение этого задания вызывает интерес даже у малоактивных детей. В работе принимают участие все ученики класса. Далее ведется работа по изучению тем «Нахождение доли числа» и «Нахождение числа по доле». Обе эти темы мы ввели одновременно. Причем первой решалась задача, в которой требовалось по доле найти число. Затем предлагалось составить обратную задачу, т.е. найти долю числа. Деятельность учащихся была организована следующим образом. Вначале учащимся была предложена задача:
|









 Запишите решение задачи. На доске оформляется запись:
Запишите решение задачи. На доске оформляется запись: 




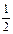
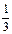
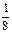

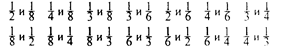
 «Мама к чаю подала торт, разрезанный на десять равных кусков. Брат съел два куска торта, а сестра один кусок. Какую часть торта съел брат? Какую часть торта съела сестра?»
«Мама к чаю подала торт, разрезанный на десять равных кусков. Брат съел два куска торта, а сестра один кусок. Какую часть торта съел брат? Какую часть торта съела сестра?» Все ученики записывают дробь правильно.
Все ученики записывают дробь правильно. .
.



