Тема: Методика изучения длины

План:

1. Порядок изучения темы:

а) подготовительный этап;

б) ознакомление с понятием «длина»;

в) введение первой единицы измерения длины «сантиметр» и обучение измерению длины с помощью линейки;

г) упражнения на закрепление [13];

д) ознакомление с дециметром (упражнения на закрепление);

е) ознакомление с метром (упражнения на закрепление);

ж) ознакомление с километром (выписать задания на измерение расстояний).

2. Сделать анализ наглядных пособий.

3. По каждому пункту найти ответ по учебникам математики.

4. Приведите примеры упражнений, используемых для раскрытия свойств величин.

 

Рекомендательная литература

1. Король Я.А. Измерение длины отрезков // Начальная школа. – 1982. – № 10. – С. 51-53.

2. Холомкина А.И. Изучение мер длины в 1-2-х классах // Начальная школа. – 1981. – № 9. – С. 37-41.

 

В начальной школе дети знакомятся с четырьмя основными величинами (длина, масса, время, площадь). В 1 классе начинается систематическое изучение длины и осуществляется первичное знакомство со временем. Рассмотрим более подробно методику работы над длиной.

 

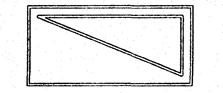
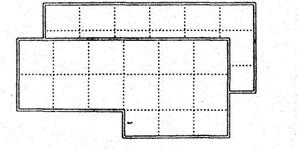
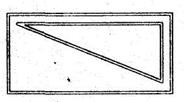
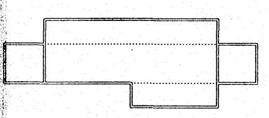
В методике работы над длиной можно выделить несколько самостоятельных этапов.

На первом этапе уточняются уже имеющиеся у ребенка представления о длине и термин «длина» вводится в его активный словарь. Для этого используется метод приложения одного предмета линейной протяженности к другому (например, карандаша к ручке). Как правило, результат этого сравнения ребенок уже может выразить с помощью слова «длина». Если же в его речи доминирует более широкий термин «больше», то его можно дифференцировать: «В этом случае говорят, что длина карандаша больше, чем длина ручки». Таким образом, смысл термина «длина» у ребенка ассоциируется с линейной протяженностью предмета. Чем предмет протяженнее, тем его длина больше.

На втором этапе моделируется ситуация, в которой предыдущий прием сравнения путем приложения одного предмета к другому уже не срабатывает. Дл этого можно на разных краях стола положить две полоски бумаги примерно одинаковой длины (чтобы их было трудно сравнить «на глаз») и попросить ребенка сравнить их длины, соблюдая условие: приближать полоски друг к другу нельзя. После ряда попыток совместно с ребенком выводим несколько новых приемов сравнения длин: а) с помощью веревочки (прикладывая ее сначала к одной полоске, а затем к другой); б) с помощью короткой полоски-мерки, укладывая ее сначала вдоль первой полоски, а затем вдоль второй; в) наконец, можно перевернуть полоски обратной стороной и пересчитать на них заранее нанесенные через один и тот же промежуток метки (если, например, в первой полоске таких меток 8, а во второй 9, то длина второй полоски больше, чем первой).

На третьем этапе сначала пересчитываем метки на полосках (например, на первой полоске таких меток 15, а на второй – 16). Делаем вывод: длина второй полоски больше. Однако прикладывая ее к первой, убеждаемся, что она наоборот, короче первой. В чем же дело? Оказывается метки на полосках нанесены через промежутки различной длины, т.е. мерки разные. Вывод: при сравнении длин нужно пользоваться одинаковыми мерками. Тем самым мотивируется введение стандартной единицы измерения длины – 1 см. В качестве материального носителя этой единицы длины удобно использовать модель вырезанного из картона квадратика со стороной 1 см.

На четвертом этапе ребенку можно предложить измерить длину нескольких предметов, выкладывая вдоль них модели квадратиков со стороной 1 см. Тем самым будет раскрыт смысл измерения величины как процесса ее сравнения с однородной величиной, принятой за единицу измерения. При этом можно подвести ребенка к самостоятельному выводу, что результат измерения от того, какая мерка для этого была выбрана.

На пятом этапе знакомим ребенка с линейкой как инструментом, с помощью которого измеряется длина. В соответствии с последними изменениями программы, в содержание 1 класса вновь включено понятие отрезка. Поэтому уже в 1 классе отрезок начинает выполнять роль «геометрического носителя», на котором отрабатывается умение измерять длину отрезка. Это умение в дальнейшем будет востребовано при вычислении периметра и площади многоугольника.

На заключительном этапе, в конце учебного года, вводится вторая единица измерения длины – дециметр. Необходимость введения новой единицы мотивируется неудобством использования сантиметра при измерении больших расстояний (например, длины крышки стола). С помощью дециметра этот процесс осуществляется быстрее. Вводится соотношение между этими единицами: 1 дм = 10 см. на данном этапе основная функция изучения этих единиц измерения длины состоит в том, чтобы способствовать усвоению нумерации чисел второго десятка. Ведь дециметр – это хорошая модель десятка, а сантиметр – единицы. Поэтому перевод одной единицы измерения в другую обогащает опыт ребенка при изучении разрядного состава двузначных чисел в пределах 20.

Таким образом, заканчивая 1 класс, ребенок должен иметь представления о длине как одной из величин, понимать смысл измерения длины как процесса сравнения ее с однородной величиной, принятой за единицу измерения, знать две единицы измерения длины (сантиметр и дециметр) и соотношение между ними, уметь измерять длины конкретных предметов и отрезков.

Такая величина как время, в 1 классе вводится только в ознакомительном порядке. Ребенок должен научиться определять время по часам с точностью до часа (минута и ее соотношение с часом по программе не вводится).

Проверочные задания по теме «Изучение величин»

1) Поставь знаки >, < или =:

1 дм …3 см; 8 см …2 дм; 1 дм 4 см …15 см.

2) Впиши нужные числа:

1 дм = … см; 1 дм 7 см = … см; 19 см = … дм … см.

Во в 2 классе продолжается работа над такими величинами как длина, время, масса.

При изучении длины водится третья единица измерения – метр. Потребность в обращении к этой единице мотивируется неудобством прежних единиц (сантиметра и дециметра) при измерении больших расстояний (например, длины класса). Кроме того, все три единицы активно используются при изучении нумерации чисел в пределах ста (2 класс) и в пределах тысячи (3 класс). Метр в этом отношении может рассматриваться в качестве модели сотни, дециметр – модели десятка, а сантиметр – модели единицы. Перевод одних единиц измерения в другие служит для ребенка хорошей практикой в усвоении разрядного состава двузначных и трехзначных чисел. Уже на данном этапе ребенок усваивает соотношение между изученными единицами длины:

1 дм = 10 см; 1 м = 10 дм; 1 м = 100 см.

В изучении другой величины – времени – в качестве новой единицы измерения выступает минута. Ребенок должен уметь определять время по часам уже с точностью до минуты. Так как 1 ч = 60 мин, то перевод составных единиц в простые и обратно (например, 1 ч 28 мин = 88 мин; 92 мин = 1 ч 32 мин и др.) также помогает в усвоении разрядного состава двузначных чисел. Однако в отличие от единицы длины, в изучении мер времени есть одна особенность: в ее основе лежит шестидесятеричная система счисления. Это является причиной одной из самых распространенных ошибок при работе с мерами времени, когда при переводе часа в минуты ребенок считает, что 1 ч = 100 мин. Поэтому на данный факт следует обратить особое внимание.

 

Тема: Методика изучения темы «Площадь»

План:

1. Методика изучения темы «Площадь»:

а) подготовительный этап;

б) ознакомление с понятием «площадь»;

в) введение первой единицы измерения площади «квадратный сантиметр»;

г) обучение измерению площади с помощью палетки;

д) методика ознакомления с правилами вычисления площади прямоугольника;

е) закрепление (выписать наиболее значимые упражнения);

ж) ознакомление с квадратным дециметром;

з) ознакомление с квадратным метром.

Выполнить задания:

1. По каждому из пунктов составить фрагменты уроков, подготовиться к их проведению.

 

Рекомендательная литература

1. Царева С.Е. Первые уроки по изучению площади // Начальная школа. – 1981. – № 10. – С. 39-42.

2. Абдуллаев К.О. О подготовке учащихся к усвоению понятия площади // Начальная школа. – 1978. – № 9. – С. 17-20.

3. Салихова М.О. О дифференциации понятия «периметр» и «площадь» фигуры // Начальная школа. – 1981. – №10. – С. 42-44.

Площадь фигуры, единицы измерения

Данную тему изучают в следующей последовательности.

1) Уточнение представлений о площади. Для этого можно взять две плоские фигуры и наложить одну на другую так, чтобы первая целиком помещалась во второй.

В этом случае говорят, что площадь первой фигуры меньше площади второй фигуры.

2) Моделируется ситуация, когда ни одна из плоских фигур в другой целиком не помещается (т.е. метод наложения, который использован на предыдущем этапе, уже не работает). Как быть в этом случае? Для этого фигуры предварительно с обратной стороны расчерчиваются на одинаковые квадратики. Переворачиваем и подсчитываем квадратики в каждой фигуре. Та фигура, в которой количество квадратиков больше, имеет большую площадь.

3) На данном этапе моделируется ситуация, которая похожа на предыдущую. Однако в ней первая фигура хотя и имеет больше квадратиков, но целиком помещается во второй. Как такое могло произойти? Причина в том, что во второй фигуре квадратики большего размера. Вывод: для сравнения площадей нужны одинаковые квадратики. Этим мотивируется введение стандартной единицы измерения площади – 1 см².

4) Измерение площади произвольной фигуры с помощью пленки на ней сеткой квадратных сантиметров.

5) Изучение правила вычисления площади прямоугольника.

6) Введение новых единиц измерения площади – 1 дм² и 1 м². Необходимость введения этих единиц мотивируется тем, что квадратным сантиметром измерять площади больших фигур неудобно. Особое внимание следует обратить на соотношение квадратных единиц, т.к. дети его часто путают с соотношением линейных единиц.

Рассмотрим один из подходов, основанного на выполнении практических заданий учащимися.

Одной из задач изучения геометрического материала в начальной школе является формирование у учащихся общих представлений о площади и выработка умения находить площадь фигуры. На практике часто овладение младшими школьниками этим умением оказывается формальным.

Для формирования осознанного умения определять площадь прямоугольника очень важны первые уроки по изучению площади. Недостаточное внимание учителей на этих уроках к упражнениям, направленным на обеспечение понимания детьми конкретного смысла измерения площади, является, на наш взгляд одной из причин отмеченного недостатка в знаниях учащихся.

На вопрос «Что значит измерить площадь прямоугольника?» дети чаще всего отвечают так: «Это значит, что нужно измерить длину и ширину прямоугольника и найти произведение полученных чисел». Но ведь найти площадь прямоугольника (в квадратных сантиметрах) – это значит определить, сколько квадратных сантиметров содержится в нем. Учащиеся смешивают понятие измерение площади со способом рационального ее вычисления.

Позднее, при решении задач с величинами площадь и периметр, дети не видят в них различия.

Для предупреждения таких ошибок, формирования у младших школьников самоконтроля при вычислении площади произвольных фигур необходимо обращать большое внимание подготовительным упражнениям, направленным на формирование представлений о конкретном смысле измерения площади. Основные этапы такой работы могут быть следующими:

1. Ознакомление учащихся с термином площадь и первичное знакомство со сравнением площадей лучше провести при выполнении практической работы по сравнению фигур, их взаимном расположении. Фигуры подбираются так, что одна из них помещается полностью внутри другой:

В математике говорят, что площадь первой фигуры больше площади второй фигуры или площадь второй фигуры меньше площади первой фигуры. Дети сравнивают еще несколько фигур. Учитель спрашивает при этом: Как узнать площадь какой фигуры больше, а какой – меньше. Приходим к выводу, что способ наложения помогает ответить на этот вопрос.

2.Затем учитель опять переходит к фронтальной работе с классом. Он предлагает сравнить на глаз, а затем путем наложения площади двух таких фигуру по отношению к которым вопрос не может быть решен тем же способом:

(С обратной стороны эти фигуры разбиты на одинаковые квадраты). Возникает проблемная ситуация. Учащиеся говорят, что путем наложения нельзя определить, площадь какой фигуры больше. Тогда учитель поворачивает фигуры обратной стороной. Учащиеся при этом обычно сами догадываются, как можно сравнить данные фигуры по площади. Кто-то из них пересчитывает число квадратов в каждой фигуре. Формулируется вывод: если фигуры нельзя сравнить по площади наложением, то можно каждую из фигур разбить на одинаковые между собой фигуры (квадраты, треугольники) и затем подсчитать, сколько их содержится в каждой фигуре. Фигура, в которой содержится большее число таких одинаковых фигур, имеет большую площадь.

3. Для закрепления можно предложить следующую практическую работу. Детям раздаем по паре одинаковых прямоугольников, которые разбиты на квадраты, разные по размерам на каждой фигуре.

Ha этом этапе учащиеся приходят к выводу: прямоугольники при наложении совпадают, но количество квадратов, На которые они разбиты, разное. Почему? Надо было разбить на одинаковые квадраты.

На втором уроке учащиеся знакомятся с единицей площади – квадратным сантиметром, учатся измерять площади фигур путем разбиения их на квадратные сантиметры с помощью линейки и карандаша, с помощью линейки или путем покрытия фигуры моделями квадратных сантиметров.

Основной метод изучения площади и способов сравнения фигур по площади – практический, а потому важнейшим условием осознанного подхода в изучении темы является точное выполнение логически связанных между собой заданий. Предлагаем один из возможных вариантов работы с младшими школьниками.

Тема урока. Ознакомление с единицами измерения площади.

Цель урока:

- осознание детьми смысла измерения площади;

- формирование умения измерять площадь фигуры в квадратных сантиметрах.

Оборудование: набор геометрических фигур, модель 1 см²

Актуализация знаний по теме

1) Учитель. Возьмите в руки 2 фигуры (показывает прямоугольник и треугольник). Какая из них занимает больше места? (прямоугольник).

У. Какая - меньше? (треугольник).

У. Как говорят в математике о площади этих фигур? (площадь треугольника меньше площади прямоугольника).

2) У. Теперь сравните следующие две фигуры по площади;

- на обратной стороне этих фигур нанесена клетка.

У. Можно ли их сравнить наложением? (нет, т.к. ни одна из них не помещается внутри другой).

У. Как можно сравнить их площади? (подсчитать количество клеток в каждой из них).

- Подготовка к объяснению нового.

У. Возьмите в руки два прямоугольника // (Учитель показывает 2 одинаковых прямоугольника с разными по размеру клетками в них).

У. Подсчитайте количество клеток в каждой из них (в прямоугольнике с мелкой клеткой их 27, с мелкой -12).

У. Почему получились разные числа? (клетки разные).

У. Что нужно сделать, чтобы получились одинаковые числа? (измерять одинаковыми клетками).

У. В каких единицах мы измеряли длину? (сантиметр, дециметр, метр).

У. А при измерении площади квадрат с какой длиной стороны можно взять чтобы у всех было одинаково? (1 см).

Учитель показывает:

Покажите на своих полосках бумаги квадрат со стороной 1 см – он называется 1 квадратный сантиметр, обозначается 1 см². Нарисуйте его в тетради, запишите (в тетради появляется 1 см².

Работа по учебнику. Рассматриваются несколько фигур разного цвета. У. Приложите модель 1 см² к зеленой полоске. Сосчитайте, сколько квадратов содержится в ней? (5 квадратов).

- как сказать по-другому? (площадь полоски равна 5 см)

- что значит, S = 5 см²? (это значит, в фигуре содержится 5 квадратных сантиметров)

Что такое 1 см²? (это квадрат со стороной 1 см).

Запишите в тетради: 5 см².

Закрепление по учебнику № 432:

У. Сколько квадратных сантиметров укладывается в

– голубой фигуре? (S голубой фигуры = 10 см²)

– розовой фигуре? (S розовой фигуры = 9 см²)

Дети измеряют фигуры в учебнике своими моделями приходят к выводу: это очень долго – каждый раз моделью измерять площадь фигуры.

У. Как это сделать быстрее? (разбить фигуру на кв.см с помощью линейки и карандаша и пересчитать количество полученных квадратов).

Практическая работа.

У. Возьмите в руки модели прямоугольника (учитель показывает модель) и на обратной стороне аккуратно карандашом и линейкой разделите его на квадраты со стороной 1 см:

как это сделать? (учитель проходит по рядам и проверяет у учеников правильность задания),

что получилось? (4x8=32 (см²)

что это значит? (в прямоугольнике содержится 32 квадрата со стороной 1 см).

Применение знаний – элементы конструирования.

У.У вас на столе по 1 треугольнику. Можно ли также вычислить его площадь?

Сравните треугольники друг у друга - какие они? (одинаковые).

У. Какую знакомую фигуру можно составить из них? (прямоугольник).

У. Чему равна площадь прямоугольника? (5x10=50 (см²))

У. А теперь найдите площадь треугольника Sтреуг.=Sпрям.: 2 = 50: 2 = 25 (см²)

У. Кто может сказать правило? (произведение сторон, образующих прямой угол разделить на 2).

Учитель показывает новую фигуру:

У. Как найти ее площадь?

Дети предлагают несколько способов:

1)Sфигуры = S1 + S2

2) Sфигуры = Sпрямоуг.+S3

3) Sфигуры = S1+S2

У. Найдите каждый своим способом. Какие получились числа? - дети сравнивают полученные числа при нахождении площади прямоугольника, получили одинаковые числа.

У. Что это означает? (площадь этой фигуры можно найти по-разному).

Вывод.

У. Площади каких фигур мы научились вычислять? (прямоугольник, прямоугольный треугольник, фигура, которую можно составить из прямоугольников).

У. Как можно сравнивать площади фигур? («на глаз», наложением, путем подсчитыванием одинаковых квадратов, на которые разбили фигуры).

Подстановка проблемы.

У. Сможем ли найти площадь любой фигуры? (учитель показывает круг, вырезанные из бумаги кленовый лист, звезду и т.д.).

Дети отвечают по-разному.

У. Это наша работа на следующий урок.

Следующий этап – знакомство с палеткой и измерение площади с помощью палетки.

Для осознанного усвоения темы полезно весь практический материал: набор всех необходимых геометрических фигур, модель 1см, палетка изготавливаются заранее детьми на уроках труда. Тогда в процессе практический работы младшие школьники учатся разводить понятия «площадь» и «периметр». Изготовленная руками учащихся палетка выступает на уроке в качестве самодельного прибора по подсчету общего количества квадратных сантиметров не расчерчивая фигуру на квадраты со стороной 1 см². Тогда и способ подсчета площади произвольной фигуры дети могут предложить сами.

Использование палетки на первых этапах ознакомления с площадью позволяет подчеркнуть общность понятия площадь для всех фигур независимо от их формы. При этом в задания по определению приближенного значению площади можно предложить и прямоугольники, длины сторон которых не содержат целое число сантиметров.

Рассмотренный подход к изучению площади исключает возможность ошибочного толкования различных способов измерения площади. Учащиеся при необходимости могут обосновать определение площади прямоугольника через произведение соответствующих чисел, опираясь на общие представления о смысле измерения площади.

Вывод правила о вычислении площади прямоугольника проводятся так, как это описано в методических пособиях и в учебнике с небольшими, но очень важными, на наш взгляд, дополнениями. Вычисляя площадь прямоугольника по правилу, необходимо подчеркивать, что, находя произведение чисел – значений длины и ширины прямоугольника, – мы фактически подсчитываем число квадратных сантиметров, содержащихся в нем. Напервых уроках, а при затруднениях и на последующих, мы считаем необходимым требовать от учащихся словесного обоснования необходимости выполнения действия умножения над соответствующими числами для определения площади прямоугольника.

 

 

Тема: Методика изучения темы «Масса»

План:

1. Порядок работы над темой.

2. Система упражнений по формированию представления о массе на основе сравнения различных значений однородных величин.

3. Последовательность упражнений, формирующих представление о массе.

4. Подготовительный урок – экскурсия в магазин, школьную столовую.

Рекомендательная литература

1. Истомина Н.Б. Знакомство с величинами // Начальная школа. – 1983. – № 1. – С. 32-35.

2. Тихоненко А.В. Формирование представлений о массе тел и емкости // Начальная школа. – 1990. – № 6.– С. 75-79.

 

Приведем эту статью

Первое представление о том, что предметы имеют массу, дети получают в своей жизненной практике еще до школы: «Не бери, это для тебя тяжело»; «Возьми, он легкий». Взяв в руки предметы, дети на основе мускульных ощущений устанавливают, какой предмет тяжелее, какой легче. Но чувственный опыт дошкольников недостаточно велик, чтобы сравнивать массу двух предметов. Так, предметы, которые имеют большой объем или занимают больше места в пространстве, всегда кажутся им большими по массе.

Для предупреждения неверных представлений возникает необходимость поиска эффективных способов измерения массы. Этапы формирования представлений об измерении массы тела аналогичны тем, которые используются при измерении длины и площади: сравнение массы предметов по ощущению (тяжелее, легче на руке), выяснение отношения «тяжелее», «легче» с помощью инструмента – чашечных весов, а затем отвешивание и развешивание груза с помощью весов и гирь (разновесов), когда уже выбрана единица измерения массы.

Знакомство с основной единицей измерения массы – килограммом – происходит в процессе выполнения практических заданий, сравнение массы предметов на основе мускульных ощущений, в результате чего учащиеся приходят к выводу о необходимости взвешивания предметов и измерения их массы к соответствующих единицах.

Предлагаем фрагмент урока учителя Г.М. Ряпикиной (школа № 10 г. Таганрога) по теме «Масса тел и ее измерение. Килограмм».

Цели: показать, что предметы можно сравнивать по массе; дать представление о массе в 1 кг; познакомить с процессом взвешивания на чашечных весах; воспитывать познавательный интерес к предмету, используя материал из истории математики.

Оборудование: две коробки (одинаковые по внешнему виду); два пакета: зеленый – массой в 990 г, синий – массой в 10 г; гири в 1 кг, 2 кг, 5 кг, 10 кг; брусок массой в 2кг; плакат с изображением разных весов; чашечные весы.

Работа над новым материалом. На столе учителя две одинаковые по форме и цвету коробки: одна пустая, а другая с песком.

Учитель проводит беседу:

– Сравните коробки.

Никаких внешних признаков различия учащиеся обнаружить не могут и делают вывод: коробки одинаковые.

– Различие между коробками есть.

Учащиеся заинтересованы. Взяв коробки, учащиеся обнаруживают, что одна коробка тяжелее другой.

– Вы сказали, что одна коробка тяжелее другой, а что можно сказать о другой коробке по отношению к первой? (Вторая коробка легче первой.)

Учитель делает заключение: «Если одна коробка тяжелее другой, то говорят так: масса одной коробки больше, чем масса другой, а масса другой коробки меньше, чем масса первой».

2. На столе – две книги, которые но массе незначительно отличаются друг от друга. Учитель вызывает к доске двух учеников и предлагает взять книги в руки и определить, какая из них тяжелее, а какая – легче.

Мнения учеников расходятся. Тогда пытаются ответить на этот вопрос другие ученики. Снова мнения учеников расходятся.

– Как же узнать, какая книга тяжелее, а какая легче? (Можно их взвесить на весах и узнать.)

– Правильно, не всегда можно определить, какой предмет легче, а какой тяжелее, если они по массе незначительно отличаются. Для этой цели лучше воспользоваться весами.

Учитель ставит на стол чашечные весы и обращает внимание учащихся на стрелки весов: они расположены строго друг против друга.

– Подумайте, что произойдет со стрелкой той чашки, на которую положим книгу? (Она опустится.)

Ученики кладут на одну чашку весов одну книгу (чашка весов опускается), затем кладут на другую чашку весов другую книгу и наблюдают, что происходит со стрелками весов. Наконец, чашки весов приходят в состояние покоя, и учащиеся выясняют, какая книга тяжелее, а какая легче.

3. На столе три предмета: гиря массой в 1 кг, зеленый пакет с солью массой 910 г и синий пакет с солью массой в 1010 v. Учитель предлагает определить, масса какого пакета легче (тяжелее). Мнения учеников снова расходятся.

– Подумайте, как решить эту задачу с помощью весов, используя гирю массой в 1 кг.

Выполняя практические действия, учащиеся устанавливают, что масса зеленого пакета меньше, чем масса гири в 1 кг, масса гири в 1 кг меньше, чем масса синего пакета. Они делают вывод, что масса зеленого пакета меньше, чем масса синего пакета.

Эта практическая работа приводит учащихся к осознанию свойства транзитивности масс (величин). Естественно, о свойстве транзитивности учитель не сообщает, но учащиеся при практических действиях его используют в неявном виде.

Для развития логического мышления и закрепления только что выявленного свойства масс учитель предлагает следующие задачи:

Задача 1. Известно, что предмет А тяжелее предмета В, предмет? В тяжелее предмета С. Что можно сказать о массе предметов А и С, не взвешивая их? Какой из этих предметов самый тяжелый?

Учащиеся, рассуждая, устанавливают, что предмет А тяжелее предмета С: значит, самый тяжелый предмет А, а самый легкий – предмет С.

Задача 2. Известно, что предмет А легче предмета В, а предмет С имеет такую же массу, как и предмет В. Не производя взвешивания, какой вывод можно сделать о массе предметов А и С? Какой из них тяжелее?

Учащиеся устанавливают, что если предмет А легче, чем В, а предмет В одинаков по массе с предметом С, то предмет А легче, чем С, значит, предмет С тяжелее, чем предмет А.

4. На левую чашку весов учитель кладет брусок массой в 2 кг (масса не сообщается), а на правую – гирю массой в 1 кг. Учащиеся наблюдают за весами и устанавливают, что масса бруска больше, чем масса гири в 1 кг. Тогда учитель предлагает на правую чашку весов поставить еще гирю массой в 1 кг. Чашки уравновешиваются.

– Что можно сказать о массе бруска? (Его масса – 2 кг.)

Учитель замечает, что вместо двух гирь массой в 1 кг можно воспользоваться гирей массой в 2 кг (ставит гирю массой в 2 кг на правую чашку весов, а гири массой по 1 кг снимает).

Эти практические действия помогают учащимся осознать, что массы (величины) можно складывать: 1 кг + 1 кг = 2 кг. Таким образом, учащиеся знакомятся еще с одним свойством величин.

Далее учитель сообщает, что в практической жизни используют гири массой в 5 кг, 10 кг (выставляет эти гири на стол). Учащиеся пытаются их поднять. Учитель предостерегает: «Не трогайте! Они тяжелые». Он сам сначала поднимает одну гирю, затем другую.

Для расширения представлений о килограмме и для совершенствования вычислительных навыков учитель использует наглядные модели весов и разновесов, сделанные из картона, и картинки с изображением различных предметов, предлагая следующие задания:

1) На одной чашке весов – 2 буханки хлеба, а на другой – 2 гири массой в 1 кг каждая. Если чашки весов находятся в положении равновесия, то чему равна масса двух буханок хлеба?

2) На одной чашке весов – помидоры, на другой – 2 гири в 1 кг и 2 кг. Определите массу помидоров, если чашки весов находятся в равновесии.

3) На одной чашке весов – картофель и гиря массой в 2 кг, на другой – гиря массой в 5 кг. Чашки весов находятся в равновесии. Какова масса картофеля?

При выполнении этих упражнений рассматриваются ситуации, часто встречающиеся в повседневной жизни и вызывающие поэтому интерес. Кроме того, они способствуют формированию умения определять массу тела и получать образное представление о массе в 1 кг, 2 кг и 5 кг.

5. На следующем этапе урока с целью воспитания познавательного интереса к математике учитель делает краткое сообщение:

– Какой народ и когда изобрел весы, мы не знаем. Видимо, это было сделано многими народами независимо друг от друга. До наших дней дошло много изображений весов. Одними из первых весов, относящимися ко второму тысячелетию до новой эры были рычажные весы. На Руси, например, пользовались весами двух видов: безменом и чашечными, которые в те времена назывались скалвой. Эти весы были более точными, и немецкие купцы, торговавшие с Новгородом, взвешивали все товары только на скалве. И в наши дни человека, готового на ссору из-за мелких расчетов, называют сквалыжником. (Учитель вывешивает плакат, на котором изображены различные виды весов – от древнейших до современных.)

Древнейшими единицами массы на Руси были гривна, фунт и пуд. У других народов были свои единицы массы.

Более 200 лет назад ученые Франции предложили изготовить куб, сторона которого равнялась 10 см (учитель показывает), наполнили его дистиллированной водой и взвесили при температуре 4°С. Массу этой воды стали считать равной 1 кг. Затем из платины изготовили цилиндрической формы гирю массой в 1 кг, которая стала эталоном – образцом. Позднее из металла изготовили гири массой в 1 кг; 2 кг, 5 кг, 10 кг и др.

Продолжая урок, учитель выясняет, массу какихпредметов и продуктов можно измерить гирей в 1 кг, 2 кг, 5 кг, 10 кг.

Учащиеся устанавливают (на основе жизненного опыта), что если брать небольшое количество продуктов, то их можно измерить гирей массой в 1 кг, 2 кг. А лук, картофель, например, заготавливая на зиму, удобнее взвешивать гирей в 10 кг.

Учитель делает вывод: Масса измеряется в килограммах; 1 кг – это единица измерения массы (записывает на доске, а учащиеся в тетрадях).

6. Практическая работа по определению массы предметов и продуктов: пачки сахара, пакета картофеля, портфеля с ученическими принадлежностями. В процессе практической деятельности дети учатся уравновешивать чашки весов. Далее, совершенствуя вычислительные навыки, учитель показывает плакат с изображением весов. В прорезь на левую чашку весов вставляет карточки с записями 3 кг, 5 кг, 3 кг и 5 кг, и спрашивает: «Какие гири следует поставить на правую чашку весов, чтобы чашки уравновесить?» (1 кг и 2 кг; 2 кг, 2 кг и 1 кг; 5 кг, 1 кг и 2 кг). Для закрепления материала учащиеся выполняют задания:

1. Масса пакета 2 кг, а масса портфеля 5 кг. Сравните массы пакета и портфеля. Запишите результат сравнения. (Масса пакета меньше, чем масса портфеля: 2 кг < 5 кг.)

2. Масса сумки с продуктами 2 кг, масса пакета с мукой 2 кг. Сравните их массы. (Их массы равны: 2 кг = 2 кг).

После ознакомления с единицей измерения массы – килограммом учащиеся знакомятся с единицей емкости – литром.

Каждый урок – это определенная система заданий, которая ведет ученика к овладению теми или иными понятиями. От того, какие задания подбирает учитель для данного урока, в какой последовательности их выстраивает, существенно зависит достижение цели урока, а также степень активности и самостоятельности учащихся в процессе познания. Учебные задания конкретизируют методы обучения, используемые учителем на уроке, определяют структуру и внутреннюю логику урока, характер познавательной деятельности учащихся. Важно остановиться на том, какими принципами должен руководствоваться учитель, чтобы в процессе выполнения различных заданий урока учащиеся не только владели суммой определенных знаний, умений и навыков, но и продвигались в своем развитии.

Прежде всего необходимо, чтобы процесс выполнения заданий не сводился только к воспроизведению полученных знаний, а дополнялся наблюдениями, анализом, сравнением. Последовательность заданий на уроке должна быть выстроена таким образом, чтобы предыдущие задания подготавливали ученика к выполнению следующего. Это обеспечивается органическим включением ранее усвоенных знаний в процесс овладения новыми знаниями. Покажем, как реализуются эти положения в практике работы школы. Для этой цели приведем фрагмент урока по теме «Литр» (подход Д.Б. Эльконина-В.В. Давыдова).

Цель: познакомить со способом установления равенства и неравенства объектов; с литром как единицей емкости; с процессом измерения емкости с помощью литра.

1. Работа над новым материалом.

Учитель предлагает из нескольких сосудов, стоящих на столе, подобрать такой, в который поместится столько же воды, сколько ее в сосуде, который учитель демонстрирует в качестве образца. Задача решается с учетом интересного для детей сказочного сюжета:

Как-то раз Винни-Пух пришел в гости к Кролику. Как настоящий гостеприимный хозяин, Кролик решил угостить своего друга. Поставил пирог на стол и пошел за чашками для компота; открыл дверцу буфета и призадумался: у него не оказалось одинаковых чашек. Винни может обидеться, если у него будет чашка меньше. Как же быть? Давайте поможет Кролику выбрать чашку!

Учитель ставит на стол различные чашки: чашку, из которой пьет Кролик (чашка-образец), и ряд других, различной емкости и формы.

– Какие предложения у вас, ребята? Можете подойти к столу посмотреть чашки поближе, а вместо компота используйте воду.

Для более прочного овладения определенными действиями учитель преднамеренно направляет учащихся на неправильный вариант решения:

Давайте возьмем эту чашку. Смотрите, какая она маленькая и красивая. Винни она обязательно понравится. (Нет, мы не можем ее взять: в нее помещается меньше воды, чем в чашке Кролика.)

– Почему? Как ты это узнал?

Один из учеников выходит к доске, начинает оперировать предметами, стоящими на столе, сопровождая свои действия словами:

– Нальем воду в чашку Кролика, а затем перельем в эту чашку. Вода помещается не вся, значит, эта чашка меньше, чем чашка Кролика.

Учитель предлагает еще ряд вариантов. В ходе обсуждения практических действий находится нужная чашка.

Показывая найденную чашку и чашку Кролика, учитель говорит, что такие чашки называются одинаковыми по емкости: они вмещают одинаковое количество жидкости. В ходе практической работы устанавливается, что среди сосудов, стоящих на столе, нет больше одинаковых по емкости (ни одна из чашек не вмещает столько же воды, сколько чашка Кролика, следовательно, их емкость различна).

– Итак, мы помогли Кролику найти такую же по емкости чашку, как у него. Поставил он чашки на стол, разлил компот, и тут кто-то постучал в дверь. Это был Пятачок. Кролик пригласил его к столу и призадумался: ведь у него только две одинаковые по емкости чашки. Как же быть? Кролику не хотелось обидеть Пятачка: нужно, чтобы компота досталось поровну всем друзьям.

В процессе обсуждения учащиеся под руководством учителя приходят к выводу о том, что можно взять другую чашку, но налить в нее