Пример решения задачи № 1. (Выписывается текст задания – см
(Выписывается текст задания – см. п. 8.1). Решение: рама (рис. 8.4, а) имеет четыре участка. На каждом участке в произвольном поперечном сечении указываем пространственную систему координат Oxyz: оси Ох и Оу совмещаем с главными центральными осями поперечного сечения, а ось Oz – с осью стержня. (Систему Oxyz называют скользящей: при перемещении ее вдоль оси стержня с одного участка на другой (с поворотом в узловой точке) оси системы Oxyz каждого участка могут быть совмещены с соответствующими им осями соседнего участка). Положение произвольного сечения каждого участка задаем координатой zi, отсчитываемой от начала участка со стороны свободного (незаделанного) конца рамы.
  
 
Рисунок 8.4 – Расчетная схема рамы и эпюры Мх, Му, Мк Составляем аналитические выражения изгибающих и крутящих моментов для каждого участка: Участок I (CD) Участок II (BC)
Участок III (BK) Участок IV (AB)
(Правило знаков для изгибающих моментов то же, что при построении эпюр для балок. При этом взор должен быть направлен к началу координат со стороны оси х, если записывается аналитическое выражение для Вычисляя значения моментов по концам каждого стержня, строим эпюры Участки I, III находятся в условиях прямого изгиба. В их сечениях возникает по одному изгибающему моменту:
Рисунок 8.5 – Схемы к анализу напряженных состояний в опасных точках
Определяем необходимые диаметры сечений по условиям проч-ности:
откуда
Принимаем: Тогда
Имеем недонапряжение:
Аналогично
Перенапряжение:
В опасном сечении участка II возникают изгибающий Эпюры распределения нормальных и касательных напряжений показаны на рис. 8.5, в. Опасными точками являются точки А и В, так как в них и нормальные и касательные напряжения достигают наибольших значений:
Эквивалентное напряжение по гипотезе наибольших касательных напряжений (третья гипотеза прочности)
Определяем размер сечения по условию прочности:
Принимаем а = 63 мм. Тогда
Перенапряжение:
При подборе не квадратного, а, например, кольцевого сечения последовательность расчета будет иной: – эквивалентный момент по третьей гипотезе прочности:
– осевой момент сопротивления кольцевого сечения (при
Принимаем: D = 75 мм, d = 38 мм, k = 38 / 75 = 0,507. Тогда
Недонапряжение:
Опасным сечением АВ (IV) является сечение заделки, в котором возникают моменты:
Эпюры распределения нормальных и касательных напряжений представлены на рис. 8.5, г. Влияние поперечных сил при подборе размеров поперечного сечения учитывать не будем. Наиболее напряжённой (опасной) точкой сечения может оказаться одна из точек: А, В, С. Определим расчетные напряжения в этих точках. В точке А напряженное состояние – линейное (одноосное):
В точке В напряженное состояние – плоское (частный случай, характерный для изгиба с кручением). При этом
В точке С напряженное состояние – плоское, аналогичное напряженному состоянию точки В:
Сопоставление найденных значений расчетных напряжений показывает, что опасной точкой сечения является точка В. По условию прочности
имеем:
Принимаем: h = 53 мм; b = 2 h = 106 мм. Проверим прочность на участке АВ (IV) с учетом влияния поперечных сил:
Для найденных размеров сечения
Для точки А
Для точки В
Так как направления
Эквивалентное напряжение в точке В (по третьей гипотезе прочности):
Перенапряжение составляет:
В точке С касательное напряжение от поперечной силы
где
Нормальное напряжение в точке
Эквивалентное напряжение:
Проверочный расчет подтверждает обоснованность пренебрежения влиянием поперечных сил при подборе размеров поперечного сечения в рассматриваемом случае. Участок АВ, имеющий прямоугольное поперечное сечение, находится в условиях косого изгиба и кручения. Определим положение нейтральной оси опасного сечения при косом изгибе. Предварительно, выполнив графическое построение (рис. 8.6), находим положение силовой линии сечения. Из этого построения следует, что
откуда Определяем угол (
Мх = 1,44 кНм; Му = 8 кНм; a = 79,8о; j = 54,3о
Рисунок 8.6 – Определение нейтральной оси опасного сечения участка АВ
Нейтральная ось (см. рис. 8.6) делит поперечное сечение на две зоны, отличающиеся знаком нормальных напряжений (зоны растяжения и сжатия продольных волокон бруса).
|















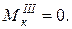

 , и со стороны оси у, если – для
, и со стороны оси у, если – для  Крутящий момент Мк считаем положительным, если при взгляде на сечение со стороны внешней нормали он направлен против хода часовой стрелки).
Крутящий момент Мк считаем положительным, если при взгляде на сечение со стороны внешней нормали он направлен против хода часовой стрелки). ,
,  (см. рис. 8.4, б, в, г).
(см. рис. 8.4, б, в, г).

 ;
;  ,
,
 ;
;
 .
. мм,
мм, 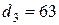 мм.
мм. ;
;
 .
.


 кНм) и крутящий (
кНм) и крутящий (




 .
.




 .
. ;
; .
.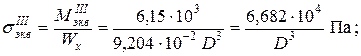
 .
.

 .
.




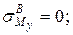



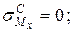



 , или
, или 

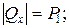









 и
и  совпадают, то полное касательное напряжение в точке В равно:
совпадают, то полное касательное напряжение в точке В равно:

 .
. направлено навстречу напряжению
направлено навстречу напряжению  , поэтому результирующее напряжение
, поэтому результирующее напряжение 

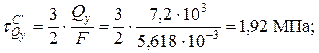

 :
:
 .
.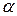 < 0, и поэтому
< 0, и поэтому ,
, .
. ) отклонения нейтральной оси сечения от главной центральной оси х:
) отклонения нейтральной оси сечения от главной центральной оси х:
 .
.



