Методические указания по выполнению задания
В задаче № 1 требуется выполнить проектировочный расчет плоской рамы, элементы которой находятся в разных условиях нагружения и имеют различную форму сечения. Чтобы определить вид нагружения каждого участка рамы, необходимо, пользуясь методом сечений, построить эпюры внутренних силовых факторов. С учетом того, что касательные напряжения, связанные с изгибом, в сечениях сплошной формы обычно невелики, эпюры Если участок имеет круглое или кольцевое сечение и в его сечениях согласно построенным эпюрам возникают изгибающие и крутящие моменты, следует определить сечение, в котором эти моменты наибольшие. Это сечение называют опасным, так как в нем имеются две точки, также называемые опасными, в которых расчетные напряжения достигают наибольших значений в сравнении с любыми другими точками участка. Опасные точки находятся на концах диаметра, перпендикулярного к вектору результирующего изгибающего момента в сечении:
Условие прочности для пластичных материалов согласно гипотезе наибольших касательных напряжений (третья гипотеза прочности) и гипотезе удельной потенциальной энергии формоизменения (четвертая гипотеза прочности), устанавливающим критерии пластичности, в случае круглого или кольцевого сечения записывается в виде:
где
где Моменты В случае проектировочного расчета необходимые размеры сечения определяются по условию прочности (8.2):
Если участок рамы, находящийся в условиях изгиба с кручением, имеет некруглое, в частности прямоугольное сечение, то понятие "эквивалентный (расчетный, приведенный) момент" неприменимо. Поскольку наибольшие значения напряжений от кручения и изгиба могут возникать в разных точках исследуемого сечения, опасными могут быть точки с наибольшими нормальными напряжениями, точки с наибольшими касательными напряжениями или точки, в которых нормальные и касательные напряжения имеют промежуточные значения. Указать опасную точку опасного сечения часто можно, лишь вычислив значения эквивалентных напряжений в нескольких (предположительно опасных) точках и сравнив полученные результаты. Эквивалентные напряжения при изгибе с кручением в случае некруглых сечений вычисляют: – по третьей гипотезе прочности:
– по четвертой гипотезе прочности:
При этом нормальные напряжения s следует определять по формуле
где изгибающие моменты Мх, Му и координаты точки (х, у), в которой определяются напряжения, берутся по абсолютной величине, а знак напряжений устанавливается по правилу: при растяжении соответствующего волокна s > 0, а при сжатии – s < 0, что легко определить по рисунку сечения и направлению изгибающих моментов Мх и Му в этом сечении. Наибольшие значения касательных напряжений в прямоугольном сечении возникают в крайних точках сечения, расположенных посередине длинных сторон:
где Wk – момент сопротивления сечения при кручении:
где b – длина короткой стороны; b – коэффициент, выбираемый из справочной таблицы 8.3. Касательные напряжения, возникающие посередине коротких сторон сечения, имеют меньшие значения:
где g – коэффициент, меньший единицы. Значения коэффициентов b и g зависят от отношения длин сторон прямоугольника (табл. 8.3) [1].
Таблица 8.3 – Значения коэффициентов a, b, g
Коэффициент a используется при вычислении геометрической характеристики крутильной жесткости
где G – модуль упругости материала при сдвиге;
В некоторых случаях при определении касательных напряжений По условию прочности sэкв < [ s ], где sэкв определяется по (8.7) или (8.8), нетрудно определить размеры поперечного сечения стержня, так как соотношение этих размеров h / b задано. Построение нейтральной оси поперечного сечения прямоугольной формы (согласно требованию п. 4 задачи № 1) нетрудно выполнить, вычислив угол наклона
где Угол При Формула (8.15) соответствует косому изгибу, то есть изгибу, при котором в сечении возникают два изгибающих момента Мх и Му, а нормальная сила N отсутствует. Положение силовой линии, то есть следа плоскости действия результирующего изгибающего момента М в сечении, определяется по направлению перпендикуляра, проведенного через центр тяжести сечения к направлению вектора – мо-
|

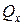 и
и  строить необязательно, ограничившись построением эпюр крутящих и изгибающих моментов.
строить необязательно, ограничившись построением эпюр крутящих и изгибающих моментов. (8.1)
(8.1) (8.2)
(8.2) – эквивалентное (расчетное) напряжение опасной точки по соответствующей гипотезе прочности; Wx – осевой момент сопротивления сечения, вычисляемый для круглого (диаметром D) и кольцевого сечений соответственно по формулам (d – внутренний диаметр кольца, D – наружный):
– эквивалентное (расчетное) напряжение опасной точки по соответствующей гипотезе прочности; Wx – осевой момент сопротивления сечения, вычисляемый для круглого (диаметром D) и кольцевого сечений соответственно по формулам (d – внутренний диаметр кольца, D – наружный):

 (8.3)
(8.3)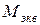 – эквивалентный (расчетный) момент по третьей или четвертой гипотезе прочности соответственно:
– эквивалентный (расчетный) момент по третьей или четвертой гипотезе прочности соответственно: (8.4)
(8.4) (8.5)
(8.5) и
и  – изгибающие моменты в сечении;
– изгибающие моменты в сечении;  – крутящий момент в этом же сечении.
– крутящий момент в этом же сечении. (8.6)
(8.6)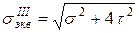 ; (8.7)
; (8.7) . (8.8)
. (8.8) , (8.9)
, (8.9) , (8.10)
, (8.10) , (8.11)
, (8.11) , (8.12)
, (8.12)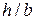
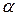
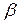
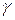
 , необходимой для вычисления угла закручивания j стержня длиной ℓ;:
, необходимой для вычисления угла закручивания j стержня длиной ℓ;: (8.13)
(8.13)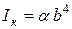 . (8.14)
. (8.14) следует учитывать и напряжения
следует учитывать и напряжения 
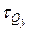 ).
). этой оси к главной центральной оси х сечения:
этой оси к главной центральной оси х сечения: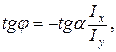 (8.15)
(8.15)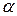 – угол между силовой линией в сечении и главной центральной осью y сечения.
– угол между силовой линией в сечении и главной центральной осью y сечения.


