Методические указания по выполнению задания. Практические расчеты сжатых стержней на устойчивость проводятся по условию
Практические расчеты сжатых стержней на устойчивость проводятся по условию
где Р – осевая нагрузка; Произведение Значения коэффициента Как следует из (7.1), площадь сечения стержня должна удовлетворять условию
Коэффициент
где
Предполагается, что опорные закрепления стержня таковы, что приведенная длина в обеих главных плоскостях одинакова. Поэтому потеря устойчивости прямолинейной формы равновесия стержня возможна в плоскости наименьшей жесткости. Следовательно, для определения гибкости необходимо вычислить наименьший момент инерции сечения Чтобы найти эти величины, нужны численные значения размеров сечения, которые могут быть получены лишь после решения неравенства (7.2). Последнее же содержит два неизвестных: F и Задачу определения размеров сечения обычно решают методом проб (последовательных приближений). В первом приближении можно задаться значением коэффициента Табличное значение коэффициента Расчет можно считать законченным, если действующее напряжение По завершении расчета на устойчивость следует проверить прочность стержня по ослабленному местным вырезом сечению. Так как центр тяжести ослабленного сечения смещен относительно линии действия сжимающих сил, то имеет место внецентренное сжатие. Необходимо найти положение центра тяжести, определить внутренние силовые факторы в этом сечении и вычислить максимальное напряжение, которое не должно превышать [ s ]. Если это условие не выполнено, следует увеличить номер профиля и повторить расчет на прочность, добившись соблюдения условия Примечание: в связи с тем, что строительные конструкции рассчитываются в настоящее время по методу предельных состояний, более прогрессивному, нежели метод допускаемых напряжений, студентам строительных специальностей при выполнении данного задания следует пользоваться методом предельных состояний. Условие устойчивости (7.1) при этом записывают в виде [4, 5]
где Для подбора площади сечения (
Последовательность расчета та же, что по методу допускаемых напряжений. При этом расчет следует считать законченным, если расчетное напряжение Ослабленное сечение проверяется по условию прочности:
аналогично методу допускаемых напряжений.
|

 (7.1)
(7.1) – площадь поперечного сечения стержня без учета местных ослаблений; [ s ] – основное допускаемое напряжение, принимаемое в расчетах на прочность при сжатии;
– площадь поперечного сечения стержня без учета местных ослаблений; [ s ] – основное допускаемое напряжение, принимаемое в расчетах на прочность при сжатии;  – коэффициент снижения основного допускаемого напряжения (коэффициент продольного изгиба).
– коэффициент снижения основного допускаемого напряжения (коэффициент продольного изгиба). есть допускаемое напряжение в расчетах на устойчивость.
есть допускаемое напряжение в расчетах на устойчивость. ) стержня. Таблицы значений коэффициента
) стержня. Таблицы значений коэффициента  (7.2)
(7.2) (7.3)
(7.3) – длина стержня;
– длина стержня;  – приведенная длина;
– приведенная длина;  – коэффициент приведения длины;
– коэффициент приведения длины;  – минимальный радиус инерции сечения стержня:
– минимальный радиус инерции сечения стержня: (7.4)
(7.4) и соответствующий радиус
и соответствующий радиус 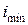 инерции.
инерции. .
. , после чего по (7.2) легко найти F. Так как в данном задании одна из частей сечения известна, то площадь второй части по найденному значению F нетрудно определить. Вслед за этим решается задача определения главных центральных осей сечения, вычисляются значения
, после чего по (7.2) легко найти F. Так как в данном задании одна из частей сечения известна, то площадь второй части по найденному значению F нетрудно определить. Вслед за этим решается задача определения главных центральных осей сечения, вычисляются значения 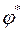 для заданного материала стойки. При этом пользуются формулой линейной интерполяции, если полученного значения l в таблице нет.
для заданного материала стойки. При этом пользуются формулой линейной интерполяции, если полученного значения l в таблице нет. обычно заметно отличается от принятого (
обычно заметно отличается от принятого ( , либо принимая новые размеры сечения непосредственно. Как правило, приходится делать несколько попыток.
, либо принимая новые размеры сечения непосредственно. Как правило, приходится делать несколько попыток. отличается от допускаемого
отличается от допускаемого 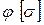 не более чем на 3-5 %. Если это не удается по причине отсутствия в таблицах стандарта подходящего по площади номера профиля, то можно допустить недогрузку, превышающую 5 %, но при условии, что уменьшение номера профиля приведет к перенапряжению, превышающему 5 %, а это недопустимо.
не более чем на 3-5 %. Если это не удается по причине отсутствия в таблицах стандарта подходящего по площади номера профиля, то можно допустить недогрузку, превышающую 5 %, но при условии, что уменьшение номера профиля приведет к перенапряжению, превышающему 5 %, а это недопустимо. .
.
 – расчетное напряжение; R – расчетное сопротивление
– расчетное напряжение; R – расчетное сопротивление 
 отличается от расчетного сопротивления R не более чем на 3-5 %.
отличается от расчетного сопротивления R не более чем на 3-5 %. ,
,


