Пример решения задачи № 2. Вычерчиваем расчетную схему рамы в масштабе, выбрав исходные данные из табл
Вычерчиваем расчетную схему рамы в масштабе, выбрав исходные данные из табл. 6.2 (рис. 6.8, а). (Выписывается текст задания – см. п. 6.1). Решение: определяем реакции опор из уравнений равновесия статики:
Проверка по уравнению Найденные значения реакций опор указываем на чертеже расчетной схемы рамы (рис. 6.8, а). Разбиваем раму на участки и составляем аналитические выражения внутренних силовых факторов: Участок I Участок II Участок III Участок IV (
Пользуясь этими выражениями, строим эпюры Для определения линейного перемещения сечения В прикладываем в т. В единичную силу в направлении искомого перемещения, находим реакции опор и, пользуясь методом сечений, строим эпюру изгибающих моментов («единичную» эпюру – см. рис. 6.8, д). Перемножив «грузовую» и «единичную» эпюры изгибающих моментов по способу Верещагина, получим перемещение т. В (см.
а – расчетная схема рамы, б, в, г – эпюры внутренних силовых факторов от заданной нагрузки, д, е – «единичные» эпюры. Рисунок 6.8 – Схемы к расчету статически определимой рамы
Для определения угла поворота узла С нагружаем раму в этом узле единичным моментом, находим реакции опор и строим эпюру изгибающих моментов (см. рис. 6.8, е). Перемножая «грузовую» и «единичную» эпюры изгибающих моментов (Мх и М 2), находим:
Направления перемещений совпали с направлениями единичных силовых факторов, так как полученные результаты положительны. Ответ на второй вопрос задания получим, решив следующее уравнение:
где левая часть есть выражение нового значения перемещения т. В, то есть с учетом действия силы X; Определим
Тогда при
Сила X должна быть приложена в направлении, противоположном направлению единичной силы. При этом новое значение пере-мещения т. В
Направление перемещения в т. В сохраняется.
|

 :
:  ;
;  .
. :
:  ;
; 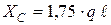 .
. :
:  ;
;  .
. : – XA + Xc = 0; XA = Xc.
: – XA + Xc = 0; XA = Xc. ) (
) ( ) (
) ( ) (
) ( )
)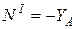 ;
; 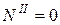 ;
; 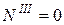 ;
;  ;
; ;
;  ;
;  ;
; 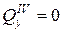 ;
; .
.  .
.  .
. 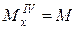 .
.
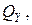



 .
. ,
, – перемещение в направлении единичной силы, приложенной в точке В (см. рис. 6.8, д), вызванное этой силой.
– перемещение в направлении единичной силы, приложенной в точке В (см. рис. 6.8, д), вызванное этой силой. саму на себя:
саму на себя: .
. находим:
находим: .
.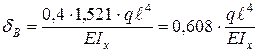 .
.


