Методические указания по решению задач
Первые две задачи задания № 6 являются статически определимыми, поскольку для нахождения реакций опорных связей достаточно уравнений равновесия статики, а дополнительных внутренних связей заданные системы не содержат. К решению этих задач следует приступить после изучения графо-аналитического способа вычисления интеграла Мора, предложенного в 1925 г. студентом Московского института инженеров железнодорожного транспорта А.К. Верещагиным и называемого поэтому правилом (или способом) Верещагина. Необходимый материал содержится, например, в учебниках [1, с. 203 – 208; 2, c. 241 – 243]. Следует также внимательно ознакомиться с примерами решения задач № 1 и 2, приведенными в настоящем пособии, где способ Верещагина подробно объясняется. В задачах № 3 и 4 расчету подлежат статически неопределимые системы - рама и балка. Расчет рамы (задача № 3) требуется выполнить, применив для раскрытия статической неопределимости метод сил, предварительно изучив соответствующий материал по конспекту лекций и учебнику [1, с. 217 – 230; 248 – 250], а также ознакомившись с примерами расчета, приведенными в данном пособии. Расчет стержневой системы с использованием метода сил производится в следующей последовательности. Прежде всего определяют степень статической неопределимости системы как разность между числом неизвестных усилий и числом независимых уравнений статики, которые могут быть составлены для заданной системы. Иначе, степень статической неопределимости равна числу дополнительных ("лишних") связей, то есть числу связей, наложенных на систему сверх необходимого числа связей, при котором уже достигается ее кинематическая неизменяемость (неподвижность). Все статически определимые системы имеют необходимое число связей. Затем выбирают основную систему, под которой понимается статически определимая система, получаемая из заданной путем отбрасывания дополнительных ("лишних") связей. Оставшиеся связи должны обеспечить кинематическую неизменяемость системы. На это обстоятельство следует обратить внимание. Если кинематическая неизменяемость системы не обеспечена, то при ее нагружении равновесие, как правило, невозможно. Например, нельзя выбирать основную систему так, чтобы направления оставшихся опорных стерженьков пересекались в одной точке. Она может быть выбрана в различных вариантах. Предпочтение следует отдавать такой основной системе, при которой последующий расчет будет проще. Например, если заданная система имеет одну из опор в виде заделки, то при выборе основной системы заделку, как правило, сохраняют. Это облегчает задачу построения эпюр внутренних силовых факторов. После выбора основной системы записывают канонические уравнения метода сил [1, с. 226]. Их число равно степени статической неопределимости. Для нахождения коэффициентов и свободных членов канонических уравнений удобно применять способ Верещагина, так как рама состоит из прямолинейных участков. Решением системы составленных канонических уравнений определяют все неизвестные реакции дополнительных связей. Раскрытие статической неопределимости на этом заканчивается. Остальные реакции связей при необходимости находят из уравнений статики. Дальнейший расчет проводится так же, как и в статически определимой системе. Построение эпюр внутренних силовых факторов выполняется в основной системе при учете действия найденных значений реакций дополнительных связей. Построенные эпюры являются окончательными для заданной системы. Необходимо проверить верность построенных эпюр по тем же правилам, которые используются в случае статически определимых систем, а кроме того, выполнить деформационную проверку. Она состоит в вычислении перемещения точки системы, расположенной на одной из опор, путем перемножения по способу Верещагина окончательной эпюры изгибающих моментов с соответствующей "единичной" эпюрой. Последнюю строят в основной системе от единичной силы, приложенной в направлении определяемого перемещения. Причем основная система может выбираться в другом варианте, не использованном в расчете. При отсутствии ошибок в расчете результат перемножения эпюр будет равен нулю. По такой же схеме производится определение неизвестных перемещений точек заданной системы или углов поворота сечений. Примеры расчета приведены в настоящем пособии (см. примеры решения задач № 3 и 4). Расчет неразрезной балки (задача № 4) также может быть выполнен методом сил. Степень статической неопределимости неразрезной балки с шарнирными опорами по концам равна числу промежуточных опор. При наличии заделки одного из концевых сечений степень статической неопределимости равна числу дополнительных (шарнирных) опор. Если имеется еще одна заделка (другого концевого сечения), то степень статической неопределимости увеличивается на две единицы, а не на три, так как во избежание возникновения температурных (осевых) напряжений опора должна допускать свободное осевое перемещение концевого сечения. В качестве основной системы может быть выбрана статически определимая балка, получаемая из заданной путем отбрасывания дополнительных опорных связей. Однако при таком выборе основной системы в каждое из канонических уравнений метода сил входят все неизвестные реакции дополнительных связей. В расчетной практике получил распространение другой способ выбора основной системы. Ее получают разрезанием балки над промежуточными опорами, то есть получают совокупность однопролетных балок, каждая из которых может деформироваться независимо от остальных. Основными неизвестными в этом случае являются изгибающие моменты в сечениях над промежуточными опорами (опорные моменты). Условия эквивалентности разрезанной над промежуточными опорами балки и заданной неразрезной балки выражаются в виде уравнений, в каждое из которых входит не более трех неизвестных опорных моментов. Это является достоинством такого выбора основной системы, так как при высокой степени статической неопределимости существенно упрощается решение системы уравнений, содержащих основные неизвестные. Получаемые уравнения называют уравнениями трех моментов. Известны различные формы записи этих уравнений, отличающиеся формой представления правой части. Наиболее распространенная из них имеет вид:
где Если построенные эпюры изгибающих моментов сложные, то при вычислении статических моментов площадей эпюр ( В этом случае
где k и m – соответственно число простых составляющих площадей эпюр на левом и правом пролетах, примыкающих к эпюре n. Следует иметь в виду, что значения площадей эпюр учитываются со знаком: берется знак (+), если изгибающие моменты на участке положительны, и (–), если они отрицательны. Более предпочтительной является следующая форма уравнения трех моментов [3]:
где Для данной балки составляют столько уравнений трех моментов, сколько она имеет промежуточных опор. Шарнирные опоры балки предварительно нумеруют слева направо, начиная с нуля. Балка, имеющая заделку, сводится к балке на шарнирных опорах путем замены заделки пролетом нулевой длины, шарнирные опоры которого получают соответствующие номера. Если балка имеет консоль, то нагрузку, приложенную к консоли, методами статики приводят к крайней шарнирной опоре. В результате приведения получают силу, приложенную в опорном сечении, и момент. Данный момент удобно считать известным опорным моментом и учитывать в левой части соответствующего уравнения трех моментов. В таком случае его не следует включать в нагрузку пролета, к которому примыкает консоль, то есть эпюра изгибающих моментов строится от нагрузки на пролете без учета этого момента. Полагая в уравнении трех моментов n = 1, 2,..., получают необходимое число уравнений. В результате решения системы уравнений трех моментов определяют неизвестные изгибающие моменты в сечениях балки над промежуточными опорами. На этом заканчивается раскрытие статической неопределимости. Затем переходят к построению окончательных эпюр поперечных сил и изгибающих моментов. Каждый пролет балки следует рассмотреть отдельно, определить реакции опор от нагрузки с учетом найденных опорных моментов и, пользуясь методом сечений, составить аналитические выражения для Qу и Мх, по которым и построить Деформационная проверка правильности расчета, а также определение линейных и угловых перемещений в балке согласно заданию могут осуществляться с использованием способа Верещагина, аналогично тому, как это делается в расчетах рам. В некоторых случаях может оказаться более удобным применение универсального уравнения упругой линии, в особенности при выполнении деформационной проверки. Примечания (для студентов строительных специальностей): 1. При выполнении задания следует иметь в виду, что в настоящее время все конструкции промышленных и гражданских сооружений, мостов и других объектов в строительстве рассчитываются по методу предельных состояний. Поэтому, решая задачи № 1 и 4, условия прочности балки по нормальным и касательным напряжениям необходимо записывать в виде:
где R – расчетное сопротивление материала по пределу текучести; При этом нагрузка является расчетной. Принять: R = 240 МПа; Rc = 140 МПа. 2. Эпюры изгибающих моментов следует строить со стороны растянутых волокон, откладывая ординаты на эпюрах по правилу: (–) – вверх, (+) – вниз. В остальном руководствоваться вышеизложенным, а также приведенным ниже примером выполнения задания для студентов машиностроительных специальностей.
|

 (6.1)
(6.1)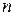 – номер промежуточной опоры балки;
– номер промежуточной опоры балки;  – площадь эпюры изгибающих моментов, построенной в основной системе от нагрузки
– площадь эпюры изгибающих моментов, построенной в основной системе от нагрузки  – то же для пролета (n + 1), то есть пролета, примыкающего к опоре n справа;
– то же для пролета (n + 1), то есть пролета, примыкающего к опоре n справа;  и
и  ) приходится пользоваться способом расслаивания эпюр на простые составляющие части, для которых легко найти площадь и положение центра тяжести.
) приходится пользоваться способом расслаивания эпюр на простые составляющие части, для которых легко найти площадь и положение центра тяжести.
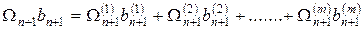 ,
,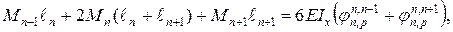 (6.2)
(6.2) и
и  – соответственно углы поворота сечения n в основной системе от действия нагрузки на смежных пролетах, примыкающих к опоре n. Здесь верхние индексы указывают направления отсчета координат точек приложения нагрузки вдоль соответствующего пролета при вычислениях этих углов. С техникой определения величин
– соответственно углы поворота сечения n в основной системе от действия нагрузки на смежных пролетах, примыкающих к опоре n. Здесь верхние индексы указывают направления отсчета координат точек приложения нагрузки вдоль соответствующего пролета при вычислениях этих углов. С техникой определения величин 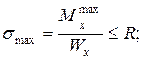
 ,
,


