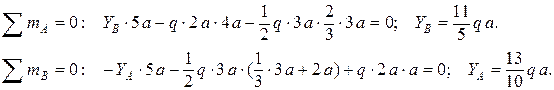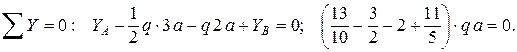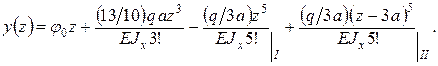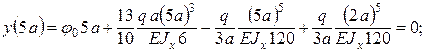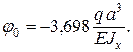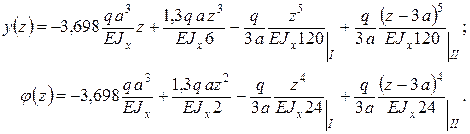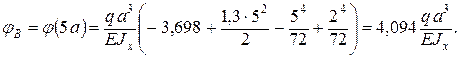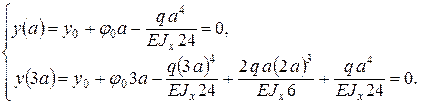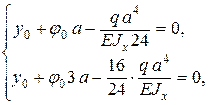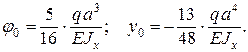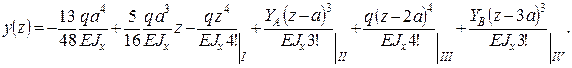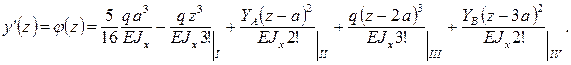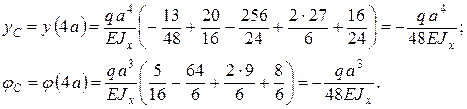Произвольной статической нагрузкой
Аналогичные обозначения вводятся на границах второго и третьего участков (z = а2), третьего и четвертого участков (z = а3) и так Направления всех указанных на рис. 5.3 величин в системе осей координат Оуz считают положительными, то есть при составлении уравнения упругой линии балки их включают со знаком (+). Универсальное уравнение упругой линии для произвольного участка n непрерывной балки, не имеющей промежуточных шарниров, запишем в виде:
Путем дифференцирования уравнения прогибов нетрудно получить универсальное уравнение для углов поворота сечений. Прогибы, направленные вдоль оси Oy, то есть вверх, считаются положительными. А углы поворота сечений положительны, если поперечные сечения в результате деформации балки поворачиваются против хода часовой стрелки. Если начало координат O поместить в правом концевом сечении, ось Oy по-прежнему направить вверх, а ось Oz – вдоль оси балки влево, то моменты, направленные по часовой стрелке, войдут в уравнение со знаком (–), углы αi наклона касательных к эпюре q(z) будут положительны при их отсчете от оси Oz по ходу часовой стрелки. Правила знаков для сил Pi и скачков ∆qi сохраняются теми же, что в правой системе координат. Прогибы, направленные вверх, остаются положительными, а углы поворота сечений будут положительны при повороте сечений по ходу часовой стрелки. Силовые начальные параметры (M0, Q0, q0, q'0) обычно бывают заданы или легко определяются из уравнений равновесия статики (в статически определимых системах). Геометрические же начальные параметры: y0 и j0 – прогиб и угол поворота сечения в начале координат, не показанные на рис. 5.3, – должны быть найдены из граничных условий. При их определении могут встретиться три случая (рис. 5.4). В случае незакрепленного конца балки (рис. 5.4, а) y0 ≠ 0 и j0 ≠ 0. Для их нахождения имеются два условия равенства нулю прогибов в опорных сечениях (y(a) = 0; y(a+ℓ) = 0), из которых и определяют j0 и y0. При этом необходимо решить систему двух алгебраических уравнений относительно j0 и y0. В более простом случае (рис. 5.4, б) y0 = 0 и j0 ≠ 0, и поэтому требуется только одно уравнение для определения неизвестного начального параметра j0, получаемое из условия y(ℓ) = 0.
Рисунок 5.4 – Схемы балок с различными граничными условиями
При заделанном левом концевом сечении (рис. 5.4, в) начальные параметры y0 и j0 равны нулю. Основным преимуществом метода начальных параметров по сравнению с методом непосредственного интегрирования дифференциального уравнения упругой линии является существенное упрощение задачи по определению постоянных интегрирования, так как число неизвестных параметров, подлежащих определению из граничных условий, независимо от числа участков, в статически определимых балках, не превышает двух. После определения неизвестных начальных параметров их значения подставляются в предварительно составленные уравнения прогибов и углов поворота. На этом заканчивается этап формирования уравнений, которые затем применяют для определения перемещений характерных сечений балки. По полученным результатам строятся эпюры прогибов и углов поворота поперечных сечений. Методику решения задач по определению перемещений с помощью универсального уравнения упругой линии рассмотрим на Пример 5.2. Определить прогиб в сечении С и угол поворота сечения В балки (см. рис. 5.2). Решение: задача решена в п. 5.3.1 методом непосредственного интегрирования дифференциального уравнения упругой линии. Решим ее с помощью универсального уравнения. Реакции опор найдены и указаны на расчетной схеме (рис. 5.2). Начало системы осей координат Oyz помещено на левом конце балки. Пользуясь уравнением (5.8) и рисунком 5.2, имеем:
Два первых слагаемых, отделенных первой вертикальной чертой, принадлежат уравнению упругой линии первого участка (0 ≤ z ≤ a). Все три слагаемых, отделенных второй вертикальной чертой, относятся к уравнению второго участка (a ≤ z ≤ ℓ). Это означает, что записанное выражение в компактной форме включает два уравнения упругой линии – для каждого из двух участков балки. Неизвестный начальный параметр j0 определяем из условия
откуда
Знак (–) означает, что сечение повернулось по ходу часовой стрелки. Уравнение упругой линии в окончательном виде:
Дифференцированием функции y(z) получаем уравнение углов поворота сечений:
Полагая z = a, находим прогиб в сечении С:
Знак (–) означает, что центр тяжести сечения С переместился вниз. Угол поворота сечения В находим, приняв z = ℓ:
Сечение В повернулось против хода часовой стрелки. Пример 5.3. Определить прогиб и угол поворота концевого сечения А консольной балки (рис. 5.5).
Рисунок 5.5 – Расчетная схема к примеру 5.3
Решение: в данном случае во избежание решения системы уравнений по определению начальных параметров выберем систему осей координат с началом на правом конце балки. Реакции опоры найдены из уравнений равновесия статики и указаны на расчетной схеме. Балка имеет три участка. По уравнению (5.8) и рисунку 5.5 имеем:
Отсюда дифференцированием получаем:
Поскольку все начальные параметры были известны, полученные уравнения являются окончательными. Полагая z = 4 a, находим:
Центр тяжести сечения А переместился вниз.
Знак (–) указывает на то, что сечение А повернулось против хода часовой стрелки. Пример 5.4. Определить прогиб посредине пролета и углы поворота опорных сечений балки с распределенной нагрузкой переменной интенсивности (рис. 5.6).
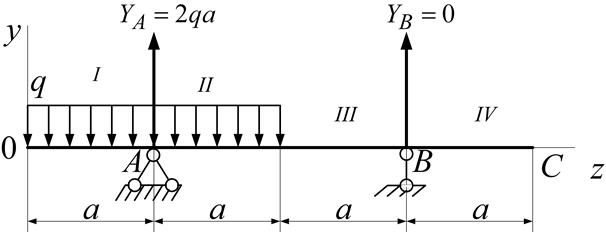
Рисунок 5.6 – Расчетная схема к примеру 5.4
Решение: находим реакции опор по уравнениям равновесия статики:
Проверка:
Начало координат помещаем в левом концевом сечении балки. По уравнению (5.8) и рисунку 5.6 получаем:
Из условия y(5a) = 0 определяем угол поворота j 0 сечения в начале координат:
Универсальные уравнения принимают вид:
Последнее уравнение получено дифференцированием по z функции y(z). Находим прогиб балки в середине пролета (z = 2,5 а):
Угол поворота опорного сечения В (z = 5 а):
Сечение В повернулось против хода часовой стрелки. Пример 5.5. Определить прогиб и угол поворота сечения С двухконсольной балки (рис. 5.7).
Рисунок 5.7 – Расчетная схема к примеру 5.5 Решение: реакции опор определены и указаны на расчетной схеме. Начало системы координат Оyz поместим в левом концевом сечении балки. Составляем уравнение прогибов по выражению (5.8) и ри-
Неизвестные начальные параметры y0 и j 0 определяем из граничных условий y(a) = 0 и y(3a) = 0:
Перепишем полученную систему уравнений относительно y0 и j 0 в виде
откуда
Уравнение прогибов принимает вид:
Уравнение углов поворота сечений:
Полагая z = 4a, находим:
Сечение С переместилось вниз и повернулось по ходу часовой стрелки. Рассмотренные примеры дают достаточное представление о технике формирования уравнений прогибов и углов поворота поперечных сечений балок, их применении к вычислению перемещений.
|

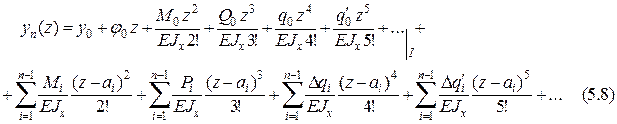

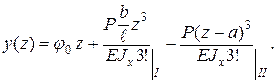
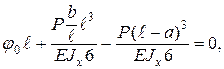
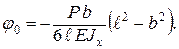
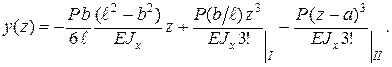
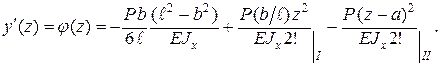
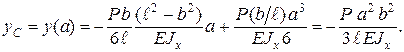
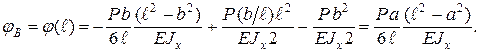

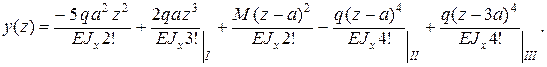
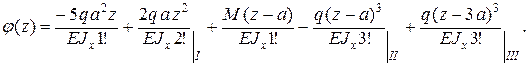
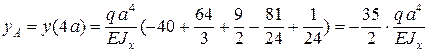 .
.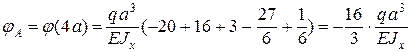 .
.