Упругой линии. Примеры решения задач

Задача определения перемещений при изгибе более просто решается с использованием уравнения изогнутой оси балки, записанного в форме метода начальных параметров. Согласно этому методу, получившему распространение в строительной механике, перемещение любого сечения балки выражается через перемещения и силовые факторы в начале координат – начальные параметры.

Получаемое таким способом уравнение изогнутой оси балки называют универсальным уравнением упругой линии.

Не останавливаясь на выводе этого уравнения, который подробно изложен в учебнике [2], рассмотрим практические приемы его применения при определении перемещений в балках.

На рисунке 5.3 показана схема нагружения балки постоянного сечения произвольной поперечной нагрузкой [2]. Начало координат совмещено с центром тяжести левого концевого сечения, ось Оy направлена вверх, а ось Oz – вдоль оси балки вправо.

Обозначения, принятые на рис. 5.3:

M₀, Q₀, q₀ – изгибающий момент, поперечная сила, интенсивность распределенной нагрузки при z = 0;

α₀ – угол наклона касательной к эпюре q(z) при z = 0, причем
tgα₀ = q'(z)_{|z = 0} = q'₀ – производная от интенсивности распределенной нагрузки при z = 0;

M₁, P₁, ∆q₁ – момент, сила, скачок в интенсивности распределенной нагрузки при z = a₁, то есть при переходе с участка I к участку II. В этом же сечении имеет место скачок в производной от интенсивности распределенной нагрузки: ∆q'₁ = tgα₂ – tgα₁. Скачки могут быть и в последующих производных, то есть , ...

Рисунок 5.3 – Схема нагружения балки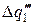