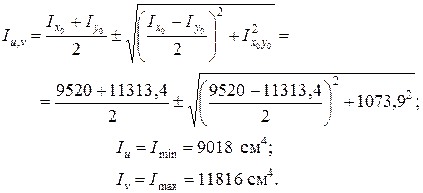Пример решения задачи № 3. Требуется определить главные центральные моменты инерции плоского сечения заданной формы (рис
Требуется определить главные центральные моменты инерции плоского сечения заданной формы (рис. 4.7). Решение: вычерчиваем заданное сечение в масштабе, разбиваем его на элементарные фигуры, которым присваиваем номера: I – прямоугольник, II – треугольник, III – четверть круга. 1. Определение центра тяжести сечения. Обозначаем на чертеже сечения центры тяжести его элементов (Ci) и проводим через них центральные оси, соответственно параллельные между собой. Вычисляем и указываем на чертеже расстояния между осями (см. рис. 4.7). Находим площади элементов сечения:
Площадь заданного сечения:
Определяем положение центра тяжести сечения в системе координат C1x1y1:
Указываем центр тяжести сечения на чертеже (т. С) и проводим через него оси x0, y0, соответственно параллельные осям элементарных фигур. Вычисляем и указываем на чертеже расстояния между осями x0, y0 и соответствующими осями xi, yi.
Размеры в см

Рисунок 4.7 – Нестандартное сечение и его элементы
Проверим вычисления, определив статические моменты сечения относительно осей x0, y0:
Центр тяжести сечения найден верно. 2. Определение осевых и центробежного моментов инерции сечения. Вычисляем осевые и центробежные моменты инерции элементарных фигур (см. рис. 4.7) по соответствующим формулам (см. рис. 4.4):
Находим осевые и центробежный моменты инерции заданного сечения относительно осей x0, y0, пользуясь зависимостями (4.3) и (4.4):
3. Определение положения главных центральных осей и вычисление значений главных центральных моментов инерции сечения.
Следовательно,
Для получения направлений главных центральных осей оси х0, у0 следует повернуть против хода часовой стрелки, так как Вычисляем значения главных центральных моментов инерции сечения:
Проверяем правильность определения величин Iu и Iv:
Главные центральные оси u (min) и v (max) показаны на чертеже (см. рис. 4.7). Рекомендуемая литература
1. Алмаметов, Ф.З. Расчетные и курсовые работы по сопротивлению материалов / Ф.З. Алмаметов, С.И. Арсеньев, С.А. Енгалычев и др. – М.: Высшая школа, 1992. – С. 19-31. 2. Феодосьев, В.И. Сопротивление материалов / В.И. Феодосьев. – М.: Наука, 1986. –С. 121-132. 3. Смирнов, А.Ф. Сопротивление материалов / А.Ф. Смирнов, А.В. Александров, Н.И. Монахов и др. – М.: Высшая школа, 1975. – 4. Кобяков, Е.Т. Определение геометрических характеристик плоских сечений с применением ЭВМ / Е.Т. Кобяков, И.С. Шуев. – Орел: ОФ МИП, 1993. – 26 с.
|








 ;
;  ;
; ;
; .
.




 .
.