Последовательность выполнения задания
1. Определение координат центра тяжести сечения. Заданное сечение разбивают на простые части (элементы), Выбирают систему осей координат Оху, в которой определяют координаты центра тяжести сечения по формулам:
где F, Fi – площади сечения и выделенных частей; xi, yi – координаты центров тяжести Ci элементов сечения в системе осей координат Оху. В качестве системы Оху для нахождения координат центра тяжести сечения может быть выбрана одна из систем Центр тяжести сечения (С) указывают на чертеже и проводят через него две взаимно перпендикулярные оси Cx0 и Cy0, соответственно параллельные осям Cixi и Ciyi выделенных частей, вычисляют и указывают на чертеже расстояния между осями Cx0, Cy0 и соответствующими им центральными осями составляющих элементов. Найденные значения координат центра тяжести С могут быть проверены по формулам:
так как статические моменты В сечениях, заданных к задаче № 1, имеется одна ось симметрии. Следовательно, вычислить нужно только одну координату центра тяжести, так как последний расположен на оси симметрии. 2. Определение осевых и центробежного моментов инерции заданного сечения. По известным формулам для простых сечений (рис. 4.4) вычисляют осевые и центробежные моменты инерции составляющих частей относительно их центральных осей, проведенных на чертеже ( Для прокатных профилей необходимые значения осевых моментов инерции имеются в таблицах стандартов. Центробежный момент инерции элемента относительно центральных осей, одна из которых есть ось симметрии, равен нулю. Если элементы сечения не имеют осей симметрии, их центробежные моменты необходимо вычислить. Следует иметь в виду, что знак центробежного момента инерции зависит от расположения фигуры в системе ее центральных осей (см. рис. 4.4). Если большая часть фигуры расположена в I и III четвертях системы осей координат После определения моментов инерции отдельных частей находят моменты инерции всего сечения относительно центральных осей x0, y0, пользуясь зависимостями:
где ai и bi – соответственно расстояния между осями yi, y0 и xi, x0.
Рсунок 4.4 – К определению осевых и центробежных моментов инерции элементарных фигур
Необходимо помнить, что при вычислении центробежного момента инерции 3. Определение положения главных центральных осей и вычисление значений главных центральных моментов инерции заданного сечения. Если плоское сечение имеет ось симметрии (y0 в задаче № 1), то эта ось есть одна из главных центральных осей, а вторая – перпендикулярна к оси симметрии и проходит через центр тяжести сечения. Поэтому значения главных центральных моментов инерции в этом случае равны В случае несимметричного сечения положение главных центральных осей определяют по формуле
где α0 – угол, на который следует повернуть оси x0, y0, чтобы они совпали с главными, то есть с такими осями u и v, для которых Значения главных центральных моментов сечения определяют по формуле
Главные центральные оси проводят через точку С на чертеже. Ось максимального момента инерции (v) образует меньший угол с той из осей x0, y0, относительно которой момент инерции больше. Для проверки вычислений пользуются следующими зависи-мостями:
Если они соблюдаются, то главные центральные моменты инерции сечения найдены верно при условии, что моменты инерции
|

 , (4.1)
, (4.1) центральных осей составляющих частей.
центральных осей составляющих частей. (4.2)
(4.2) и
и  относительно центральных осей должны быть равны нулю.
относительно центральных осей должны быть равны нулю.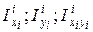 ).
).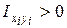 , если же – во II и IV четвертях, то
, если же – во II и IV четвертях, то  .
. (4.3)
(4.3)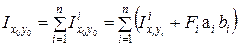 , (4.4)
, (4.4)


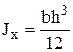
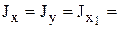





 ;
; 


 значения ai и bi берутся с их знаками (
значения ai и bi берутся с их знаками (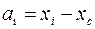 ;
; 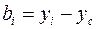 ), то есть а и b рассматриваются как координаты центра тяжести Ci элемента сечения в системе координат
), то есть а и b рассматриваются как координаты центра тяжести Ci элемента сечения в системе координат 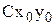 .
. и
и 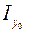 . Один из них есть наименьший (Iu), а второй – наибольший (Iv) из всех моментов инерции относительно центральных осей сечения.
. Один из них есть наименьший (Iu), а второй – наибольший (Iv) из всех моментов инерции относительно центральных осей сечения. , (4.5)
, (4.5) . При
. При  оси x0, y0 надо повернуть против хода часовой стрелки, а при
оси x0, y0 надо повернуть против хода часовой стрелки, а при  – по ходу.
– по ходу. (4.6)
(4.6)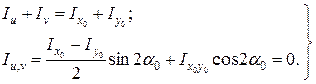 (4.7)
(4.7) также найдены верно.
также найдены верно.


