Пример выполнения задания. Вычерчиваем в масштабе расчетную схему бруса и указываем исходные данные согласно заданному варианту (рис
Вычерчиваем в масштабе расчетную схему бруса и указываем исходные данные согласно заданному варианту (рис. 3.3). (Выписывается текст задания – см. п. 3.1).
Рисунок 3.3 – Расчетная схема бруса
Примечание: при вычерчивании расчетной схемы масштабы длин участков бруса и размеров поперечных сечений допустимо выбирать независимыми. Решение: заданная система один раз статически неопределима. Для раскрытия статической неопределимости отбрасываем правую опору, а ее действие на вал заменяем моментом МВ (рис. 3.4, а). Этот момент определяем из условия равенства нулю угла поворота правого сечения В относительно левого А. Выражение для угла поворота jВ записываем, пользуясь принципом суперпозиции. При этом жесткость на участке АС обозначаем GJk, на участке
Отсюда
Рисунок 3.4 – Расчетная схема и эпюры к расчету вала на кручение
Последнее равенство получено умножением предыдущего на Определим геометрические характеристики крутильной жесткости для каждой ступени вала, пользуясь известными формулами Для прямоугольного сечения (участок АС):
Для кольцевого сечения (участок CD):
Для треугольного сечения (участок DB):
Находим отношения:
Выразим момент МВ через параметр m, используя исходные
Из уравнения равновесия статики
Действительное направление момента МА в данном случае совпало с предполагаемым. Указываем момент МА на расчетной схеме (Если в результате вычислений момент МА будет отрицательным, это означает, что его направление противоположно направлению момента МВ. На расчетной схеме следует указать действительное направление момента МА). Методом сечений строим эпюру крутящих моментов. Для этого вал разбиваем на участки, границами которых являются сечения, где приложены внешние моменты. При этом крутящий момент считаем положительным, если при взгляде на сечение со стороны внешней нормали он направлен против хода часовой стрелки. Из этого правила знаков для крутящих (внутренних) моментов вытекает правило учета знаков внешних моментов при составлении аналитических выражений для крутящих моментов. Крутящий момент в сечении вала равен алгебраической сумме внешних моментов, приложенных по одну сторону от сечения относительно оси вала. Если при взгляде от сечения к концу вала внешний момент направлен по ходу часовой стрелки, то при составлении аналитического выражения для Мк его учитываем со знаком (+). В данном случае вал имеет четыре участка для построения эпюры Мк, которые на рис. 3.4, а пронумерованы римскими цифрами: I, II, III, IV. Составляем аналитические выражения для крутящих моментов по участкам:
Эпюра крутящих моментов в принятом масштабе построена на Построенную эпюру крутящих моментов проверяем по скачкам: в сечениях вала, в которых приложены внешние моменты, на эпюре Мк имеем скачки на величины этих моментов. Построим эпюру максимальных касательных напряжений. Участок I имеет постоянное сечение прямоугольной формы. Опасные точки в этом сечении находятся посередине длинных сторон. Напряжения в этих точках:
где При этом параметр m должен быть выражен в Нм. Коэффициент a выбран по табл. 3 из [1, c. 107]. Такую же форму сечения имеет вал на отрезке ЕС участка II, где
На отрезке CF участка II вал имеет кольцевое сечение. Опасными в этом сечении являются крайние точки, в которых
где Такое же кольцевое сечение имеет вал на отрезке FD участка III, где
На отрезке DK участка III и на участке IV вал имеет треугольное сечение. Опасными точками этого сечения являются точки, расположенные посередине сторон треугольника. При этом [1, с. 119]
Напряжения в опасных точках сечения на отрезке DK участка III и на участке IV соответственно:
По полученным результатам построена эпюра наибольших касательных напряжений по длине вала (рис. 3.4, в). Наибольшие касательные напряжения, как следует из эпюры По условию прочности определяется допускаемое значение параметра m: 6,006×104× m £ [ t ] = 80×106 Па.
Отсюда
Находим допускаемые значения внешних моментов:
Построим эпюру углов поворота поперечных сечений вала при найденных значениях внешних моментов. На участке I крутящий момент положителен. Следовательно, сечение, заданное координатой z 1, повернется по направлению крутящего момента, то есть против хода часовой стрелки, если смотреть на сечение со стороны положительного направления оси z (см.
где z 1 измеряется в метрах (0 £ z 1 £ 0,6 м). В сечении Е Угол поворота сечений от координаты z 1 зависит линейно. Следовательно, на эпюре углов поворота сечений будут отрезки прямых линий. Угол поворота сечения С:
Сечение С относительно сечения А повернулось по ходу часовой стрелки (если смотреть со стороны положительного направления Угол поворота сечения F:
Угол поворота сечения D:
Сечение F и D повернулись относительно сечения А по ходу часовой стрелки. Угол поворота сечения К:
Угол поворота сечения В вычисляем для проверки решения:
Незначительное отклонение от нуля связано с погрешностью вычислений за счет округления результатов. Эпюра углов поворота сечений вала построена на рис. 3.4, г. По эпюре углов поворота поперечных сечений вала находим наибольшее значение относительного угла закручивания, которое имеет место на отрезке DK участка IV:
Это же значение может быть найдено по формуле
Сравнив это значение с допускаемым
Рекомендуемая литература
1. Феодосьев, В.И. Сопротивление материалов / В.И. Феодосьев. – М.: Наука, 1986. – С. 89-120. 2. Миролюбов, И.Н. Пособие к решению задач по сопротивлению материалов / И.Н. Миролюбов, С.А. Енгалычев, Н.Д. Сергиевский и др. – М.: Высшая школа, 1985. – С. 48-61. 3. Александров, А.В. Сборник задач по сопротивлению материалов / А.В. Александров, Б.П. Державин, Б.Я. Лащеников и др. – М.: Стройиздат, 1977. – С. 76-84.
|


 , на участке
, на участке  :
:
 .
.

 и делением на множитель при МВ.
и делением на множитель при МВ.


 ;
; 
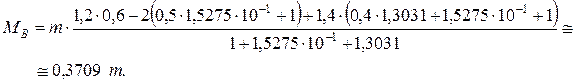
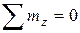 (рис. 3.4, а) находим второй опорный момент МА, предполагая, что его направление совпадает с направлением момента МВ:
(рис. 3.4, а) находим второй опорный момент МА, предполагая, что его направление совпадает с направлением момента МВ: ;
; .
.
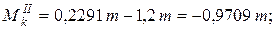

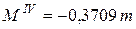 .
.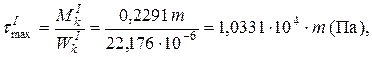


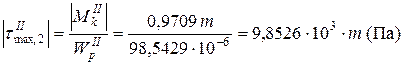 ,
,
 .
.
 ;
; .
. , возникают на отрезке DK участка III вала, имеющего здесь треугольное сечение.
, возникают на отрезке DK участка III вала, имеющего здесь треугольное сечение.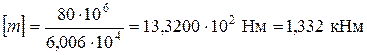 .
. ;
;  ;
;  ;
; ;
;  .
. ,
, .
.




 .
.
 , делаем заключение о достаточной жесткости вала.
, делаем заключение о достаточной жесткости вала.


