Пример решения задачи № 1. Вычерчиваем расчетную схему бруса и указываем исходные данные (рис
Вычерчиваем расчетную схему бруса и указываем исходные данные (рис. 2.3). (Выписываем текст задания - см. п. 2.1). Решение: в результате нагружения бруса в его заделках возникают реакции RA и RB, направленные вдоль его оси. Составляем уравнение равновесия статики:
Это уравнение является единственным уравнением статики и содержит две неизвестные силы. Следовательно, система один раз статически неопределима. Для составления уравнения перемещений отбросим мысленно нижнюю опору В и заменим ее действие на брус реакцией RB, которую принимаем за основную неизвестную силу X 1: RB = X 1 (рис. 2.4).
а = 0,2 м; Р = 100 кН; Р 1 = 0,8 Р; Р 2 = 1,2 Р; F 1 = 1,2 F; F 2 = 2,8 F; материал – чугун, [ s ] p = 40 МПа; [ s ] с = 90 МПа; Е = 1,3 × 105 МПа; a = 10 × 10-6.
Рисунок 2.3 – Расчетная схема бруса к задаче № 1
Полученная система должна быть эквивалентна заданной, откуда следует, что перемещение сечения В должно быть равно нулю, так как в заданной системе это сечение не перемещается:
Рисунок 2.4 – Эпюры нормальных сил N, нормальных напряжений s и перемещений d поперечных сечений
Воспользовавшись принципом независимости действия сил и формулой
откуда, подставляя исходные данные, имеем:
Статическая неопределимость раскрыта. Реакцию
Знак (–) означает, что реакция RA имеет направление, обратное показанному на рис. 2.3. Учитывая, что Р = 100 кН, имеем: RA = – 34 кН; RB = 74 кН. Пользуясь методом сечений, строим эпюру нормальных сил, составив аналитические выражения N для каждого участка (рис. 2.4):
Для построения эпюры нормальных напряжений имеем соответствующие аналитические выражения:
Подбор сечений бруса в данном случае осуществляем по условию прочности второго участка, так как на этом участке возникают наибольшие растягивающие напряжения:
откуда
Принимаем По найденному значению параметра F определяем площади сечений участков бруса:
Подбор сечений чугунного бруса по условию прочности на сжатие в данном случае не нужен, так как наибольшие значения сжимающих напряжений (0,2833 P / F) меньше растягивающих (0,3833 P / F), а (Если же значения сжимающих напряжений окажутся больше растягивающих, следует найти параметр F по двум условиям прочности: на растяжение и сжатие, а затем принять большее из найденных значений F. В случае стального бруса подбор сечений производится по наибольшему по абсолютной величине напряжению). Определяем изменения длин участков бруса:
Проверяем вычисления по условию
которое подтверждает справедливость найденных результатов. Находим осевые перемещения сечений бруса по границам участков. Перемещения, направленные вниз от опоры А, считаем положительными.
При Р = 100 кН и F = 9,60 см2, найденном по условию прочности, имеем:
Эпюра осевых перемещений показана на рис. 2.4. Определим, каким должно быть изменение температуры стержня, чтобы реакция RB стала равной нулю (X = RB = 0). В этом случае вместо уравнения (2.2) имеем:
где ℓ; = 4 а – длина стержня; α; – коэффициент линейного расширения материала. Отсюда
Эпюры N, s и δ для этого случая построены на рис. 2.5. Условия работы бруса ухудшились, так как напряжения существенно возросли.
Рисунок 2.5 – Схема бруса и эпюры N, s, d в случае RВ = 0 (согласно п. 5 задания)
Определим допускаемую нагрузку при прежнем значении параметра F = 9,6 см2:
Допускаемая нагрузка на систему уменьшилась в 2,6 раза:
Построим эпюру продольных перемещений сечений бруса при этих значениях внешних воздействий, пользуясь следующими зависимостями:
Последнее выражение служит для проверки В данном случае
Следовательно,
Эпюра δ построена на рис. 2.5. Сделанный расчет показывает, что распределение напряжений между участками статически неопределимой системы существенно зависит от возможных изменений температуры. Статически определимые конструкции этим свойством не обладают. Примечания (для студентов строительных специальностей): 1. Подбор сечений бруса в рассмотренном примере при расчете по методу предельных состояний следует производить по условию прочности:
где Rp – расчетное сопротивление при растяжении, а параметр Р характеризует расчетную нагрузку (Р = 100 кН). 2. Под допускаемой нагрузкой, определяемой по п. 6 задания к задаче № 1, следует понимать допускаемое значение расчетной нагрузки, рассчитываемое по условию прочности. 2.3.2 Пример решения задачи № 2
Вычерчиваем расчетную схему стержневой системы в масштабе и указываем исходные данные (рис. 2.6, а). (Выписывается текст задания – см. п. 2.1). Решение: 1. Составим уравнения равновесия статики для балки АВ, введя в рассмотрение усилия в стержнях № 1 и 2 (рис. 2.6, б):
откуда
(Два других уравнения: Задача один раз статически неопределима. Дополнительное уравнение получим, рассмотрев геометрическую картину перемещений (рис. 2.6, в):
где
Тогда из (2.5):
Уравнение совместности деформаций (2.6) записываем в физической форме:
откуда Учитывая, что
Решая систему уравнений (2.4) и (2.7), получаем:

Рисунок 2.6 – Расчетные схемы к задаче № 2 Итак, при Р = 30 кН и 2. Для подбора сечений стержней воспользуемся условиями прочности:
откуда
При этом должно быть Принимаем F 2 = 1,26 см2, 3. Проверяем напряжения в стержнях:
4. Из выражений (2.8) следует, что с увеличением отношения (В статически определимых системах усилия элементов не зависят от соотношения их жесткостей. Поэтому сделанный вывод характеризует общее свойство статически неопределимых систем). При N 1 = 3,97 кН; N 2 = – 19,49 кН, что согласуется с отмеченным свойством статически неопределимых систем. 5. Определим усилия и напряжения в стержнях, возникающие при охлаждении стержня № 1 ( Согласно принципу суперпозиции, эта задача может быть рассмотрена независимо от задачи определения усилий в стержнях от действия нагрузки Р (см. п. 1). Уравнение равновесия статики получим из (2.4), полагая Р = 0:
Для составления уравнения совместности деформаций воспользуемся геометрической картиной перемещений (рис. 2.6, г):
где
Причем
|

 . (2.1)
. (2.1)
 .
.
 , запишем это условие в развернутом виде (см.
, запишем это условие в развернутом виде (см.  , (2.2)
, (2.2) ;
; .
. находим из уравнения статики (2.1):
находим из уравнения статики (2.1): .
.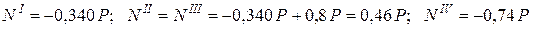 .
.

 ,
, .
. .
.
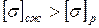 .
.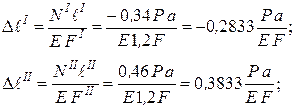

 ,
,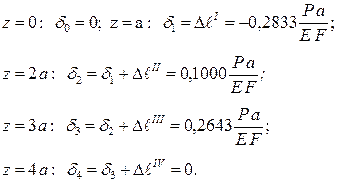
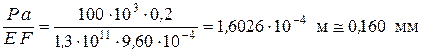 ;
; .
.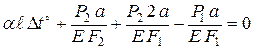 , (2.3)
, (2.3)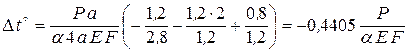 .
.
 ;
;  .
. ;
;

 .
.

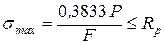 ,
, ,
, . (2.4)
. (2.4) и
и 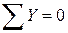 не записываем, так как в них войдут реакции опоры балки, то есть XA, YA, которые по заданию определять не требуется).
не записываем, так как в них войдут реакции опоры балки, то есть XA, YA, которые по заданию определять не требуется). , (2.5)
, (2.5) .
. . (2.6)
. (2.6) ,
,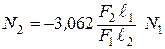 .
. и
и  , имеем:
, имеем: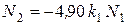 . (2.7)
. (2.7)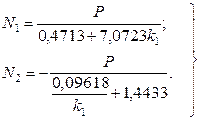 (2.8)
(2.8) N 1 = 2,053 кН (стержень растянут); N 2 = – 20,115 кН (стержень сжат). (Найденные значения проверяем по (2.4)).
N 1 = 2,053 кН (стержень растянут); N 2 = – 20,115 кН (стержень сжат). (Найденные значения проверяем по (2.4)).




 , то есть при увеличении жесткости второго стержня (или при уменьшении жесткости первого стержня) усилие в стержне № 2 возрастает, а в стержне № 1 уменьшается: происходит перераспределение нагрузки.
, то есть при увеличении жесткости второго стержня (или при уменьшении жесткости первого стержня) усилие в стержне № 2 возрастает, а в стержне № 1 уменьшается: происходит перераспределение нагрузки. из (2.8), заменив k 1 = 2 на k 2 = 1, полагая Р = 30 кН, имеем:
из (2.8), заменив k 1 = 2 на k 2 = 1, полагая Р = 30 кН, имеем: ).
). . (2.9)
. (2.9)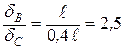 ,
, .
. ;
;  .
.


