Для плоских рам
Рамой называют строительную конструкцию, элементы которой имеют форму бруса (стержня) и работают в основном на изгиб или изгиб с кручением. Соединение стержней рамы между собой осуществляется жесткими узлами. Поэтому изгиб одного из участков рамы вызывает деформацию других, связанных с ним участков. В частном случае оси всех элементов рамы, оси симметрии их поперечных сечений (или главные центральные оси), а также все внешние силы могут лежать в одной плоскости. Такая рама называется плоской. Очевидно, что деформированная ось рамы будет лежать в той же плоскости. Ось поперечного сечения элемента плоской рамы, лежащую в ее плоскости, обозначим y, а вторую ось сечения – x. В поперечных сечениях плоской рамы могут возникать только три внутренних силовых фактора: нормальная сила (N), поперечная сила (Qy) и изгибающий момент (Mx). На рисунке 1.12 показана расчетная схема плоской рамы и направления внутренних силовых факторов в одном из ее сечений, считающиеся положительными. Обозначения реакций опор не связаны с обозначениями осей поперечного сечения. Рама отнесена к системе осей координат Оxу, в которой ось Ох горизонтальна, а ось Оу вертикальна, что и дает обозначения составляющих реакций опор: ХА, УА, УВ (ХВ = 0). Правило знаков для N и Qy остается без изменений
Рисунок 1.12 – Пример расчетной схемы плоской рамы
Чтобы избежать этого неудобства, условимся обход контура рамы при записи аналитических выражений совершать изнутри и сто-
Поскольку каждый элемент рамы можно рассматривать как балку (балочный элемент), то составление аналитических выражений внутренних силовых факторов осуществляется по тем же правилам, что для стержней и балок (см. пп. 1.1 и 1.3). Построение эпюр N, Qy, Mx производится на контурах, которые вычерчиваются в том же масштабе, что и контур расчетной схемы рамы, и полностью повторяют его форму (всего вычерчивают три контура – по числу подлежащих построению эпюр). Эти контуры (оси эпюр) должны размещаться обязательно на одной странице с чертежом расчетной схемы рамы. Положительные значения ординат эпюр N и Qy откладывают снаружи контура, отрицательные – внутри. Значения изгибающих моментов откладывают со стороны сжатых волокон элемента рамы (это соответствует правилу: (+) – вверх, (–) – вниз) и поэтому знаки на эпюре Мх не указывают. Штриховку выполняют в направлении отложенных ординат, то есть перпендикулярно к оси рамы. (Студенты строительных специальностей строят эпюру Мх «на растянутых волокнах»). Рассмотрим примеры построения эпюр N, Qy, Mx для плоских рам. Пример 1.6. Построить эпюры внутренних силовых факторов для бруса с ломаной осью (рис. 1.13, а).

Рисунок 1.13 – Расчетная схема и эпюры N, Qy, Mx к примеру 1.6
Решение: реакции опоры в данном случае можно не определять, если рассматривать отсеченную часть со стороны незакрепленного конца бруса. Разбивка на участки и координаты произвольных сечений каждого участка показаны на рисунке 1.13, а. Границами участков являются узлы (в данном случае узел К) и точки приложения внешних сил. Записываем аналитические выражения нормальных сил N по участкам согласно правилу (см. п.1.1):
Строим эпюру (см. рис. 1.13, б). Записываем аналитические выражения поперечных сил Qy, воспользовавшись правилом, сформулированным в п. 1.3:
Строим эпюру Qy (см. рис. 1.13, в). Составляем аналитические выражения изгибающих моментов по правилу (см. п. 1.3):
0 £ z 4 £ 0,8 ℓ;.
Производим вычисления и строим эпюру Mx (см. рис. 1.13, г):
Проверка построенных эпюр производится по правилам, указанным в п. 1.3 и примере 1.3, применительно к каждому элементу рамы. Во избежание ошибок можно также проверить равновесие узла К (см. рис. 1.13, а), вырезав этот узел и приложив в сечениях, примыкающих к узлу, силовые факторы, взятые с эпюр N, Qy, Mx Пример 1.7. Построить эпюры внутренних силовых факторов для рамы (рис. 1.14, а).
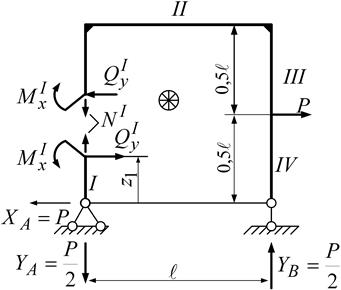
Рисунок 1.14 – Расчетная схема рамы и эпюры N, Qy, Mx к примеру 1.7 Решение: определяем реакции опор:
откуда
откуда
Разбиваем раму на участки, на каждом из которых проводим произвольное сечение и указываем его координату zi (см. рис. 1.14, а). Записываем аналитические выражения нормальных сил, пользуясь правилом, указанным в п.1.1:
Эпюра N показана на рисунке 1.14, б. Записываем аналитические выражения поперечных сил, руковод-ствуясь правилом, данным в п.1.3:
Эпюра Qy построена на рисунке 1.14, в. Составляем аналитические выражения изгибающих моментов по правилу, сформулированному в п. 1.3:
Производим вычисления изгибающих моментов в характерных сечениях:
По полученным значениям строим эпюру Мх (рис. 1.14, г). Производим проверку построенных эпюр, пользуясь правилами, указанными в п. 1.3 и примере 1.3, применительно к каждому элементу рамы, а также проверяем равновесие узлов рамы (см. рис. 1.14, д). Пример 1.8. Построить эпюры внутренних силовых факторов для рамы с криволинейными участками (рис. 1.15, а). Решение: определяем реакции опор:
откуда
откуда
Проверка: – YА + YВ = 0. Значения реакций опор указываем на чертеже. Разбиваем раму на участки и проводим на каждом участке произвольное поперечное сечение (см. рис. 1.15, а). В отличие от прямолинейного участка, положение поперечного сечения которого определяется координатой z, на криволинейных участках вводим угловую координату j, отсчет которой ведем от начала участка.
а

Рисунок 1.15 – Расчетная схема и эпюры к примеру 1.8 Перед составлением аналитических выражений N, Qy, Mx удобно внешние силы, приложенные по одну сторону от сечения криволинейного участка, разложить на их составляющие, одна из которых направлена по нормали к сечению, а другая – по направлению сечения (оси n и t – см. рис. 1.15, а). Разложения сил показаны на рис. 1.15, а. Они облегчают получение аналитических выражений N и Qy. Для составления выражений изгибающего момента Mx эти разложения не требуются. Аналитические выражения N, Qy, Mx составляются по тем же правилам, что и для рам с ломаной осью (см пп. 1.1, 1.3, 1.5). В данном случае имеем:
По этим выражениям производятся вычисления внутренних силовых факторов в характерных сечениях и строятся эпюры N, Qy, Mx
|

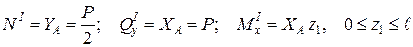 .
.
 .
.
 .
. 0 £ z 1 £1,6 ℓ;;
0 £ z 1 £1,6 ℓ;;  ;
; , 0 £ z 3 £ ℓ;;
, 0 £ z 3 £ ℓ;; ,
,

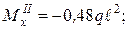



 .
.

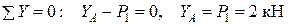 ;
; ,
, .
. ,
, .
. (проверка):
(проверка):
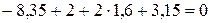 .
. ;
; .
.