Примеры построения эпюр для балок
При прямом (плоском) изгибе бруса, то есть изгибе, при котором изогнутая ось бруса располагается в плоскости действия нагрузки, в поперечных сечениях возникают два внутренних силовых фактора: поперечная сила Qy и изгибающий момент Mx (см. рис. 1.3). Иногда поперечная сила может отсутствовать. Изгиб называют в этом случае чистым (Qy = 0). При Qy ¹ 0 изгиб является поперечным. Брус, в основном работающий на прямой (чистый или поперечный) изгиб, называют балкой. Определим, применяя метод сечений, внутренние силовые факторы в поперечных сечениях балки (рис. 1.7). Балка имеет два участка. Произвольным сечением, положение которого задаем координатой z 1, рассечем балку на первом участке и рассмотрим равновесие левой отсеченной части. Чтобы уравновесить внешнюю силу P, правая (отброшенная) часть балки должна действовать на рассматриваемую (левую) часть силой
Рисунок 1.7 – Схема нагружения балки при поперечном изгибе и эпюры Qy и Мх
Из уравнений равновесия, составленных для левой отсеченной части первого участка: S Y = 0: Р – получаем аналитические выражения для
Аналогично, проведя сечение на участке II и задав его положение координатой z 2, рассматриваем левую отсеченную часть балки и из уравнений равновесия: S Y = 0: P – 2 P – Q получаем аналитические выражения для Q Q Прежде чем сформулировать правила, по которым составляются аналитические выражения для Qy и Mx, условимся считать указанные на рис. 1.7 направления внутренних силовых факторов положительными. Поперечная сила Qy положительна, если она стремится повернуть отсеченную часть балки по ходу часовой стрелки (относительно любой точки, принадлежащей отсеченной части). Изгибающий момент Мх положителен, если он вызывает сжатие верхних волокон балки и растяжение нижних (рис. 1.8).
Рисунок 1.8 – Правила знаков для Qy и Mx
Из принятого правила знаков для Qy и Mx вытекает правило учета знаков внешних сил и их моментов при записи соответствующих аналитических выражений. Поперечная сила Qy в произвольном поперечном сечении бруса равна алгебраической сумме проекций всех внешних сил, приложенных по одну сторону от этого сечения, на плоскость сечения. При этом внешние силы, стремящиеся повернуть отсеченную часть бруса по ходу часовой стрелки (относительно центра сечения), записывают со знаком (+), против часовой стрелки – со знаком (–). Изгибающий момент Мх в произвольном поперечном сечении равен алгебраической сумме моментов всех внешних сил, расположенных по одну сторону от сечения, относительно центра тяжести этого сечения (то есть относительно оси x, проходящей через центр тяжести сечения перпендикулярно к плоскости нагрузки). При этом моменты внешних сил, вызывающих изгиб отсеченной части (относительно мысленно защемленного сечения) вогнутостью вверх, записывают со знаком (+), вогнутостью вниз – со знаком (–). Сформулированные правила позволяют записывать аналитические выражения Qy и Mx для каждого участка непосредственно по чертежу расчетной схемы балки, не прибегая к вычерчиванию ее отсеченных частей. Записанные выражения Q Примечания: 1. Если балка нагружена только сосредоточенными силами и моментами, то эпюра Qy состоит из прямоугольников, а эпюра Mx при поперечном изгибе очерчена наклонными прямыми. 2. В сечениях, в которых приложены сосредоточенные силы, на эпюре Qy имеем скачки, равные значениям этих сил, а на эпюре 3. В сечениях, в которых приложены внешние моменты, на эпюре Мх имеем скачки, равные значениям этих моментов (см. рис. 1.7). 4. В связи с установившимися традициями студенты строительных специальностей должны строить эпюру Мх на «растянутом волокне», то есть положительные значения Мх откладывать вниз от оси балки, а отрицательные – вверх. Рассмотрим примеры построения эпюр Qy и Mx для балок. Пример 1.3. Для нагруженной балки, заделанной одним концом (рис. 1.9), построить эпюры Qy и Mx.
Рисунок 1.9 – Расчетная схема и эпюры к примеру 1.3 Решение: балка имеет три участка. На каждом участке указываем произвольное сечение и отмечаем его положение координатой zi, отсчет которой ведем от начала участка. Составляем аналитические выражения поперечных сил по участкам (см. п. 1.3): Q При составлении выражения для Q На первом и третьем участках поперечная сила не зависит от положения сечения, то есть является постоянной. На втором участке Q Q Эпюра Qy построена (см. рис. 1.9). Определим координату
Q В этом сечении ( Составляем аналитические выражения изгибающих моментов M M Выражения М Вычисляем значения ординат эпюры Mx:
Производим построение эпюры Mx в выбранном масштабе. Осуществляем проверку построенных эпюр. При этом руководствуемся правилами, изложенными в замечаниях к п.1.3. Кроме того, из дифференциальных зависимостей:
1. На участках, на которых нет распределенной нагрузки (q = 0), эпюра Qy – прямоугольная, а на эпюре Mx имеем наклонные прямые. 2. На участках с равномерно распределенной нагрузкой 3. В сечениях, в которых Qy = 0, на эпюре Мх имеем экстре-мумы. 4. На участках, на которых Qy > 0, функция Мх (z) – возрастающая (слева направо); на участках, где Qy < 0, функция Mx (z) – убывающая; на участках с Qy = 0 Мх = const (чистый изгиб). Отмеченные свойства эпюр удобны для контроля правильности их построения. Пример 1.4. Построить эпюры Qy и Мх для двухопорной балки с консолью (рис.1.10). Решение: определяем реакции oпop:
Проверяем найденные значения реакций опор по уравнению проекций всех сил на вертикальную ось:
Разбиваем балку на участки. Границами участков являются точки приложения внешних сил. На каждом участке указываем координату произвольного поперечного сечения, отсчет которой ведем от начала участка: 0 £ z 1 £ 0,2 м; 0 £ z 2 £ 0,4 м; 0 £ z 3 £ 0,2 м; 0£ z 4 £ 0,2 м.
На участках III и IV отсчет координат ведем справа налево. Координату произвольного сечения указывают с той стороны от проведенного сечения, к которой приложено меньше внешних сил: это упрощает аналитические выражения внутренних силовых факторов. Отсчет координаты z текущего сечения можно производить и от общего начала, например, от левого конца балки, но при этом несколько усложняются запись аналитических выражений и соответствующие вычисления.
Рисунок 1.10 – Расчетная схема и эпюры Qy и Мх
Записываем аналитические выражения поперечных сил по общему правилу (см. п. 1.3):
Производим вычисления и строим эпюру Qy:
Координаты
откуда
Составляем аналитические выражения изгибающих моментов
Производим вычисления изгибающих моментов в характерных сечениях:
По полученным значениям строим эпюру Мх (см. рис. 1.10). Проверку построенных эпюр Qy и Мх производим по правилам, изложенным в п.1.3 и примере 1.4. Примечание: в случае отсчета координаты z произвольного сечения каждого участка от общего начала (левого концевого сечения балки) аналитические выражения внутренних силовых факторов имеют вид:
– участок I (0 £ z £ 0,2 м):
– участок II (0,2 м £ z £ 0,6 м):
– участок III (0,6 м £ z £ 0,8 м):
– участок IV (0,8 м £ z £ 1 м):
Аналитические выражения Qy и Мх второго и последующих участков полностью включают соответствующие выражения Qy и Мх предыдущего по номеру участка, к которым добавляются слагаемые, учитывающие влияние нагрузки, приложенной в начале рассматриваемого участка. Поэтому составленные аналитические выражения можно записать в компактной форме:
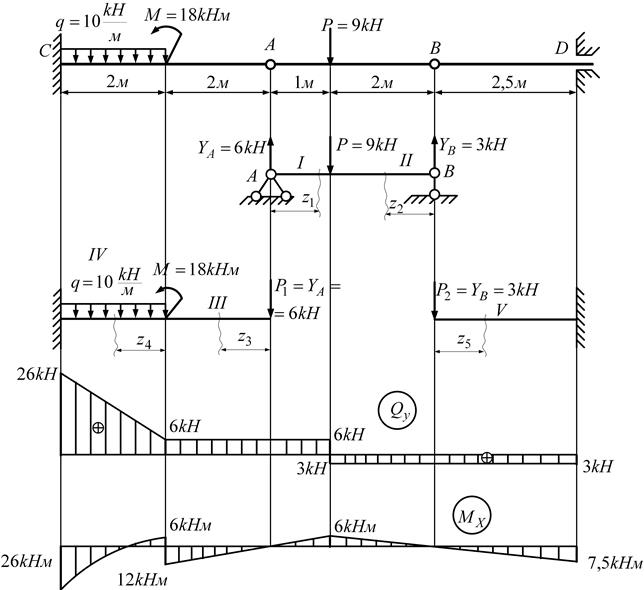
Применение этих выражений при «ручном» построении эпюр целесообразно при небольшом количестве участков, так как с увеличением числа участков быстро растет объем вычислений. Однако при использовании ЭВМ универсальные выражения для Qy и Мх более удобны, так как они позволяют автоматизировать процесс построения эпюр в силу того, что легко программируются. Пример 1.5. Построить эпюры Qy и Мх балки с промежуточными шарнирами (рис. 1.11). Решение: данная балка статически определима. Расчет начинаем с расчленения системы на составные части. Средняя часть балки АВ не может работать самостоятельно, так как является подвесной. Она опирается на несущие балки АС и ВД в шарнирах А и В. Вначале производится определение реакций опор УА и УВ подвесной балки по уравнениям равновесия статики, составленным для этой балки. В данном случае УА = 6 кН, УВ =3 кН. Несущие балки АС и ВД помимо приложенной к ним нагрузки (на балке ВД она отсутствует) воспринимают действие сил Р 1 и Р 2, соответственно численно равных реакциям УА и УВ подвесной балки и противоположно им направленных (см. рис. 1.11). Определение реакций опор несущих балок АС и ВД в данном случае необязательно, так как эти балки являются консолями, и их расчет может быть выполнен со стороны незакрепленного конца. Если же несущие балки имеют шарнирные опоры, то перед построением эпюр Qy и Мх производится определение реакций их опор.
Рисунок 1.11 – Расчетная схема и эпюры Qy и Мх к примеру 1.5
После того как определены все необходимые для составления аналитических выражений силы, производится разбивка балок на участки, отмечается положение произвольных сечений координатами zi на каждом участке, и составляются аналитические выражения поперечных сил и изгибающих моментов по участкам так же, как это делалось в примерах 1.3, 1.4:
По составленным выражениям Qy и Мх производятся вычисления их значений в характерных сечениях (начало и конец участка и точки экстремума) и строятся эпюры (см. рис. 1.11). Проверка построенных эпюр осуществляется по правилам, указанным в п. 1.3 и примере 1.4.
|

 и моментом
и моментом  . Согласно закону действия и противодействия, левая часть балки действует на отброшенную правую часть такими же по значению, но противоположно направленными силовыми факторами
. Согласно закону действия и противодействия, левая часть балки действует на отброшенную правую часть такими же по значению, но противоположно направленными силовыми факторами  и
и 

 = 0 и S mх = 0: Р (ℓ; + z 2) – 2 P z 2 + M – M
= 0 и S mх = 0: Р (ℓ; + z 2) – 2 P z 2 + M – M  = 0
= 0
 , Q
, Q  , M
, M 
 = P – 3 qa = – 2 qa.
= P – 3 qa = – 2 qa. будет наклонная прямая, которую строим по двум точкам:
будет наклонная прямая, которую строим по двум точкам: (3 a) = P – 3 qa = – 2 qa.
(3 a) = P – 3 qa = – 2 qa. – сечения, в котором Q
– сечения, в котором Q 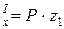 , 0 £ z 1 £ a; M
, 0 £ z 1 £ a; M  0 £ z 2 £ 3 a;
0 £ z 2 £ 3 a; , 0 £ z 3 £ 2 a.
, 0 £ z 3 £ 2 a.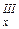 являются линейными функциями координаты текущего сечения (координата z входит в первой степени). Поэтому на эпюре Мх в пределах участков I, III имеем наклонные прямые, которые строим по двум точкам. Выражение М
являются линейными функциями координаты текущего сечения (координата z входит в первой степени). Поэтому на эпюре Мх в пределах участков I, III имеем наклонные прямые, которые строим по двум точкам. Выражение М 
 ;
;
 ;
;  ;
;
 .
.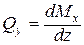 и
и  следует:
следует:

 ;
;



 .
.

 ;
; ;
;  ;
;
 .
. и
и 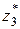 (см. рис. 1.10), при которых Qy = 0, находим из условий:
(см. рис. 1.10), при которых Qy = 0, находим из условий: ;
; 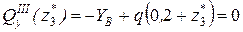 ,
,




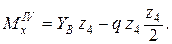
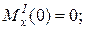
 ;
;  ;
; ;
; ;
; ;
; ;
; ;
;
 .
.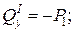
 ;
;
 ;
;
 ;
;






 0 £ z 4 £ 2 м;
0 £ z 4 £ 2 м; 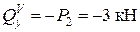 .
. ; 0 £ z 1 £ 1 м;
; 0 £ z 1 £ 1 м;  ; 0 £ z 2 £ 2 м;
; 0 £ z 2 £ 2 м; ; 0 £ z 3 £ 2 м;
; 0 £ z 3 £ 2 м; 0 £ z 4 £ 2 м;
0 £ z 4 £ 2 м; ; 0 £ z 5 £ 2,5 м.
; 0 £ z 5 £ 2,5 м.


