Нагружении. Примеры построения эпюр нормальных сил

 

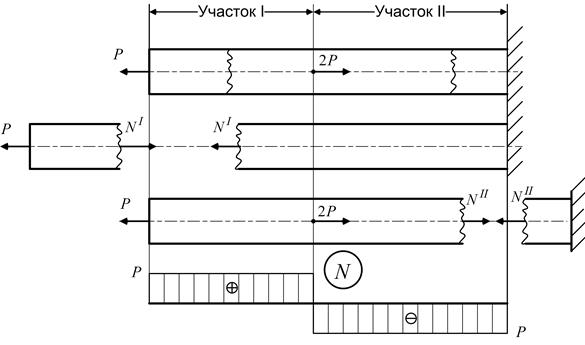
Применяя метод сечений к брусу (рис. 1.4), определим внутренние силовые факторы в его поперечных сечениях.

Рассечем брус поперечным сечением на участке между точками приложения сил Р и 2 P (участок I) и рассмотрим равновесие левой отсеченной части. Для равновесия этой части бруса достаточно, чтобы в сечении возникал только один внутренний силовой фактор – нормальная сила N^I (верхний индекс указывает номер участка). Из уравнения равновесия S Z = 0, то есть – P + N^I = 0, следует N^I = Р.

 

Рисунок 1.4 – Схема осевого нагружения бруса и эпюра нормальных сил

 

 

Аналогично получаем аналитическое выражение для нормальной силы участка II. Из уравнения равновесия: – Р + 2 Р + N^II = 0 находим N^II = Р – 2 P = – Р. Остальные внутренние силовые факторы в поперечных сечениях равны нулю (отсутствуют).

Аналитические выражения нормальных сил N^I и N^II показывают, что их значения не зависят от положения сечения в пределах соответствующего участка.

Для построения эпюры N проводим прямую, параллельную оси бруса, иногда называемую осью эпюры, и от нее откладываем значения ординат, то есть значения нормальных сил: положительные – вверх, отрицательные – вниз (см. рис. 1.4).

Эпюры принято штриховать: штриховка должна быть перпендикулярна к оси эпюры – каждая линия штриховки (ордината) в принятом масштабе дает значение нормальной силы в соответствующем поперечном сечении бруса.

Для нормальных сил вводится правило знаков: нормальная сила положительна при растяжении (направлена oт сечения) и отрицательна при сжатии (направлена к сечению).

На рис. 1.4 нормальные силы N^I и N^II показаны положительными, но при вычислении оказалось, что N^II < 0. Это значит, что в действительности сила N^II – сжимающая, то есть направлена к сечению, а участок II испытывает деформацию сжатия.

Структура выражений N^I = P и N^II = P – 2 P позволяет сформулировать правило составления аналитических выражений для нормальных сил:

нормальная сила в поперечном сечении бруса равна алгебраической сумме проекций на ось бруса внешних сил, приложенных на одну сторону от рассматриваемого сечения. При этом внешние силы, направленные от сечения (растягивающие), берут со знаком (+), а направленные к сечению (сжимающие) – со знаком (–), что вытекает из принятого правила знаков для N.

Полученное правило позволяет записывать выражения для нормальных сил непосредственно по расчетной схеме, не прибегая к вычерчиванию отсеченных частей бруса.

Примечания:

1. Если брус нагружен только сосредоточенными силами, то эпюра N состоит из прямоугольников.

2. В сечениях бруса, в которых приложены внешние силы, на эпюре N имеют место скачки, численно равные этим силам.

3. Прямой брус, работающий на растяжение или сжатие, называют стержнем.

Рассмотрим примеры построения эпюр нормальных сил.

Пример 1.1. Для стержня, находящегося в равновесии под действием заданной системы внешних сил, построить эпюру нормальных сил (рис. 1.5).

Решение: разбиваем брус на участки. Границами участков I, II, III, IV являются сечения, в которых приложены внешние силы.

Проводим произвольное сечение и составляем выражение для нормальной силы каждого участка, пользуясь правилом, изложенным выше: N^I = 20 кH, N^II = 20 – 10 = 10 кН (по левой отсеченной части), N^III = 5 – 25 = – 20 кН (по правой отсеченной части), N^IV = 5 кН.

Строим эпюру, указывая значения всех характерных ординат
(рис. 1.5).

 

 

Рисунок 1.5 – Расчетная схема

и эпюра N к примеру 1.1

 

Проверяем правильность построения эпюры (см. примечания к п.1.2.1)

Пример 1.2. Для бруса (рис. 1.6) построить эпюру N с учетом собственного веса бруса. Площадь поперечного сечения на первом участке равна F, а на втором – 2 F. Удельный вес материала – g.

 

 

Рисунок 1.6 – Расчетная схема и эпюра N к примеру 1.2

Решение: собственный вес бруса в пределах каждого участка является равномерно распределенной нагрузкой, которая характеризуется интенсивностью q.

Для первого и второго участков соответственно имеем:

 

, ,

где G ₁, G ₂, – силы тяжести участков I и II, ℓ;₁ и ℓ;₂ – их длины.

Проводим произвольное сечение на участке I и отмечаем его положение координатой z ₁.

По общему правилу (см. п. 1.2.1) составляем аналитическое выражение для нормальной силы первого участка (см. рис. 1.6):

 

N^I = – Р – q ₁ z ₁,

откуда следует, что N^I является линейной функцией координаты z ₁, изменяющейся в пределах: 0 £ z ₁ £ ℓ;.

Производим вычисления и строим эпюру N для первого участка (см. рис. 1.6):

N^I (0) = – Р; N^I (ℓ;) = – P – q ₁ ℓ; = – P – g F ℓ;.

Аналогично составляем аналитическое выражение для нормальной силы второго участка. Отсчет координаты z ₂ текущего сечения производим от начала участка:

N^II = – P – q ₁ ℓ; – P – q ₂ z ₂, 0 £ z ₂ £ ℓ;.

Находим значения N^II в крайних сечениях и строим эпюру N для второго участка:

N^II (0) = – 2 P – g F ℓ;; N^II (ℓ;) = – 2 P – 3 g F ℓ;.

Проверяем правильность построенной эпюры по скачкам.

Примечание: отсчет координаты z, определяющей положение произвольного сечения, может быть сделан и от общей базы, в данном случае – от верхнего торца бруса. Следует иметь в виду, что в этом случае пределы изменения координаты z будут другими.

Для примера 1.2 имеем:

N^I = – P – q ₁ z, 0 £ z £ ℓ;;

N^II = – P – q ₁ ℓ; – P – q ₂ (z – ℓ;), ℓ; £ z £ 2 ℓ;.