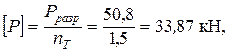Тогда ; .
Отсюда
или Решив систему уравнений (2.9) и (2.10), находим: N 1 = 1829 Н ≈ 1,83 кН; N 2 = 597,4 Н ≈ 0,597 кН. Оба стержня растянуты. Соответствующие температурные напряжения:
Действительные напряжения в стержнях равны сумме напряжений от действия нагрузки и температурных напряжений (см. п. 3):
Наличие температурных напряжений заметно изменило значения напряжений в стержнях. (Возникновение температурных напряжений является свойством статически неопределимых систем. В статически определимых системах они не возникают). 6. Определим дополнительные усилия и напряжения в стержнях, возникающие при сборке из-за неточности изготовления стержня № 2. Длина стержня № 2 превышает номинальное значение на величину Уравнение равновесия статики аналогично (2.9). Уравнение перемещений получим с помощью геометрической картины перемещений (рис. 2.6, д):
где Следовательно,
Отсюда
или
В результате решения системы уравнений (2.9) и (2.11) получаем: N 1 = – 248,9 Н ≈ – 0,249 кН; N 2 = – 81,3 Н = – 0,0813 кН. Оба стержня сжаты. Соответствующие монтажные напряжения:
Действительные напряжения в стержнях, то есть напряжения от действующей нагрузки с учетом монтажных напряжений (см. п. 3):
(Наличие сборочных напряжений может существенно изменить значения напряжений в элементах статически неопределимой системы, вызванных действующей нагрузкой. В статически определимых системах монтажные напряжения не возникают). 7. Определим разрушающую нагрузку стержневой системы, считая материал стержней идеально упругопластическим (предел текучести Из расчета, сделанного по упругой стадии работы материала (см. пп. 1 – 3), следует, что стержень № 2 более нагружен, чем стержень № 1. Следовательно, если нагрузку увеличивать, то в стержне № 2 напряжения достигнут предела текучести в первую очередь. Дальнейшее увеличение нагрузки приведет к росту напряжений в сечениях стержня № 1 при постоянных напряжениях в сечениях стержня № 2, равных σT. При достижении напряжениями стержня № 1 предела текучести стержневая система перестает сопротивляться возрастанию нагрузки и превращается в механизм. Соответствующая этому состоянию системы (рис. 2.6, е) нагрузка является разрушающей. Из уравнения равновесия статики (2.4) имеем:
где
Тогда
Зависимость напряжений в стержнях от нагрузки Р показана на рис. 2.6, ж. При запасе прочности nT = 1,5, таком же, как в методе допускаемых напряжений (см. п. 2:
что превышает расчетную нагрузку (Р = 30 кН) на 12,9 %. Примечание (для студентов строительных специальностей): при решении задачи по п. 2 условия прочности по методу предельных состояний следует записывать в виде:
где R = 210 МПа – расчетное сопротивление материала стержней. При этом нагрузку Р в выражениях (2.8) считать расчетной.
Рекомендуемая литература
1. Феодосьев, В.И. Сопротивление материалов / В.И. Феодосьев. – М.: Наука, 1986. – С. 44-48. 2. Долинский, Ф.В. Краткий курс сопротивления материалов / Ф.В. Долинский, М.Н. Михайлов. – М.: Высшая школа, 1988. – 3. Смирнов, А.Ф. Сопротивление материалов / А.Ф. Смирнов, А.В. Александров, Н.И. Монахов и др. – М.: Высшая школа, 1975. – 4. Александров, А.В. Сборник задач по сопротивлению материалов / А.В. Александров, Б.П. Державин, Б.Я. Лащеников и др. – М.: Стройиздат, 1977. – С. 15-26; 30-37. 5. Кобяков, Е.Т. Задания и методические указания к расчетно-проектировочной работе № 2 по сопротивлению материалов. Расчет статически неопределимых систем при растяжении и сжатии /
|


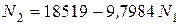 . (2.10)
. (2.10)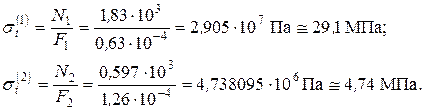
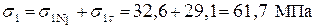 (растяжение).
(растяжение). (сжатие).
(сжатие). .
. ,
,
 .
.
 . (2.11)
. (2.11)
 (растяжение);
(растяжение); (сжатие).
(сжатие). ,
,

 .
. ), допускаемая нагрузка, найденная по методу разрушающих нагрузок, равна:
), допускаемая нагрузка, найденная по методу разрушающих нагрузок, равна: