Пример решения задачи № 2. Требуется определить главные центральные моменты инерции несимметричного сечения, составленного из прокатных профилей (рис
Требуется определить главные центральные моменты инерции несимметричного сечения, составленного из прокатных профилей
Размеры в см

Рисунок 4.6 – Сечение к задаче № 2 Решение: по размерам, взятым из таблиц (ГОСТ 8240-72 и 1. Определение центра тяжести сечения. В соответствии с присвоенными элементам сечения номерами Площади сечений швеллера и уголка даны в таблицах стандартов: F 1 = 10,90 см2; F 2 = 3,17 см2. Площадь всего сечения:
Определим положение центра тяжести заданного сечения в системе координат C1х1у1 по формулам (4.1):
Показываем центр тяжести сечения на чертеже (т. С). (Если координаты х1c и у1c найдены верно, то точка С должна лежать на прямой между точками C1, C2). Через центр тяжести сечения (т. С) проводим оси x0, y0 и указываем расстояния между осями x0 и x1, y0 и y1 (см. рис. 4.6). 2. Определение осевых и центробежного моментов инерции се-чения. Выписываем из таблиц стандартов необходимые значения моментов инерции элементов сечения относительно указанных на чертеже (см. рис. 4.6) осей:
Ось u2 для уголка есть ось минимального момента инерции. Она наклонена к центральной оси, параллельной длинной полке, под углом α;2 (согласно ГОСТ 8510-72, tg α;2 = 0,401) и пересекает обе полки уголка. В данном случае
Вторая главная центральная ось уголка (v2) перпендикулярна к оси u2. Для этой оси
Центробежный момент инерции уголка относительно его центральных осей x2, y2 (см. рис. 4.6):
Это значение может быть проверено по формуле
Для швеллера оси x1, y1 являются главными центральными, так как ось х1 есть ось симметрии. Поэтому По формулам (4.3) и (4.4) вычисляем осевые и центробежный моменты инерции заданного сечения относительно центральных
3. Определение положения главных центральных осей и вычисление значений главных центральных моментов инерции сечения.
Следовательно,
Так как Вычисляем значения главных центральных моментов инерции сечения:
Проверяем правильность определения величин Iu, Iv:
Главные центральные оси u (min) и v (max) проведены на чертеже сечения (см. рис. 4.6).
|


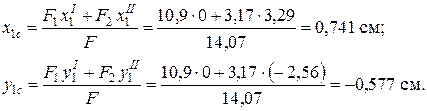
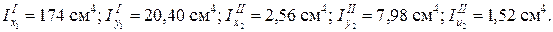
 .
. .
.

 .
.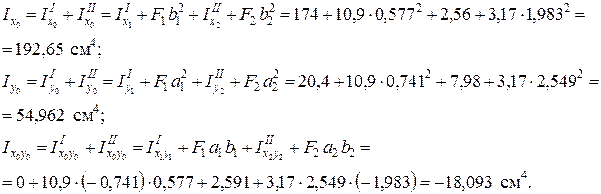
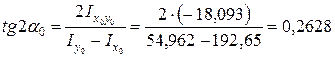 .
.
 , оси x0, y0 для получения направлений главных центральных осей заданного сечения следует повернуть против хода часовой стрелки.
, оси x0, y0 для получения направлений главных центральных осей заданного сечения следует повернуть против хода часовой стрелки.






