Краткие теоретические сведения. В результате действия приложенной нагрузки первоначально прямолинейная ось балки искривляется
В результате действия приложенной нагрузки первоначально прямолинейная ось балки искривляется. Изогнутую ось балки называют упругой линией. Если упругая линия есть плоская кривая, лежащая в плоскости нагрузки, изгиб называют прямым или плоским. Для того чтобы изгиб был прямым, достаточно, чтобы плоскость нагружения совпадала с одной из главных центральных плоскостей балки, являющейся ее плоскостью симметрии. Если сечение балки не имеет оси симметрии, плоскость нагружения должна проходить по ее главной плоскости, содержащей ось центров изгиба [1]. В противном случае балка будет испытывать косой изгиб в сочетании с кручением. В дальнейшем будем предполагать, что условие возникновения прямого изгиба выполнено. Во многих случаях такие распространенные элементы машиностроительных и строительных конструкций, как балки, должны быть рассчитаны не только на прочность по наибольшим нормальным напряжениям, а в некоторых случаях и по касательным и главным напряжениям, но и на жесткость. Расчет на жесткость проводится с той целью, чтобы не допустить чрезмерно больших упругих перемещений поперечных сечений балки, которые могут привести к нарушению нормальных условий работы конструкции. Это одна из важнейших задач инженерной практики, решаемая методами сопротивления материалов. При прямом изгибе балки центры тяжести ее поперечных сечений перемещаются в плоскости нагружения. На рис. 5.1, а показана ось балки, заделанной одним концом (консоль), до и после нагружения силой Р.
аб
Рисунок 5.1 – Перемещения при изгибе балки
Точка К оси балки, заданная координатой z, в результате деформации балки переместилась в точку Можно показать, что горизонтальные перемещения w в балках большой жесткости являются малыми величинами второго порядка малости в сравнении с вертикальными перемещениями v [2, 3]. Поэтому величиной w в этих случаях пренебрегают. Это равносильно допущению, что центры тяжести поперечных сечений перемещаются в направлениях, перпендикулярных к недеформированной оси балки (см. рис. 5.1, б). Эти перемещения называют прогибами. Условимся считать прогибы положительными при перемещении сечения вдоль оси Оу вверх (см. рис. 5.1). В дальнейшем принимаем v(z) = y(z). Искривление оси балки при ее деформации в случае поперечного изгиба сопровождается искривлениями плоскостей поперечных сечений, то есть сечения не остаются плоскими в отличие от чистого Поэтому под углом поворота j сечения балки при поперечном изгибе понимают угол между нормалями, проведенными в плоскости изгиба в соответствующих точках (К и К' – см. рис. 5.1, б) к оси балки до и после ее деформации. Причем, как следует из рисунка 5.1, б, угол поворота поперечного сечения j равен углу наклона θ к оси Oz касательной, проведенной к упругой линии в точке К, то есть j = θ. Согласно геометрическому смыслу производной, рассматривая упругую линию балки как кривую в системе осей координат Оуz, имеем: y'(z) = tg θ.
Но при малых прогибах tg θ ≈ θ ≈ j, поэтому
j (z) = y'(z), (5.1) где угол j, являющийся функцией координаты z, выражен в радианах. Знак угла j совпадает в системе осей Оуz со знаком первой производной от функции прогибов y'(z), то есть угол поворота сечения положителен при повороте сечения против хода часовой стрелки. Условие жесткости балки выражает требование, согласно которому ее наибольший прогиб vmax, выраженный в долях пролета ℓ, не должен превышать допускаемого значения 1/n:
где 1/n в зависимости от назначения балки устанавливается нормами проектирования. Для стальных балок 1/n = 1/200 ÷ 1/1000, например, для железнодорожных мостов 1/n ≈ 1/1000. Эти значения показывают малость прогибов балки в сравнении с длиной ℓ ее пролета, что и дает возможность принять указанные упрощающие допущения. Для определения прогибов применяются различные методы, некоторые из которых рассмотрены ниже.
|
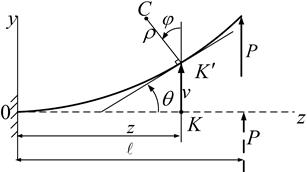
. Ее полное перемещение разложено на вертикальную v и горизонтальную w составляющие.
(5.2)
