Пример расчета балки к заданию
Для балки двутаврового поперечного сечения (рис. 5.8, а) требуется: 1) подобрать номер двутавра по условию прочности при изгибе, приняв [s] = 160 МПа (R = 200 MПа); 2) проверить прочность балки по наибольшим касательным напряжениям, возникающим в поперечных сечениях, приняв [τ] = 100 МПа (Rс = 110 МПа); 3) построить упругую линию и проверить балку на жесткость, если допускаемый прогиб [v] = (1/250)∙ℓ, где ℓ – длина пролета. Модуль упругости материала Е = 2∙105 МПа. (Данные в скобках – для студентов строительных специаль-ностей).


Рисунок 5.8 – Расчетная схема балки и эпюры Qy, Мx, v
Решение: определяем реакции опор балки из уравнений равновесия статики:
Проверка:
Пользуясь методом сечений, построим эпюры поперечных сил Qy и изгибающих моментов Мx. Разбивку балки на участки I, II, III, IV производим слева направо. Составляем аналитические выражения поперечных сил по участкам:
Производим вычисления:
Эпюра Qy построена на рис. 5.8, б. Составляем аналитические выражения изгибающих моментов:
В результате вычислений находим:
По полученным данным строим эпюру Мx (рис. 5.8, в). Наибольшее значение изгибающего момента (Мx = 24,8 кНм) возникает в сечении балки у опоры В слева. Из условия прочности:
определим необходимое значение момента сопротивления Wx поперечного сечения:
Ближайшими номерами двутавра по ГОСТ 8239-72 являются № 18 (Wx = 143 см3, Jx = 1290 см4) и № 18а (Wx = 159 см3, Jx = 1430 см4). Проверим двутавр № 18, вычислив для него наибольшее напряжение:
Перенапряжение составляет:
что недопустимо, так как оно не должно превышать 5 %. Поэтому принимаем двутавр № 18а, в котором
Недонапряжение составляет 2,5 %. Наибольшее значение поперечной силы возникает в сечении у опоры А справа:
Определим наибольшие касательные напряжения в этом сечении по формуле Журавского:
где Для двутавра опасная по касательным напряжениям точка находится на нейтральной оси x, поэтому Следовательно,
Условие прочности по касательным напряжениям: τmax ≤ [τ], где согласно заданию [τ] = 100 МПа, удовлетворено. Балки из тонкостенных прокатных профилей следует проверять также на прочность по главным напряжениям, с применением теорий прочности, в сечениях, в которых изгибающий момент и поперечная сила одновременно достигают больших значений. В данном примере таким сечением является сечение левее точки С (Мx = 20,8 кНм и Однако, поскольку соответствующий учебный материал изучается во второй части курса, ограничимся лишь сделанным замечанием, цель которого – обратить внимание студента на необходимость проведения полной проверки прочности балок в указанном случае. Примеры расчетов изложены в [4]. Построение упругой линии балки выполним с помощью универсального уравнения упругой линии (5.8). При начале координат на левом конце балки (см. рис. 5.8) имеем:
Начальные параметры j 0 и y0 определим из граничных условий:
Упрощая систему уравнений, получим:
откуда Для данной балки жесткость сечения при изгибе
Поэтому Учитывая найденные значения j 0 и y0, составляем универсальное уравнение в окончательном виде:
Путем дифференцирования функции y(z) получаем уравнение углов поворота поперечных сечений:
Пользуясь составленными уравнениями, вычисляем прогибы и углы поворота ряда сечений. Результаты вычислений сводим в таб-
Таблица 5.2 – Прогибы и углы поворота поперечных сечений балки (рис. 5.8)
По полученным данным в принятом масштабе строим эпюру прогибов (см. рис. 5.8, г). На кривой y(z) имеются точки перегиба при значениях абсциссы z, при которых Mх = 0, что следует из формулы (5.3). Наибольший прогиб возникает в правом концевом сечении балки:
vmax = 3,22 мм.
Допускаемое значение прогиба согласно заданию составляет:
[v] = (1/250)∙1,6 = 6,4∙10–3 = 6,4 мм. Таким образом, условие жесткости v max ≤ [ v ] удовлетворено. Примечания: 1. При оформлении расчетной работы следует привести подробный расчет численных значений прогибов и углов поворота сечений, включенных в таблицу 5.2. 2. Студентам строительных специальностей при выполнении
|










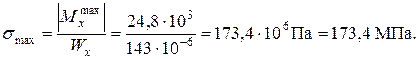




 – значение статического момента отсеченной части площади поперечного сечения относительно нейтральной оси x, соответствующее точке сечения, в которой определяются касательные напряжения; b – ширина поперечного сечения в этой точке.
– значение статического момента отсеченной части площади поперечного сечения относительно нейтральной оси x, соответствующее точке сечения, в которой определяются касательные напряжения; b – ширина поперечного сечения в этой точке.











