Необходимые сведения о расчетах на прочность
Расчетная формула для определения нормальных напряжений в произвольной точке поперечного сечения балки при изгибе имеет вид:
где Мх – изгибающий момент в сечении; у – координата рассматриваемой точки относительно нейтральной оси; Jx – осевой момент инерции сечения относительной этой оси. Наибольшие напряжения возникают в точках сечения, наиболее удаленных от нейтральной оси, то есть при Балки, материал которых одинаково сопротивляется растяжению и сжатию, проектируют так, чтобы их поперечное сечение было симметричным относительно нейтральной оси. В этом случае условие прочности по методу допускаемых напряжений записывают в виде:
где Для балок постоянного по длине сечения изгибающий момент Мх для расчета на прочность берется в опасном сечении, то есть принимают По условию прочности решают три типа задач: 1) задачи на проверку прочности (поверочный расчет); 2) задачи на определение допускаемой нагрузки; 3) задачи на подбор сечения (проектный расчет). В задании № 5 имеется в виду подбор сечения балки двутаврового сечения, для которой должно выполняться условие
Определив по этой формуле наименьшее допускаемое значение Wx, его округляют до ближайшего стандартного значения. При этом перенапряжение не должно превышать 5 % относительно допускаемого напряжения. Метод допускаемых напряжений до настоящего времени остается основным расчетным методом в машиностроении. При расчете и проектировании строительных конструкций пользуются методом предельных состояний. Расчет по первой группе предельных состояний (расчет по несущей способности) проводится по условию, которое в данном случае может быть представлено в виде:
где R – расчетное сопротивление материала; g – коэффициент условий работы (при нормальных условиях g = 1). По этой формуле также решают три типа задач, указанные выше. Балки, материал которых различно сопротивляется растяжению и сжатию, должны иметь поперечные сечения, несимметричные относительно нейтральной оси. Это вытекает из требования равной прочности растянутой и сжатой зон сечения. Для этих балок записывают два условия прочности – отдельно для растянутой и сжатой зон
где В некоторых случаях расчет на прочность по нормальным напряжениям является недостаточным, и дополнительно проводят расчет по главным напряжениям (с использованием гипотез прочности) и по наибольшим касательным напряжениям. Проверка на прочность по касательным напряжениям необходима в случаях коротких балок, деревянных балок, а также для балок из тонкостенных прокатных профилей, особенно вблизи опор, где часто возникают большие поперечные силы. Условие прочности по наибольшим касательным напряжениям, определяемым по формуле Д.И. Журавского, согласно методу допускаемых напряжений записывают в виде:
где Допускаемое напряжение на срез [ t ] принимают 0,5 ¸ 0,6 от [ s ]. При расчете по методу предельных состояний проверка прочности по наибольшим касательным напряжениям проводится по условию
где Rc – расчетное сопротивление материала на срез;
|
,
.
,
– осевой момент сопротивления сечения; 
– допускаемое напряжение.
.
.
,
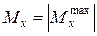и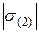 
– соответственно наибольшее растягивающее напряжение и наибольшее (по модулю) сжимающее напряжение; 
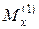и 
– взятые по абсолютному значению изгибающие моменты в опасных сечениях для зон растяжения и сжатия;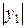 
и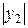 
– расстояния от нейтральной оси х до крайних точек сечений, в которых возникают наибольшие напряжения; 
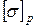и 
– допускаемые напряжения на растяжение и сжатие.
,
– значение наибольшей по абсолютному значению поперечной силы;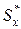 
– статический момент части сечения, соответствующий точке с наибольшим касательным напряжением, относительно нейтральной оси (в случае двутавра 
имеет место в точках сечения на нейтральной оси, а соответствующий статический момент полусечения имеется в таблице стандарта); b – ширина сечения в точке с наибольшим касательным напряжением (в случае двутавра – толщина его стенки).
,
