Пример решения задачи № 1
Вычерчиваем в масштабе расчетную схему балки по исходным данным (см. табл. 6.1) в соответствии с заданным вариантом Решение: определяем реакции опор из уравнений статики:
Проверка полученных значений реакций опор:
Найденные реакции опор указываем на расчетной схеме. Разбиваем балку на участки и составляем аналитические выражения внутренних силовых факторов по участкам: Участок I Участок II Участок III (0
Пользуясь полученными выражениями, строим эпюры поперечных сил

Рисунок 6.7 – Схема к расчету статически определимой балки
Проверив эпюры по известным правилам, определяем необходимое значение момента сопротивления сечения балки из условия прочности:
По таблице (ГОСТ 8239-72) выбираем двутавр № 16, для которого Определяем наибольшие касательные напряжения:
Условие прочности по касательным напряжениям: Определяем жесткость: Для определения прогиба балки в т. К прикладываем в этой точке в направлении искомого прогиба единичную силу и строим от нее эпюру изгибающих моментов Применяем способ Верещагина и определяем искомый прогиб. При этом делается разбивка (расслаивание) площади "грузовой" эпюры Умножая площади эпюры Мх на ординаты под их центрами тяжести на эпюре
Для определения угла поворота сечения А прикладываем к балке в этом сечении в направлении искомого угла единичный момент и строим эпюру изгибающих моментов М 2 (см. рис. 6.7, д). Применяя способ Верещагина, находим:
Положительные результаты вычислений означают, что перемещения происходят в направлениях приложенных единичных силовых факторов (силы и момента).
|



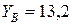 кН;
кН;

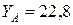 кН.
кН. :
:  .
. 0,4 м) (
0,4 м) ( 0,6 м) (
0,6 м) ( 0,5 м)
0,5 м) ;
;  ;
;  ;
; ;
; 
 .
. и изгибающих моментов
и изгибающих моментов  (рис. 6.7 б, в).
(рис. 6.7 б, в).



 .
. ,
,  ,
,  , d = 5 мм.
, d = 5 мм.
 [
[  ], где согласно заданию [
], где согласно заданию [  МНм2.
МНм2. (см. рис. 6.7, г).
(см. рис. 6.7, г). ) на плечо, то есть расстояние от линии действия силы до центра тяжести соответствующей части площади эпюры Мх. Ординаты указаны на “единичной” эпюре
) на плечо, то есть расстояние от линии действия силы до центра тяжести соответствующей части площади эпюры Мх. Ординаты указаны на “единичной” эпюре 




