Пример решения задачи № 4
Вычерчиваем расчетную схему неразрезной балки в масштабе, выбрав исходные данные из таблицы 6.4 (рис. 6.10, а). (Выписывается текст задания – см. п. 6.1). Решение: заданная балка один раз статически неопределима Полагая n = 1 (см. уравнение (6.1)), получаем:
Строим эпюру изгибающих моментов в основной системе от нагрузки в пролетах. (Эпюра строится для каждого пролета в отдельности только от нагрузки этого пролета, то есть так же, как это делается в статически определимых балках (рис. 6.10, в, г)). В данном случае
Подставив эти значения в уравнение трех моментов, получим:
откуда
Статическая неопределимость раскрыта. Переходим к построению окончательных эпюр Для левого пролета с консолью имеем:
      
Рисунок 6.10 – Схема к расчету неразрезной балки
Для правого пролета:
Необходимые построения показаны на схеме (рис. 6.10, д, е, ж). Сделаем деформационную проверку, перемножив по способу Верещагина эпюру
Из условия прочности на изгиб определим необходимое значение осевого момента сопротивления сечения балки:
По ГОСТ 8239-72 выбираем двутавр № 20a, для которого Определяем наибольшие касательные напряжения:
Условие прочности по касательным напряжениям: Вычисляем жесткость: Определим прогиб концевого сечения балки. Для этого эпюру
Аналогично определяем угол поворота сечения балки над опорой 1, перемножая эпюры
Сечение поворачивается по ходу часовой стрелки. Примечание: при составлении правой части уравнения трех моментов от более сложной нагрузки, чем показано на схеме (рис. 6.10), следует воспользоваться способом расслаивания эпюр или применить уравнение (6.2).
Рекомендуемая литература
1. Феодосьев, В.И. Сопротивление материалов / В.И. Феодосьев. – М.: Наука, 1986. – С. 189-250. 2. Смирнов, А.Ф. Сопротивление материалов / А.Ф. Смирнов, А.В. Александров, Н.И. Монахов и др. – М.: Высшая школа, 1975. – 3. Кобяков, Е.Т. Расчет неразрезных балок на действие статической нагрузки / Е.Т. Кобяков. – Орел: ОФ МИП, 1992. – 33 с. 4. Кобяков, Е.Т. Определение перемещений в статически определимых балках при прямом поперечном изгибе / Е.Т. Кобяков. – Орел: ОрелГПИ, 1994. – 34 с. 5. Александров, А.В. Сопротивление материалов / А.В. Александров, В.Д. Потапов, Б.П. Державин. – М.: Высшая школа, 1995. – С. 256-267. ЗАДАНИЕ № 7. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Цель и содержание задания
При проектировании инженерных сооружений, помимо расчетов на прочность, во многих случаях являются обязательными расчеты на устойчивость, так как в процессе эксплуатации потеря устойчивости упругой системой первоначальной (проектируемой) формы равновесия должна быть исключена. Целью выполнения задания является освоение практического метода решения одной из типовых задач расчетов на устойчивость сжатых стержней, заключающегося в подборе размеров сечения стержня из условия его устойчивости. Требуется рассчитать сжатый стержень (рис. 7.1), состоящий из сваренных между собой элементов (частей), обозначенных А и Б В середине (по длине) составного стержня в одной из его частей (А или Б) имеется сквозной вырез. Поэтому сжатый стержень в месте выреза необходимо проверить на прочность. Концентрацию напряжений не учитывать. Исходные данные согласно заданному варианту следует выбрать из таблицы 7.1.
Таблица 7.1 – Данные к заданию № 7
Рисунок 7.1 – Расчетные схемы сжатых стоек
Рисунок 7.2 – Типы сечений стоек
|

 в сечении над промежуточной опорой 1 (рис. 6.10, б).
в сечении над промежуточной опорой 1 (рис. 6.10, б). .
. ;
;  ;
;  м;
м;  м;
м;  ;
; ;
;  м.
м.

 и
и  для заданной балки. Для этого рассматриваем каждый пролет балки отдельно, находим реакции опор (с учетом момента
для заданной балки. Для этого рассматриваем каждый пролет балки отдельно, находим реакции опор (с учетом момента 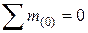 :
: 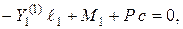
 ;
; :
: 
 кН;
кН; :
:  (проверка).
(проверка). кН;
кН;  кН;
кН;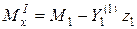 ;
;  (
( м;
м;  м).
м).
 кН;
кН; :
: 
 кН;
кН;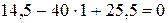 (проверка).
(проверка). ;
;  (
( ).
).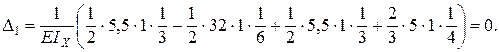
 ;
;  .
.
 ,
, 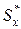 = 114 см3; d = 5,2 мм.
= 114 см3; d = 5,2 мм.
 , где
, где 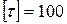 МПа, удовлетворено.
МПа, удовлетворено.
 перемножим с «единичной» эпюрой М 2, которую строим в основной системе от единичной силы, приложенной в т. К. (Основная система может выбираться различными способами. В данном случае для упрощения вычислений удобно воспользоваться основной системой, полученной путем разрезания балки над промежуточной опорой 1).
перемножим с «единичной» эпюрой М 2, которую строим в основной системе от единичной силы, приложенной в т. К. (Основная система может выбираться различными способами. В данном случае для упрощения вычислений удобно воспользоваться основной системой, полученной путем разрезания балки над промежуточной опорой 1).
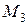 :
: .
. 16
16
 14
14
 12
12
 16
16
 12
12
















