Пример решения задачи № 3. Вычерчиваем в масштабе расчетную схему рамы по исходным данным, взятым из табл
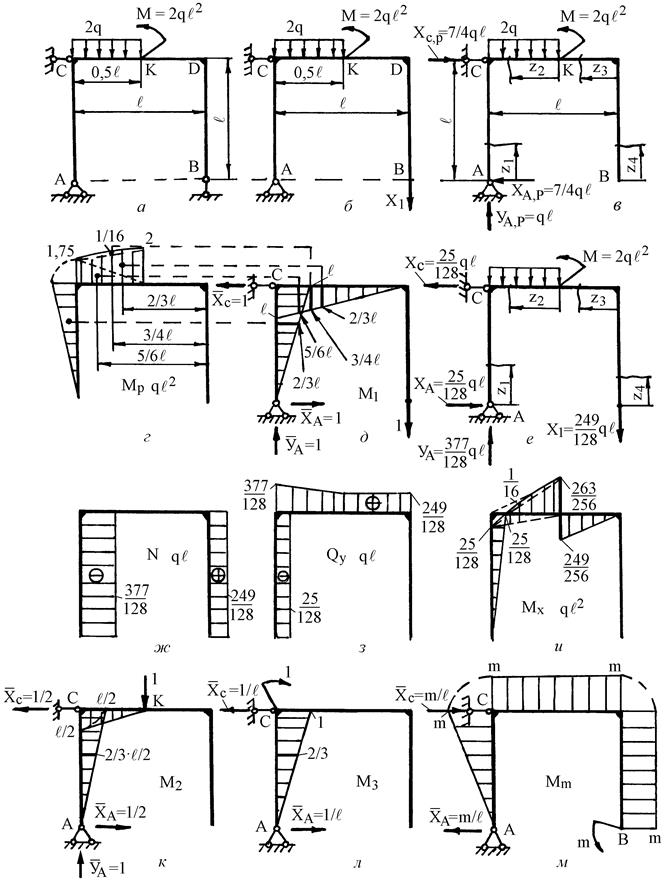
Вычерчиваем в масштабе расчетную схему рамы по исходным данным, взятым из табл. 6.3 (рис. 6.9, а). (Выписывается текст задания – см. п. 6.1). Решение: рама один раз статически неопределима (s = 1). Выбираем основную систему и прикладываем к ней заданную нагрузку, а взамен отброшенной связи указываем неизвестную реакцию Записываем каноническое уравнение метода сил:
Величины Умножая эпюру
Перемножением эпюр
Решив каноническое уравнение, имеем:
Статическая неопределимость раскрыта. Переходим к построению окончательных эпюр для заданной системы. Заново вычерчиваем схему (рис. 6.9, б) с указанием значений всех нагрузок и силы
Знак (–) означает, что реакция
Реакция Пользуясь схемой (рис. 6.9, е), составляем аналитические выражения внутренних силовых факторов и строим окончательные эпюры
Участок I Участок II Участок III Участок IV (
Сделаем деформационную проверку правильности расчета, перемножив эпюры
Чтобы определить вертикальное перемещение т. К, строим в основной системе эпюру изгибающих моментов от единичной силы, приложенной в т. К в заданном направлении, и эту эпюру перемножаем с эпюрой Мх (рис. 6.9, и, к):
Точка К перемещается вниз (в направлении единичной силы). Аналогично находим угол поворота узла С (рис. 6.9, и, л):
Узел С поворачивается по ходу часовой стрелки, то есть в направлении единичного момента. (В данном примере расчеты выполнены в обыкновенных дробях. Это дает возможность в результате деформационной проверки получить точный нуль. Если дроби окажутся громоздкими, следует перейти к десятичным дробям, округляя результаты с точностью до Для ответа на второй вопрос задания построим эпюру изгибающих моментов от внешнего момента m, приложенного в сечении В основной системы (рис. 6.9, м). Перемножив эту эпюру с эпюрой
Знак (–) указывает на то, что т. В перемещается вверх. Для того чтобы выполнялось условие
откуда, подставив найденные выражения перемещений, получим:
Знак (–) означает, что момент в сечении В следует приложить в направлении хода часовой стрелки.
|

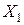 этой связи (рис. 6.9, б).
этой связи (рис. 6.9, б).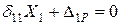 .
. и
и 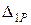 определим способом Верещагина. Для этого в основной системе строим эпюры изгибающих моментов от заданной нагрузки (рис. 6.9, в, г) и от единичной силы, приложенной по направлению неизвестной реакции
определим способом Верещагина. Для этого в основной системе строим эпюры изгибающих моментов от заданной нагрузки (рис. 6.9, в, г) и от единичной силы, приложенной по направлению неизвестной реакции 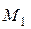 саму на себя, находим:
саму на себя, находим: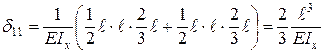 .
.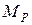 и
и  (см. рис. 6.9, г, д) получаем:
(см. рис. 6.9, г, д) получаем: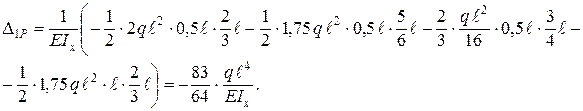
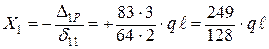 .
.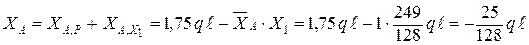 .
.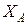 имеет направление, обратное направлению реакции
имеет направление, обратное направлению реакции 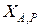 (от действующей нагрузки в основной системе), то есть направлена вправо:
(от действующей нагрузки в основной системе), то есть направлена вправо: ;
;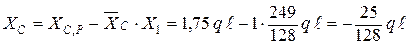 .
. противоположна направлению
противоположна направлению 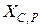 .
.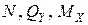 (рис. 6.9, ж, з, и):
(рис. 6.9, ж, з, и): ) (
) ( ) (
) (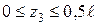 ) (
) (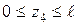 )
)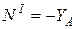 ;
; 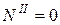 ;
; 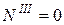 ;
; 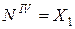 ;
;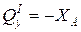 ;
; 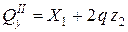 ;
; 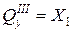 ;
; 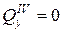 ;
;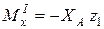 .
. 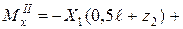
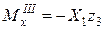 .
. 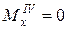 .
. .
. и
и 






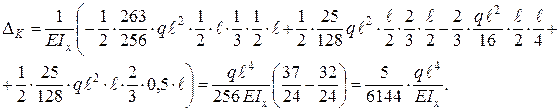

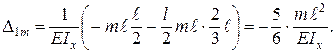
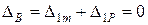 ,
,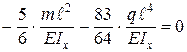 ;
;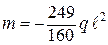 .
.


