Существует очень наглядный геометрический способ представления гармонических колебаний, заключающийся в изображении колебаний в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой (рис. 7.4).
Выберем ось  . Из точки О, взятой на этой оси, отложим вектор длины
. Из точки О, взятой на этой оси, отложим вектор длины  , образующий с осью угол
, образующий с осью угол  . Если привести этот вектор во вращение с угловой скоростью
. Если привести этот вектор во вращение с угловой скоростью  , то проекция конца вектора на ось
, то проекция конца вектора на ось  будет меняться со временем по закону
будет меняться со временем по закону  . Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора; с круговой частотой, равной угловой скорости вращения, и с начальной фазой, равной углу, образованному вектором с осью X в начальный момент времени.
. Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора; с круговой частотой, равной угловой скорости вращения, и с начальной фазой, равной углу, образованному вектором с осью X в начальный момент времени.
Векторная диаграмма дает возможность свести сложение колебаний к геометрическому суммированию векторов. Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты, которые имеют следующий вид:
 ,
, 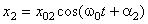 .
.
Представим оба колебания с помощью векторов  и
и  (рис. 7.5). Построим по правилу сложения векторов результирующий вектор
(рис. 7.5). Построим по правилу сложения векторов результирующий вектор  . Легко увидеть, что проекция этого вектора на ось
. Легко увидеть, что проекция этого вектора на ось  равна сумме проекций слагаемых векторов
равна сумме проекций слагаемых векторов  . Следовательно, вектор
. Следовательно, вектор  представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью
представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью  , что и векторы
, что и векторы  ,
,  , так что результирующее движение будет гармоническим колебанием с частотой
, так что результирующее движение будет гармоническим колебанием с частотой  , амплитудой
, амплитудой  и начальной фазой
и начальной фазой  . По теореме косинусов квадрат амплитуды результирующего колебания будет равен
. По теореме косинусов квадрат амплитуды результирующего колебания будет равен
| |  . .
| (7.3)
|
Из рис. 7.5 видно, что начальная фаза результирующего колебания будет равна
| |  . .
| (7.4)
|
Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения векторов. Формулы (7.3) и (7.4) можно, конечно, получить, сложив выражения для  и
и  аналитически, но метод векторной диаграммы отличается большей простотой и наглядностью.
аналитически, но метод векторной диаграммы отличается большей простотой и наглядностью.


 . Из точки О, взятой на этой оси, отложим вектор длины
. Из точки О, взятой на этой оси, отложим вектор длины  , образующий с осью угол
, образующий с осью угол  . Если привести этот вектор во вращение с угловой скоростью
. Если привести этот вектор во вращение с угловой скоростью  , то проекция конца вектора на ось
, то проекция конца вектора на ось  . Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора; с круговой частотой, равной угловой скорости вращения, и с начальной фазой, равной углу, образованному вектором с осью X в начальный момент времени.
. Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора; с круговой частотой, равной угловой скорости вращения, и с начальной фазой, равной углу, образованному вектором с осью X в начальный момент времени.
 ,
, 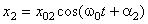 .
. и
и  (рис. 7.5). Построим по правилу сложения векторов результирующий вектор
(рис. 7.5). Построим по правилу сложения векторов результирующий вектор  . Легко увидеть, что проекция этого вектора на ось
. Легко увидеть, что проекция этого вектора на ось  равна сумме проекций слагаемых векторов
равна сумме проекций слагаемых векторов  . Следовательно, вектор
. Следовательно, вектор  представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью
представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью  , что и векторы
, что и векторы  ,
,  и начальной фазой
и начальной фазой  .
.
 .
.
 и
и  аналитически, но метод векторной диаграммы отличается большей простотой и наглядностью.
аналитически, но метод векторной диаграммы отличается большей простотой и наглядностью.


