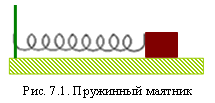
Говоря о колебаниях тела в механике, мы подразумеваем повторяющееся движение по одной и той же траектории. Простейшим примером периодического движения служат колебания груза на конце пружины (пружинный маятник) (рис. 7.1).
Если сдвинуть груз вправо, растягивая пружину, или влево, сжимая ее, то пружина действует на груз с силой, которая стремится вернуть его в положение равновесия; такую силу называют возвращающей. Для нашей системы возвращающая сила прямо пропорциональна расстоянию х, на которое сжимается или растягивается пружина ( ). Эта сила сообщает грузу ускорение, и груз приходит в положение равновесия. В положении равновесия сила, действующая на груз, уменьшается до нуля, а скорость его в этой точке максимальна. Возвратившись в устойчивое состояние, колебательная система не может сразу остановиться. В механических колебательных системах этому мешает инертность колеблющегося тела. Поэтому груз пройдет положение равновесия и будет двигаться далее, что приведет к сжатию пружины. Сила со стороны пружины в результате ее сжатия замедляет движение груза, и в некоторой точке его скорость будет равна нулю. Затем груз начинает двигаться в противоположном направлении и приходит в точку, откуда он начал движение. Затем весь этот процесс повторяется. Пружина, груз – пример колебательной системы. Расстояние х груза от положения равновесия до точки, в которой в данный момент времени находится груз, называют смещением.
). Эта сила сообщает грузу ускорение, и груз приходит в положение равновесия. В положении равновесия сила, действующая на груз, уменьшается до нуля, а скорость его в этой точке максимальна. Возвратившись в устойчивое состояние, колебательная система не может сразу остановиться. В механических колебательных системах этому мешает инертность колеблющегося тела. Поэтому груз пройдет положение равновесия и будет двигаться далее, что приведет к сжатию пружины. Сила со стороны пружины в результате ее сжатия замедляет движение груза, и в некоторой точке его скорость будет равна нулю. Затем груз начинает двигаться в противоположном направлении и приходит в точку, откуда он начал движение. Затем весь этот процесс повторяется. Пружина, груз – пример колебательной системы. Расстояние х груза от положения равновесия до точки, в которой в данный момент времени находится груз, называют смещением.
Любая колебательная система, в которой возвращающая сила прямо пропорциональна смещению, взятому с противоположным знаком (например, упругая сила  ), совершает гармонические колебания. Такую силу называют квазиупругой, а саму систему часто называют гармоническим осциллятором.
), совершает гармонические колебания. Такую силу называют квазиупругой, а саму систему часто называют гармоническим осциллятором.
Рассмотрим уравнение, описывающее колебания, совершаемые системой в направлении оси X в отсутствие сил трения. Для этого воспользуемся вторым законом Ньютона 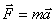 . Ускорение
. Ускорение 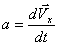 , а так как
, а так как  , то ускорение можно получить, если два раза взять производную от координаты по времени. Тогда
, то ускорение можно получить, если два раза взять производную от координаты по времени. Тогда  . Так в математике обозначается вторая производная. Теперь уравнение движения осциллятора можно записать в виде:
. Так в математике обозначается вторая производная. Теперь уравнение движения осциллятора можно записать в виде:
 .
.
Введем обозначение 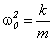 , тогда уравнение запишется в следующем виде:
, тогда уравнение запишется в следующем виде:
 ,
,
здесь  – ускорение движущейся точки.
– ускорение движущейся точки.
Поскольку  ,
,  – величина, зависящая от свойств системы, совершающей колебания. Решение этого уравнения имеет вид:
– величина, зависящая от свойств системы, совершающей колебания. Решение этого уравнения имеет вид:
| | 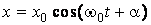
| (7.1)
|
где  и
и  – произвольные постоянные, которые определяются из начальных условий. В качестве таковых можно, например, взять значение отклонения
– произвольные постоянные, которые определяются из начальных условий. В качестве таковых можно, например, взять значение отклонения  и скорости
и скорости  в момент времени
в момент времени  . В справедливости (7.1) можно убедиться на простом опыте. Если к колеблющемуся грузу прикрепить карандаш и протягивать под ним с постоянной скоростью лист бумаги, то карандаш вычертит синусоиду.
. В справедливости (7.1) можно убедиться на простом опыте. Если к колеблющемуся грузу прикрепить карандаш и протягивать под ним с постоянной скоростью лист бумаги, то карандаш вычертит синусоиду.
Таким образом, смещение  изменяется со временем по закону косинуса или синуса. Движение механической системы, находящейся под действием квазиупругой силы, представляет собой гармоническое движение.
изменяется со временем по закону косинуса или синуса. Движение механической системы, находящейся под действием квазиупругой силы, представляет собой гармоническое движение.
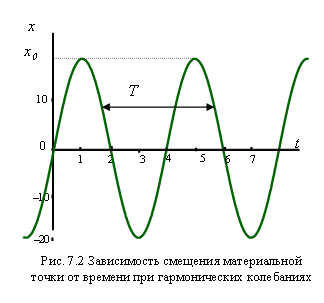
На рис. 7.2 приведен график зависимости смещения частицы от времени. По горизонтальной оси отложено время 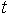 , по вертикальной – смещение x. Так как косинус изменяется от -1 до +1, значения
, по вертикальной – смещение x. Так как косинус изменяется от -1 до +1, значения  лежат в пределах от
лежат в пределах от  до
до  . Величина наибольшего отклонения системы от положения равновесия называется амплитудой колебания. Амплитуда
. Величина наибольшего отклонения системы от положения равновесия называется амплитудой колебания. Амплитуда  – постоянная положительная величина. Величина
– постоянная положительная величина. Величина  , стоящая под знаком косинуса, называется фазой колебания. Постоянная
, стоящая под знаком косинуса, называется фазой колебания. Постоянная  представляет собой значение фазы в момент
представляет собой значение фазы в момент  и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета времени.
и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета времени.
Поскольку косинус – периодическая функция с периодом  , различные состояния частицы, совершающей гармонические колебания, повторяются через такой промежуток времени T, за который фаза колебания получает приращение
, различные состояния частицы, совершающей гармонические колебания, повторяются через такой промежуток времени T, за который фаза колебания получает приращение  . Этот промежуток времени называется периодом колебания. Его можно определить из условия:
. Этот промежуток времени называется периодом колебания. Его можно определить из условия:
 ,
,
отсюда
 .
.
Число колебаний в единицу времени называется частотой колебаний. Очевидно, что частота связана с периодом колебаний соотношением
 .
.
Из определения периода следует, что  . Величину
. Величину  называют круговой или циклической частотой. Так как она зависит от свойств самой колеблющейся системы, то ее часто называют собственной частотой колебаний системы.
называют круговой или циклической частотой. Так как она зависит от свойств самой колеблющейся системы, то ее часто называют собственной частотой колебаний системы.
Примером системы, совершающей гармонические колебания, является математический маятник. Математический маятник – это тело, подвешенное на невесомой и нерастяжимой нити, находящееся в поле тяжести Земли. Математический маятник представляет идеализированную модель, правильно описывающую реальный маятник лишь при определенных условиях. Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного на ней тела, масса нити ничтожна мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь.
Колебательную систему в данном случае образуют нить, присоединенное к ней тело и Земля, без которой эта система не могла бы служить маятником. При колебаниях математического маятника периодически изменяется угол отклонения маятника от положения равновесия. Период свободных гармонических колебаний математического маятника равен
 ,
,
где  – длина нити, g – ускорение свободного падения. Таким образом, период свободных колебаний математического маятника не зависит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник.
– длина нити, g – ускорение свободного падения. Таким образом, период свободных колебаний математического маятника не зависит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник.

 ). Эта сила сообщает грузу ускорение, и груз приходит в положение равновесия. В положении равновесия сила, действующая на груз, уменьшается до нуля, а скорость его в этой точке максимальна. Возвратившись в устойчивое состояние, колебательная система не может сразу остановиться. В механических колебательных системах этому мешает инертность колеблющегося тела. Поэтому груз пройдет положение равновесия и будет двигаться далее, что приведет к сжатию пружины. Сила со стороны пружины в результате ее сжатия замедляет движение груза, и в некоторой точке его скорость будет равна нулю. Затем груз начинает двигаться в противоположном направлении и приходит в точку, откуда он начал движение. Затем весь этот процесс повторяется. Пружина, груз – пример колебательной системы. Расстояние х груза от положения равновесия до точки, в которой в данный момент времени находится груз, называют смещением.
). Эта сила сообщает грузу ускорение, и груз приходит в положение равновесия. В положении равновесия сила, действующая на груз, уменьшается до нуля, а скорость его в этой точке максимальна. Возвратившись в устойчивое состояние, колебательная система не может сразу остановиться. В механических колебательных системах этому мешает инертность колеблющегося тела. Поэтому груз пройдет положение равновесия и будет двигаться далее, что приведет к сжатию пружины. Сила со стороны пружины в результате ее сжатия замедляет движение груза, и в некоторой точке его скорость будет равна нулю. Затем груз начинает двигаться в противоположном направлении и приходит в точку, откуда он начал движение. Затем весь этот процесс повторяется. Пружина, груз – пример колебательной системы. Расстояние х груза от положения равновесия до точки, в которой в данный момент времени находится груз, называют смещением.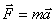 . Ускорение
. Ускорение 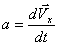 , а так как
, а так как  , то ускорение можно получить, если два раза взять производную от координаты по времени. Тогда
, то ускорение можно получить, если два раза взять производную от координаты по времени. Тогда  . Так в математике обозначается вторая производная. Теперь уравнение движения осциллятора можно записать в виде:
. Так в математике обозначается вторая производная. Теперь уравнение движения осциллятора можно записать в виде: .
.
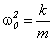 , тогда уравнение запишется в следующем виде:
, тогда уравнение запишется в следующем виде: ,
, – ускорение движущейся точки.
– ускорение движущейся точки. ,
,  – величина, зависящая от свойств системы, совершающей колебания. Решение этого уравнения имеет вид:
– величина, зависящая от свойств системы, совершающей колебания. Решение этого уравнения имеет вид: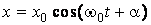
 и
и  – произвольные постоянные, которые определяются из начальных условий. В качестве таковых можно, например, взять значение отклонения
– произвольные постоянные, которые определяются из начальных условий. В качестве таковых можно, например, взять значение отклонения  и скорости
и скорости  в момент времени
в момент времени  . В справедливости (7.1) можно убедиться на простом опыте. Если к колеблющемуся грузу прикрепить карандаш и протягивать под ним с постоянной скоростью лист бумаги, то карандаш вычертит синусоиду.
. В справедливости (7.1) можно убедиться на простом опыте. Если к колеблющемуся грузу прикрепить карандаш и протягивать под ним с постоянной скоростью лист бумаги, то карандаш вычертит синусоиду. , по вертикальной – смещение x. Так как косинус изменяется от -1 до +1, значения
, по вертикальной – смещение x. Так как косинус изменяется от -1 до +1, значения  лежат в пределах от
лежат в пределах от  до
до  . Величина наибольшего отклонения системы от положения равновесия называется амплитудой колебания. Амплитуда
. Величина наибольшего отклонения системы от положения равновесия называется амплитудой колебания. Амплитуда  , стоящая под знаком косинуса, называется фазой колебания. Постоянная
, стоящая под знаком косинуса, называется фазой колебания. Постоянная  , различные состояния частицы, совершающей гармонические колебания, повторяются через такой промежуток времени T, за который фаза колебания получает приращение
, различные состояния частицы, совершающей гармонические колебания, повторяются через такой промежуток времени T, за который фаза колебания получает приращение  ,
, .
. .
. . Величину
. Величину  называют круговой или циклической частотой. Так как она зависит от свойств самой колеблющейся системы, то ее часто называют собственной частотой колебаний системы.
называют круговой или циклической частотой. Так как она зависит от свойств самой колеблющейся системы, то ее часто называют собственной частотой колебаний системы. ,
, – длина нити, g – ускорение свободного падения. Таким образом, период свободных колебаний математического маятника не зависит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник.
– длина нити, g – ускорение свободного падения. Таким образом, период свободных колебаний математического маятника не зависит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник.


