Принцип метода измерения и рабочая формула. Стеклянная призма является диспергирующей системой: она разлагает исследуемый свет в спектр по длинам волн
Стеклянная призма является диспергирующей системой: она разлагает исследуемый свет в спектр по длинам волн, что широко используется в различных спектральных приборах. Это свойство призмы обусловлено тем, что показатель преломления n стекла, из которого изготовлена призма, зависит от длины волны света l, поэтому свет разных длин волн, проходя через призму, отклоняется на разные углы. Для определения зависимости n (l) в случае призмы можно использовать метод, основанный на измерении угла наименьшего отклонения. Суть этого метода состоит в следующем. Пусть луч света с длиной волны l падает на грань призмы с преломляющим углом q под некоторым углом b (рис. 2). В результате двух преломлений на двух гранях призмы вышедший из нее луч отклоняется на угол a по отношению к падающему лучу. Угол a зависит от угла падения b, преломляющего угла призмы q, а также сорта стекла и длины волны света l. Можно показать, что при симметричном прохождении света через призмы (как на рис. 2) угол отклонения минимален. В этом случае показатель преломления и обозначим его, как aмин., определяется формулой
где угол aмин. зависит от l. В данной работе используется призма с q = 60о, и формула (1) упрощается:
Таким образом, определение показателя преломления для каждой длины волны сводится к измерению соответствующего угла наименьшего отклонения.
Рис. 2
|

 , (1)
, (1)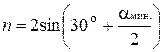 . (2)
. (2)



