Теоретические сведения. Для произвольно заданных узлов интерполирования пользуются формулой, обычно называемой интерполяционной формулой Лагранжа.
Для произвольно заданных узлов интерполирования пользуются формулой, обычно называемой интерполяционной формулой Лагранжа. Пусть на отрезке [a,b] заданы точки xk, k=0,1,…,n (узлы интерполирования), в которых известны значения функции f(x). Задача интерполирования алгебраическими многочленами состоит в том, чтобы построить многочлен степени n
значения которого в заданных точках совпадают со значениями функции f(x) в этих точках:
Для любой непрерывной функции f(x) сформулированная задача имеет единственное решение. Действительно, для отыскания коэффициентов a0,a1,…,anполучаем систему линейных уравнений
определитель которой (определитель Вандермонда) отличен от нуля, если среди точек xi, i=0,1,…,nнет совпадающих. Решение системы можно записать различным образом. Интерполяционный многочлен, представленный в виде
называется интерполяционным многочленом Лaгранжа (Жозеф Луи Лагранж — французский математик). Функции wi есть многочлены степени n, которые называются лагранжевыми коэффициентами:
Рассмотрим два частных случая интерполяционного полинома Лагранжа. 1. При
где 2. При
где
Отметим преимущества и недостатки многочлена Лагранжа. Преимущества: интерполяционный многочлен Лагранжа работает как для таблиц с постоянным шагом, так и для таблиц с переменным шагом; рni(x) не зависит от функции f(x), откуда следует, что по одной системе узлов можно интерполировать несколько функций. Недостатки: все слагаемые в формуле Лагранжа равнозначны, поэтому при добавление узлов таблицы многочлен Лагранжа придется полностью перестраивать. Погрешность интерполяционной формулы Лагранжа
где Величину ошибки можно минимизировать, если в качестве узлов интерполяции выбрать абциссы (узпы) полинома Чебышева. Многочлен Чебышева Tn(x) на интервале [-1,1] имеет ровно n действительных корней, определяемых как
|

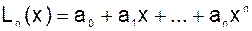 , (6.1)
, (6.1)
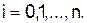 (6.2)
(6.2)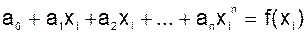 ,
, 
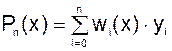 (6.3)
(6.3) (6.4)
(6.4)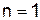 имеем две узловые точки. Формула Лагранжа представляет в этом случае уравнение прямой
имеем две узловые точки. Формула Лагранжа представляет в этом случае уравнение прямой  , проходящей через две заданные точки:
, проходящей через две заданные точки: ,
,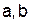 — абсциссы этих точек.
— абсциссы этих точек. получим уравнение параболы
получим уравнение параболы  , проходящей через три точки:
, проходящей через три точки:
 ,
,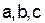 — абсциссы данных точек.
— абсциссы данных точек. удовлетворяет неравенству
удовлетворяет неравенству ,
, ,
,  ,
,  .
. . Для того чтобы решить задачу интерполяции на интервале [a,b], необходимо выполнить линейное преобразование
. Для того чтобы решить задачу интерполяции на интервале [a,b], необходимо выполнить линейное преобразование  .
.


