Пример построения полинома Лагранжа в пакете MATLAB.
function yy=lagrange(x,y,xx)
% число узлов интерполяции
N=length(x);
% число узлов, в которых высчитывается значение интерполяционного полинома
N_res=length(xx);
% создание нулевого массива значений интерполяционного полинома
yy=zeros(size(xx));
for k=1:N
% вычисление функции Лагранжа Li(X)
Li=ones(size(xx));
for j=[1:k-1, k+1:N]
for i=[1:N_res]
Li(i)=Li(i).*(xx(i)-x(j))/(x(k)-x(j));
end
end
% накопление суммы
yy = yy + y(k)*Li;
yy
end
Пример использования узлов Чебышева.
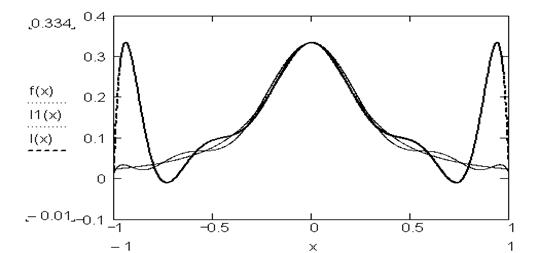
Заданная функция f(x) табулируется на интервале [-1,1] двумя способами: с шагом 0.2 и в узлах Чебышева. На двух полученных сетках строятся полиномы Лагранжа. Результаты визуализируются с помощью графиков. На графике, приведенном ниже, видно значительное отклонение полинома Лагранжа, построенного на сетке с шагом 0.2, от исходной функции и более приемлемое приближение функции для полинома, построенного на узлах Чебышева:
Узлы Чебышева:
Пример вычисления погрешности интерполирования.
Анализ погрешности замены исходной функции интерполяционным многочленом для таблиц с постоянным шагом:
Варианты лабораторных работ
| Номер
варианта
| Исходные данные
| |
| x
f(x)
| 1,4
0,3365
| 1,8
0.5878
| 2,3
0.8329
| 2,9
1.0647
| |
| x
f(x)
| 2,0
0,6931
| 2,5
0.9163
| 2,8
1.029б
| 3,3
1,1939
| |
| x
f(x)
| 4,0
1,3863
| 4,5
1,5041
| 4,9
1.5892
| 5,4
1.6864
| |
| x
f(x)
| 1,2
0,1823
| 1,6
0,4700
| 2,1
0.7419
| 2,6
1,6864
| |
| x
f(x)
| 2,2
0,7885
| 2,7
0,9933
| 3,1
1.1314
| 3,6
1,2809
| | | | | | | | |
Варианты лабораторных работ (продолжение)
| Номер
варианта
| Исходные данные
| | |
| x
f(x)
| 3,2
1,1632
| 3,6
1.2809
| 4,1
1,4110
| 4,6
1.5261
| | |
| x
f(x)
| 3,4
1,2238
| 3,9
1,3610
| 4.3
1,4586
| 4,9
1.5861
| | |
| x
f(x)
| 1,6
0,4700
| 2,1
0,7419
| 2,7
0,9933
| 8,2
1,1632
| | |
| x
f(x)
| 2,8
1,0296
| 3,1
1.1314
| 3,7
1,3083
| 4,2
1,4351
| | |
| x
f(x)
| 3,1
1,1314
| 3,6
1,2809
| 4,0
1,З863
| 4,6
1,5261
| | |
| x
f(x)
| 1,9
0,6419
| 2,5
0,9163
| 2,9
1,0647
| 3.4
1.2238
| | |
| x
f(x)
| 1,7
0,5306
| 2,2
0,7885
| 2,8
1.0296
| 3,2
1.1632
| | |
| x
f(x)
| 3,6
1.2809
| 4,2
1.4351
| 4,5
1,5041
| 5.2
1.6094
| | |
| x
f(x)
| 2,5
0,9163
| 2,9
1,0647
| 3,6
1.2809
| 4,1
1.4110
| | |
| x
f(x)
| 3,3
1,1939
| 3,9
1,3610
| 4,4
1,4816
| 5,0
1,6094
| |
| x
f(x)
| 1,1
0,0953
| 1,7
0,5306
| 2,4
0.6755
| 2,8
1,0296
| |
| x
f(x)
| 2,1
0.7419
| 2.5
0.9163
| 3,0
1,0986
| 3,5
1,2528
| |
| x
f(x)
| 3,2
1,1632
| 3,7
1.3083
| 4,3
1,4586
| 4,9
1,5892
| |
| x
f(x)
| 2,7
0.9933
| 3,3
1.1939
| 3,8
1.3350
| 4,6
1,5261
| |
| x
f(x)
| 1,0
0,0000
| 1,5
0.4055
| 2,1
0,7419
| 2,7
0.9933
| |
| x
f(x)
| 1,4
0,3365
| 1.9
0,6419
| 2,6
0,9555
| 3,0
1,0986
| |
| x
f(x)
| 3,1
1.1314
| 3.7
1,3083
| 4,2
1.4351
| 4.8
1.5686
| |
| x
f(x)
| 2,6
0.9555
| 3,2
1.1632
| 4.0
1.3863
| 4,5
1.5041
| |
| x
f(x)
| 1,6
0.4700
| 2,2
0,7885
| 2,7
.9933
| 8,4
1,2238
| |
| x
f(x)
| 2,1
0,7419
| 2,7
0,9933
| 3,3
1.1939
| 3,8
1.3350
| | | | | | | | | | | | |
Варианты лабораторных работ (окончание)
| Номер
варианта
| Исходные данные
| | |
| x
f(x)
| 2,6
0,9555
| 3.0
1,0986
|
1,3610
| 4,5
1,5041
| |
| x
f(x)
| 4,5
1,5041
| 4,9
1.5892
| 5,5
1,7047
| 6,0
1.7916
| |
| x
f(x)
| 3,5
1,2528
| 3,8
1,3350
| 4,5
1,5041
| 5,1
1.6292
| |
| x
f(x)
| 2,6
1,0296
| 3,3
1.1939
| 3,9
1,3610
| 4,6
1,5261
| |
| x
f(x)
| 4,1
1,4110
| 4,6
1,5261
| 5,2
1,6487
| 6,0
1,7918
| | | | | | | | | |
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
Основные структурные физиотерапевтические подразделения Физиотерапевтическое подразделение является одним из структурных подразделений лечебно-профилактического учреждения, которое предназначено для оказания физиотерапевтической помощи...
Почему важны муниципальные выборы? Туристическая фирма оставляет за собой право, в случае причин непреодолимого характера, вносить некоторые изменения в программу тура без уменьшения общего объема и качества услуг, в том числе предоставлять замену отеля на равнозначный...
Тема 2: Анатомо-топографическое строение полостей зубов верхней и нижней челюстей. Полость зуба — это сложная система разветвлений, имеющая разнообразную конфигурацию...
|
Принципы резекции желудка по типу Бильрот 1, Бильрот 2; операция Гофмейстера-Финстерера. Гастрэктомия Резекция желудка – удаление части желудка:
а) дистальная – удаляют 2/3 желудка б) проксимальная – удаляют 95% желудка. Показания...
Ваготомия. Дренирующие операции Ваготомия – денервация зон желудка, секретирующих соляную кислоту, путем пересечения блуждающих нервов или их ветвей...
Билиодигестивные анастомозы Показания для наложения билиодигестивных анастомозов:
1. нарушения проходимости терминального отдела холедоха при доброкачественной патологии (стенозы и стриктуры холедоха)
2. опухоли большого дуоденального сосочка...
|
|
