Пример вычислений в пакете MATHCAD.
Подпрограмма преобразования матрицы А к треугольному виду (предполагается, что все «ведущие» элементы не равны нулю):

В результате вызова функции, например, можно получить
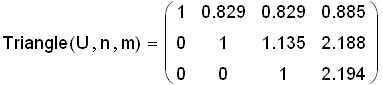
Программная реализация метода Гаусса для решения СЛАУ в пакете MATLAB.
function res = GaussSystem(A,b)
% вычисление корней системы уравнений
% матрица коэффициентов должна быть квадратной
% если матрица вырождена - решения нет
if (det(A)==0)
error('Определитель не может быть равен 0. Система не имеет решений');
end;
% определение размерности
n = size(A);
n = n(1);
% составление расширенной системы коэффициентов
B = [A b];
%=========Прямой ход================
for i=1:n
B(i,1:n+1) = B(i,1:n+1)./B(i,i);
for j=i+1:n
B(j,1:n+1) = B(j,1:n+1) - B(i,1:n+1).*B(j,i);
end;
end;
%========Обратный ход===============
x = zeros(n,1);
for k=n:-1:1
S=0;
for i=k+1:n
S=S+x(i,1)*B(k,i);
end;
x(k,1)= B(k,n+1)-S;
end;
res = x;
return
Вызов подпрограммы
>> A= [1.1 3.8 -0.93; 4.2 2.03 -1.21; 4.75 -1.28 4.26] – задание матрицы коэффициентов
>> b=[-5.06; 2.93; -4.85] – задание столбца свободных членов
>> GaussSystem(A,b)
ans =
0.9804
-2.3331
-2.9327
Варианты лабораторных работ
| Ва-ри-ант
| a11
| a12
| a13
| a14
| a21
| a22
| a23
| a24
| a31
| a32
| a33
| a34
|
|
| 1.21
| 4.05
| 2.11
| 4.25
| 0.75
| 1.21
| 3.21
| 7.42
| 2.27
| 5.66
| 3.06
| 10.5
|
|
| 5.96
| 1.40
| 5.03
| 7.41
| 2.99
| 1.25
| 0.38
| 4.48
| 1.05
| 3.57
| 1.92
| 15.1
|
|
| 2.87
| 2.67
| 2.85
| 2.14
| 3.55
| 0.71
| 1.25
| 0.95
| 1.13
| 4.81
| 2.14
| 1.32
|
|
| 6.62
| 2.65
| 2.45
| 2.57
| 5.21
| 0.21
| 2.13
| 2.17
| 1.15
| 4.21
| 1.75
| -1.90
|
|
| 2.00
| 2.60
| 1.93
| 2.15
| 3.45
| 0.58
| 1.21
| 1.55
| 1.25
| 4.21
| 1.95
| 2.10
|
|
| 1.25
| 2.25
| 3.75
| 2.00
| 1.75
| 3.25
| 2.05
| 1.80
| 2.35
| 1.25
| 1.85
| 6.70
|
|
| 0.75
| 1.23
| 3.19
| 1.79
| 3.48
| 1.61
| 1.95
| 4.95
| 0.46
| 5.26
| 5.32
| 14.7
|
|
| 3.58
| 2.77
| 2.34
| 1.91
| 5.21
| 2.13
| 0.49
| 3.42
| 1.17
| 3.90
| 2.14
| 15.4
|
|
| 2.70
| 2.61
| 3.24
| 3.05
| 2.48
| 0.18
| 1.71
| 2.55
| 1.20
| 3.48
| 0.97
| 1.35
|
|
| 7.44
| 2.46
| 2.74
| 3.05
| 5.41
| 1.25
| 2.01
| 2.57
| 1.15
| 3.81
| 0.92
| -1.15
|
|
| 1.26
| 4.20
| 1.97
| 4.21
| 0.71
| 1.91
| 3.88
| 2.00
| 2.20
| 4.79
| 3.16
| -5.01
|
|
| 1.11
| 4.83
| 2.15
| 5.01
| 1.75
| 2.16
| 5.01
| 2.25
| 2.43
| 5.52
| 3.39
| 5.21
|
|
| 3.40
| 2.82
| 2.82
| 3.01
| 4.18
| 1.25
| 0.95
| 1.15
| 1.71
| 3.95
| 0.25
| 0.57
|
|
| 1.08
| 3.50
| 1.90
| 4.15
| 3.01
| 0.15
| 5.41
| 1.27
| 0.06
| 1.70
| 5.79
| 13.1
|
|
| 1.17
| 1.19
| 1.77
| 4.25
| 1.39
| 1.45
| 4.60
| 1.55
| 4.06
| 5.42
| 3.88
| -6.01
|
|
| 1.21
| 3.59
| 0.99
| 3.75
| 1.50
| 0.87
| 4.21
| 1.05
| 1.28
| 3.66
| 2.68
| -3.91
|
|
| 1.10
| 3.80
| 0.93
| 4.20
| 2.03
| 1.21
| 4.75
| 1.28
| 4.26
| 5.06
| 2.93
| -4.85
|
|
| 1.13
| 6.92
| 2.17
| 14.2
| 2.41
| 1.13
| 4.48
| 10.5
| 4.04
| 6.03
| 2.63
| 13.0
|
|
| 1.70
| 3.94
| 0.26
| 1.85
| 0.78
| 1.57
| 3.77
| 0.95
| 5.89
| 2.70
| 0.71
| 5.32
|
|
| 2.51
| 0.20
| 1.75
| 2.15
| 1.52
| 0.90
| 4.23
| 4.35
| 2.72
| 2.61
| 3.24
| 3.58
|
|
| 2.40
| 1.15
| 4.50
| 0.09
| 6.38
| 1.77
| 1.65
| 13.8
| 5.25
| 2.15
| 0.50
| 11.4
|
|
| 1.42
| 1.45
| 4.61
| 1.58
| 2.56
| 2.77
| 6.33
| 2.85
| 5.18
| 1.25
| 2.16
| 6.21
|
|
| 1.72
| 2.10
| 4.95
| 2.01
| 3.51
| 0.75
| 1.28
| 3.61
| 4.67
| 4.10
| 0.89
| 4.55
|
|
| 5.39
| 1.24
| 2.03
| 4.98
| 2.03
| 1.24
| 4.72
| 2.42
| 3.18
| 2.60
| 5.67
| 3.52
|
|
| 3.44
| 0.60
| 1.19
| 3.50
| 0.74
| 1.90
| 3.90
| 0.85
| 5.45
| 1.72
| 3.14
| 6.05
|
|
| 0.80
| 1.61
| 3.76
| 1.75
| 2.19
| 1.26
| 0.94
| 1.29
| 0.93
| 2.38
| 4.02
| -2.50
|
|
| 2.42
| 3.17
| 8.45
| 3.07
| 1.18
| 2.14
| 4.11
| 1.38
| 4.46
| 6.45
| 8.17
| 3.95
|
|
| 1.24
| 2.37
| 3.48
| 3.17
| 0.76
| 4.21
| 2.25
| 2.44
| 8.84
| 0.96
| 5.27
| 3.06
|
|
| 6.21
| 4.52
| 5.16
| 5.24
| 7.49
| 5.34
| 4.16
| 5.86
| 4.15
| 9.48
| 9.20
| 1.71
|
|
| 4.42
| 12.6
| 5.77
| 1.56
| 0.16
| 3.82
| 6.41
| 4.42
| 7.14
| 4.98
| 8.73
| -2.67
|
Лабораторная работа № 5
ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ)
Цель работы:изучить итерационные методы решения СЛАУ,решить заданную систему линейных алгебраических уравнений методом простой итерации (метод Якоби) и методом Зейделя с точностью до  .
.


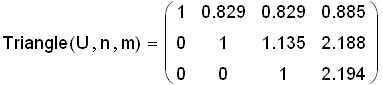
 .
.


