Пакет MATHCAD. Для поиска корней обычного многочлена p(x) степени n MATHCAD имеет очень удобную функцию: polyroot(V)

Для поиска корней обычного многочлена p(x) степени n MATHCAD имеет очень удобную функцию: polyroot(V). Она возвращает вектор корней многочлена степени n, коэффициенты которого находятся в векторе v, имеющем длину, равную n+1.

Заметим, что корни многочлена могут быть как вещественными, так и комплексными числами. Не рекомендуется пользоваться этой функцией, если степень полинома выше пятой-шестой, так как тогда трудно получить малую погрешность вычисления корней.

Для решения уравнений с одним неизвестным MATHCAD имеет встроенную функцию root,которая, в зависимости от типа задачи, может содержать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному: root(f(х), х); root(f(х), х,а,b),

где f(х) – скалярная функция, определяющая уравнение, х – скалярная переменная, относительно которой решается уравнение; а,b – границы интервала, внутри которого происходит поиск корня.

Первый тип функции root требует дополнительного задания начального значения (guess value) переменной х. Для этого нужно просто предварительно присвоить х некоторое число. Поиск корня будет производиться вблизи этого числа. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня.

Если правильное завершение работы функции root отсутствует, то это значит, что:

– нет корней;

– задание начальных условий некорректно (начальное условие слишком далеко от корней, несоответствие типов);

– на пути к корню встретился локальный экстремум;

– встретилась точка разрыва функции.

Для задания начальных условий удобнее всего построить график функции. Если в окрестности корня функция имеет малую кривизну, то экстремум рекомендуется искать в виде

.

Для нахождения второго корня необходимо либо задать другое начальное приближение, либо использовать вызов

,

где а – уже вычисленный корень.

Примеры использования функции root:

1) x:=nu root (F(x),x)=...;

2) если далее корень понадобится в выражениях, то, например, xv:=root (F(x),x).

Если точность мала, то изменением значения TOL -погрешности вычислений следует задать требуемую точность, например, TOL:=0,0001.

С помощью символьных преобразований также можно решать уравнения, неравенства.

Пример1. Найти корни уравнения .

Решение.

1. Ввести заданное уравнение. В качестве знака равенства следует использовать оператор отношения = с панели инструментов Boolean.

2. На панели инструментов Symbolic выбрать оператор
Solve ■ →.. В качестве требуемой переменной ввести x.

3. Щелкнуть левой кнопкой мыши за пределами введенной формулы. Справа от оператора →; появится результирующее значение:

.

Заметим, что данная последовательность действий остается верной и при наличии в уравнении параметра, например

.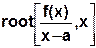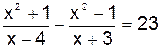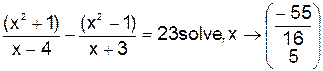