Пусть дано уравнение
 , (3.1)
, (3.1)
где  – непрерывная функция. Требуется вычислить действительный корень уравнения, находящийся на отрезке
– непрерывная функция. Требуется вычислить действительный корень уравнения, находящийся на отрезке  . Приводим заданное уравнение
. Приводим заданное уравнение  к эквивалентному виду
к эквивалентному виду
 , (3.2)
, (3.2)
где  – некоторая непрерывная на отрезке
– некоторая непрерывная на отрезке  функция.
функция.
Выбираем произвольное  и подставляем его в правую часть равенства (3.2):
и подставляем его в правую часть равенства (3.2):
 .
.
Аналогично получаем итерационную последовательность:
 ;
;
 ;
;
…………..
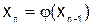 .
.
Доказано, что если итерационная последовательность  ,
,  ,
,  ,…,
,…,  ,… сходится, то её пределом является корень уравнения (3.2), а значит, и корень уравнения (3.1), так как уравнения (3.1) и (3.2) равносильны.
,… сходится, то её пределом является корень уравнения (3.2), а значит, и корень уравнения (3.1), так как уравнения (3.1) и (3.2) равносильны.
Для сходимости итерационного процесса достаточно исходное уравнение  привести к виду
привести к виду  так, чтобы выполнялось условие
так, чтобы выполнялось условие
 , (3.3)
, (3.3)
где  . При этом итерационная последовательность сходится независимо от выбора
. При этом итерационная последовательность сходится независимо от выбора  .
.
Итерации имеют геометрическую интерпретацию. Решение уравнения (3.2) является абсциссой точки пересечения прямой y = x и кривой y = φ(x). Геометрически видно, что если в окрестности решения выполняются неравенства 0 < φ’(x) ≤ М < 1, то последовательность {xK} монотонно сходится к  , причем с той стороны, с которой расположено начальное приближение (рис. 3.1).
, причем с той стороны, с которой расположено начальное приближение (рис. 3.1).
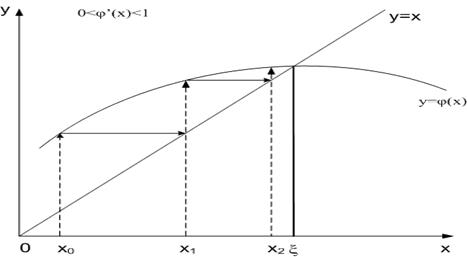
Рис. 3.1. Приближение к корню с одной стороны
В случае −1 < −M ≤ φ’(x) < 0 последовательные приближения расположены поочередно с разных сторон от решения  (рис. 3.2).
(рис. 3.2).

Рис. 3.2. Приближение к корню с разных сторон
Уравнение  можно преобразовать к виду
можно преобразовать к виду  разными способами, лишь бы функция
разными способами, лишь бы функция  удовлетворяла условию (3.3). Например, уравнение
удовлетворяла условию (3.3). Например, уравнение  заменяем равносильным
заменяем равносильным  . В этом случае
. В этом случае  . Параметр
. Параметр  выбираем так, чтобы
выбираем так, чтобы  ½ при
½ при  .
.
Пример 1. Привести уравнение  к виду, пригодному для применения метода итераций. Единственный действительный корень заданного уравнения находится на отрезке
к виду, пригодному для применения метода итераций. Единственный действительный корень заданного уравнения находится на отрезке  , так как
, так как  ,
,  .
.
Приводим исходное уравнение к виду  .В этом случае
.В этом случае  . Тогда
. Тогда  ,
,  при
при  .
.
Таким образом, достаточное условие сходимости итерационного процесса выполняется. Метод итераций применим для решения полученного уравнения. Выбираем произвольное 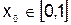 , например,
, например, 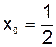 , и начинаем процесс метода итераций.
, и начинаем процесс метода итераций.
Пример 2. Привести уравнение  к виду, пригодному для применения метода итераций.
к виду, пригодному для применения метода итераций.
Единственный корень заданного уравнения находится на отрезке  . Рассмотренный в примере 1 способ в данном случае неприменим, так как при этом не удовлетворяется достаточное условие сходимости итерационного процесса. Заменяем исходное уравнение равносильным:
. Рассмотренный в примере 1 способ в данном случае неприменим, так как при этом не удовлетворяется достаточное условие сходимости итерационного процесса. Заменяем исходное уравнение равносильным:
 .
.
В этом случае
 ,
,  .
.
Параметр  находим из условия
находим из условия  ê при
ê при 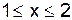 , т.е.
, т.е.  или
или  при
при 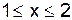 . Отсюда
. Отсюда  . Полагаем, например,
. Полагаем, например,  . Исходное уравнение преобразуем к виду
. Исходное уравнение преобразуем к виду
 ,
,
причем  при
при  .
.
Выбираем произвольное  . Пусть
. Пусть  , вычисляем
, вычисляем  . Подставляя
. Подставляя  в правую часть равенства, получаем
в правую часть равенства, получаем  и т.д. Вычисления производим до тех пор, пока выполнится неравенство
и т.д. Вычисления производим до тех пор, пока выполнится неравенство  .
.
Скорость сходимости итерационного процесса определяется неравенством
 ,
,
где  – точное решение уравнения.
– точное решение уравнения.
Оценка погрешности метода простой итерации записывается в виде
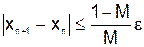 ,
,
где  – заданная точность решения. В частности, при
– заданная точность решения. В частности, при  и
и  величина
величина  будет приближенным значением корня
будет приближенным значением корня  с точностью до
с точностью до  , т.е.
, т.е.  .
.

 , (3.1)
, (3.1) – непрерывная функция. Требуется вычислить действительный корень уравнения, находящийся на отрезке
– непрерывная функция. Требуется вычислить действительный корень уравнения, находящийся на отрезке  . Приводим заданное уравнение
. Приводим заданное уравнение  , (3.2)
, (3.2) – некоторая непрерывная на отрезке
– некоторая непрерывная на отрезке  и подставляем его в правую часть равенства (3.2):
и подставляем его в правую часть равенства (3.2): .
. ;
; ;
;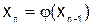 .
. ,
,  ,
,  ,…,
,…,  ,… сходится, то её пределом является корень уравнения (3.2), а значит, и корень уравнения (3.1), так как уравнения (3.1) и (3.2) равносильны.
,… сходится, то её пределом является корень уравнения (3.2), а значит, и корень уравнения (3.1), так как уравнения (3.1) и (3.2) равносильны. , (3.3)
, (3.3) . При этом итерационная последовательность сходится независимо от выбора
. При этом итерационная последовательность сходится независимо от выбора  , причем с той стороны, с которой расположено начальное приближение (рис. 3.1).
, причем с той стороны, с которой расположено начальное приближение (рис. 3.1).

 . В этом случае
. В этом случае  . Параметр
. Параметр  выбираем так, чтобы
выбираем так, чтобы  ½ при
½ при  к виду, пригодному для применения метода итераций. Единственный действительный корень заданного уравнения находится на отрезке
к виду, пригодному для применения метода итераций. Единственный действительный корень заданного уравнения находится на отрезке  , так как
, так как  ,
,  .
. .В этом случае
.В этом случае  . Тогда
. Тогда  ,
,  при
при  .
.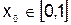 , например,
, например, 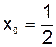 , и начинаем процесс метода итераций.
, и начинаем процесс метода итераций. к виду, пригодному для применения метода итераций.
к виду, пригодному для применения метода итераций. . Рассмотренный в примере 1 способ в данном случае неприменим, так как при этом не удовлетворяется достаточное условие сходимости итерационного процесса. Заменяем исходное уравнение равносильным:
. Рассмотренный в примере 1 способ в данном случае неприменим, так как при этом не удовлетворяется достаточное условие сходимости итерационного процесса. Заменяем исходное уравнение равносильным: .
. ,
,  .
. находим из условия
находим из условия 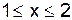 , т.е.
, т.е.  или
или  при
при  . Полагаем, например,
. Полагаем, например,  . Исходное уравнение преобразуем к виду
. Исходное уравнение преобразуем к виду ,
, при
при  .
. . Пусть
. Пусть  , вычисляем
, вычисляем  . Подставляя
. Подставляя  .
. ,
,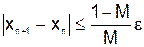 ,
, – заданная точность решения. В частности, при
– заданная точность решения. В частности, при  и
и  величина
величина  будет приближенным значением корня
будет приближенным значением корня  .
.


