Теоретические сведения. 1. Метод линейной интерполяции (метод хорд).Пусть дано уравнение , где функция непрерывна на [a;b] и f(a)f(b)<0
1. Метод линейной интерполяции (метод хорд ). Пусть дано уравнение
Далее, применив этот прием к тому из отрезков ([a;x1] или [x1;b]), на концах которого функция f(x)имеет противоположные знаки, получим второе приближение корня x2и т.д. Геометрически способ пропорциональных частей эквивалентен замене кривой y = f(x) хордой, проходящей через точки A(a;f(a)) и B(b;f(b)) (рис. 2.1).
Рис. 2.1. Геометрическая интерпретация метода хорд
В самом деле, уравнение хорды AB есть Отсюда, полагая x=x1 и y=0, получаем Для сходимости метода хорд необходимо, чтобы выполнялись следующие условия: а) неподвижен тот конец хорды, для которого знак функции f(x) совпадает со знаком ее второй производной f”(x); б) последовательные приближения xn лежат по ту сторону корня ξ, где функция f(x) имеет знак, противоположный знаку ее второй производной f”(x). Расчетная формула метода в случае неподвижной точки a:
Если отрезок [a;b] достаточно мал, то погрешность метода определяется так:
Таким образом, в этом случае, как только будет выполняться условие 2. Метод Ньютона (метод касательных). Пусть Положим 0 = Следовательно,
Внеся эту поправку в формулу уточнения корня, можно найти следующее (по порядку) приближение корня:
Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой y = f(x) касательной, проведённой в некоторой точке кривой (рис. 2.2).
Рис. 2.2. Геометрическая интерпретация метода Ньютона
Теорема. Если
единственный корень Применяя метод Ньютона, следует руководствоваться следующим правилом: в качестве исходной точки Условием завершения итерационного процесса является выполнение неравенства 3. Модифицированный метод Ньютона. Если производная f’(x) мало изменяется на отрезке [a, b], то в расчетной формуле метода касательных можно положить Отсюда для корня
Геометрически этот способ означает, что заменяются касательные в точках Bn[xn, f(xn)] прямыми, параллельными касательной к кривой y = f(x), в её фиксированной точке B0[x0, f(x0)] (рис. 2.3). Эта формула весьма полезна, если
Рис. 2.3. Геометрическая интерпретация модифицированного метода Ньютона
4. Метод секущих. В алгоритме Ньютона требуется вычислить две функции для каждой итерации – В методе секущих используется такая же формула, как и в методе хорд, но существуют различные логические решения относительно способа поиска каждого последующего члена. Необходимо около точки
Рис. 2.4. Геометрическая интерпретация метода секущих Уравнение, связывающее
Значения m в формуле равны тангенсу угла наклона секущей, которая проходит через два первых приближения к тангенсу угла наклона прямой, проходящей через точки Общий член, определенный согласно двухточечной итерационной формуле:
Условие завершения процесса приближений такое же, как и в методе Ньютона. 5. Комбинированный метод. Метод, используемый для вычисления значения корня с заданной точностью, заключается в поочередном применении метода хорд и метода касательных. Концы отрезка, содержащего корень уравнения, обозначим
Рис. 2.5. Геометрическая интепретация комбинированного метода Расчётные формулы комбинированного метода для случая, приведенного на рис. 2.5, имеют следующий вид:
где Если корень уравнения требуется вычислить с точностью до Погрешность численного решения уравнения. Для оценки точности приближения можно воспользоваться формулой
Приведем еще формулу, позволяющую оценивать абсолютную погрешность приближенного значения
Примем для определенности, что последовательные приближения
где конец
Применив теорему Лагранжа о конечном приращении функции, получим
где
Поскольку Из выражения (2.1) выводим формулу
где за Таким образом, в этом случае, как только будет выполняться условие
где
|

 , где функция
, где функция  непрерывна на [a;b] и f(a)f(b)<0. Для определенности положим f(a)>0 и f(b)<0. Тогда, вместо того чтобы делить отрезок [a;b] пополам (как это делается в методе половинного деления), более естественно поделить его в отношении f(a)/f(b). Это дает приближенное значение корня x1=b+h1, где
непрерывна на [a;b] и f(a)f(b)<0. Для определенности положим f(a)>0 и f(b)<0. Тогда, вместо того чтобы делить отрезок [a;b] пополам (как это делается в методе половинного деления), более естественно поделить его в отношении f(a)/f(b). Это дает приближенное значение корня x1=b+h1, где

 .
. .
.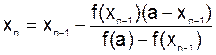 .
.
 .
.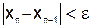 , где ε – заданная предельная абсолютная погрешность, гарантировано, что
, где ε – заданная предельная абсолютная погрешность, гарантировано, что  .
. – корень уравнения
– корень уравнения 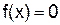 – отделен на отрезке [a, b], причем
– отделен на отрезке [a, b], причем  и
и  непрерывны и сохраняют определенные знаки при
непрерывны и сохраняют определенные знаки при  .
. , где
, где  считаем малой величиной. Отсюда, применив формулу Тейлора, получим
считаем малой величиной. Отсюда, применив формулу Тейлора, получим .
.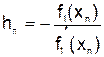 .
. (n = 0, 1, 2,...).
(n = 0, 1, 2,...).
 , причем
, причем  и
и  , то, исходя из начального приближения
, то, исходя из начального приближения  , удовлетворяющего неравенству
, удовлетворяющего неравенству  , можно вычислить методом Ньютона
, можно вычислить методом Ньютона
 уравнения
уравнения  с любой степенью точности.
с любой степенью точности. выбирается тот конец интервала
выбирается тот конец интервала  , которому отвечает ордината того же знака, что и знак
, которому отвечает ордината того же знака, что и знак  , где ε – заданная предельная абсолютная погрешность.
, где ε – заданная предельная абсолютная погрешность. ≈
≈  .
. (n = 0, 1, 2,...).
(n = 0, 1, 2,...).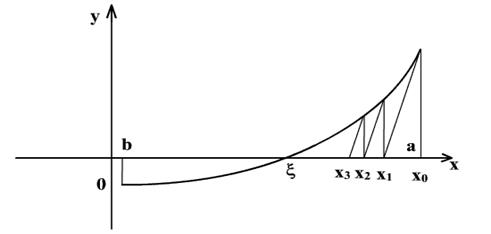
 и
и  . Метод секущих требует только одного вычисления функции
. Метод секущих требует только одного вычисления функции  при одной итерации, и простой корень имеет порядок сходимости R
при одной итерации, и простой корень имеет порядок сходимости R  1,618033989. Этот метод почти так же быстр, как и метод Ньютона, который имеет порядок сходимости R=2.
1,618033989. Этот метод почти так же быстр, как и метод Ньютона, который имеет порядок сходимости R=2. иметь две начальные точки
иметь две начальные точки  и
и  , как показано на рис. 2.4. Определим
, как показано на рис. 2.4. Определим  как абсциссу точки пересечения линии, проходящей через эти две точки, и оси 0X. Тогда на рис. 2.4 видно, что
как абсциссу точки пересечения линии, проходящей через эти две точки, и оси 0X. Тогда на рис. 2.4 видно, что  или
или  .
.
 и
и  и
и 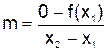 .
. .
.
 и
и  . Условимся обозначать через
. Условимся обозначать через 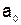 тот конец отрезка, на котором знаки функции
тот конец отрезка, на котором знаки функции  совпадают. Через точки
совпадают. Через точки  ,
,  проведём хорду. Точку пересечения хорды с осью
проведём хорду. Точку пересечения хорды с осью  обозначим через
обозначим через  . В точке
. В точке  . Точку пересечения касательной с осью
. Точку пересечения касательной с осью  . Итак, получен новый отрезок с концами
. Итак, получен новый отрезок с концами  ,
,  и т.д.
и т.д.
 ,
, 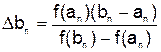 ;
; ,
, 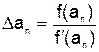 ,
, .
. , то процесс вычисления корня можно прекращать в тот момент, когда
, то процесс вычисления корня можно прекращать в тот момент, когда  . В качестве ответа взять среднее арифметическое последних полученных значений
. В качестве ответа взять среднее арифметическое последних полученных значений  и
и  , т.е.
, т.е.  .
. ,
, 

 , если известны два последовательных приближения
, если известны два последовательных приближения  и
и  непрерывна на отрезке
непрерывна на отрезке  , содержащем все приближения, и сохраняет постоянный знак, причем
, содержащем все приближения, и сохраняет постоянный знак, причем .
.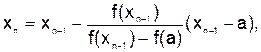 (n = 1,2,…),
(n = 1,2,…), является неподвижным. Отсюда будем иметь
является неподвижным. Отсюда будем иметь .
. ,
, и
и  . Следовательно
. Следовательно (2.1)
(2.1) и
и  , то, очевидно, имеем
, то, очевидно, имеем 
 , (2.2)
, (2.2) могут быть взяты соответственно наименьшее и наибольшее значения модуля производной
могут быть взяты соответственно наименьшее и наибольшее значения модуля производной  то из формулы (2.2) получаем
то из формулы (2.2) получаем  .
. ,
, .
.


