Формирование базы правил систем нечеткого вывода
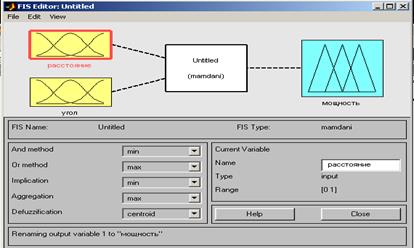
Следующим этапом построения модели является построение базы правил. С этой целью преобразуем рассмотренные выше 5 эвристических правил в 6 правил нечетких продукций: 2 5.1 систем ется закрепления навыков разработки и исследования нечетких моделей управления ПРАВИЛО-1: ЕСЛИ "расстояние далекое" И "угол равен нулю" ТО "мощность положительная средняя"; ПРАВИЛО-2: ЕСЛИ "расстояние далекое" И "угол отрицательный малый" ТО "мощность положительная большая"; ПРАВИЛО-3: ЕСЛИ "расстояние далекое" И "угол отрицательный большой" ТО"мощность положительная средняя"; ПРАВИЛО-4: ЕСЛИ "расстояние среднее" И "угол отрицательный малый" ТО "мощность отрицательная средняя"; ПРАВИЛО-5: ЕСЛИ "расстояние близкое" И "угол положительный малый" ТО "мощность положительная средняя"; ПРАВИЛО_6: ЕСЛИ "расстояние ноль" И "угол равен нулю" ТО "мощность равна нулю". Для решения этой задачи была построена база правил соответствующей системы нечеткого вывода, которая содержит 6 правил нечетких продукций следующего вида: ПРАВИЛО-1: ЕСЛИ "β1 есть РВ" И "β2 есть Z", ТО "βз есть РМ"; ПРАВИЛО-2: ЕСЛИ "β1 есть РВ" И "β2 есть NS ", ТО "βз есть PB "; ПРАВИЛО-3: ЕСЛИ "β1 есть P В" И "β2 есть NB ", ТО "βз есть РМ"; ПРАВИЛО-4: ЕСЛИ "β1 есть РM" И "β2 есть NS ", ТО "βз есть N М"; ПРАВИЛО-5: ЕСЛИ "β1 есть РS" И "β2 есть PS ", ТО "βз есть РМ"; ПРАВИЛО-6: ЕСЛИ "β1 есть Z " И "β2 есть Z", ТО "βз есть Z ". Для сокращенной записи правил используются следующие обозначения: β1 — первая входная лингвистическая переменная с именем "расстояние", β;2— вторая входная лингвистическая переменная с именем "угол", β3 — выходная лингвистическая переменная с именем "мощность". В качестве терм-множества первой лингвистической переменной используется множество T1= {"нуль", "близкое", "среднее", "далекое"}, которое записывается в символическом виде: T1 = {Z, PS, РМ, РВ}. В качестве терм-множества второй лингвистической переменной используется множество Т2= {"отрицательный большой", "отрицательный малый", "нуль", "положительный малый"}, которое записывается в символическом виде: T2={NB. NS, Z, PS}. В качестве терм-множества выходной лингвистической переменной используется множество Tз= {"отрицательная средняя", "нуль", "положительная средняя", "положительная большая"}, которое записывается в символическом виде: T3={NM, Z, РМ, РВ}. Разработку нечеткой модели (назовем ее crane) также будем выполнять с использованием графических средств системы MATLAB. С этой целью откроем редактор FIS и определим 2 входные переменные с именами "расстояние" (β1) и "угол" (β2) и одну выходную переменную с именем "мощность" (βз). Вид графического интерфейса редактора FIS для этих переменных изображен на рисунке 6.2.
Рисунок 6.2. Графический интерфейс редактора FIS после определения входных и выходных переменных для системы нечеткого вывода crane
Оставим без изменения тип системы нечеткого вывода, предложенный системой MATLAB по умолчанию, поскольку будем использовать систему нечеткого вывода типа Мамдани. Нет необходимости изменять и другие параметры разрабатываемой нечеткой модели, предложенные системой MATLAB по умолчанию, такие как логические операции (min — для нечеткого логического И, max — для нечеткого логического ИЛИ), методы импликации (min). агрегирования (max) и метода дефаззификации (centroid).
-10 -5 0 5 10 15 20 25 30 Рисунок 6.3. Функции принадлежности для переменной «Расстояние»
Далее следует определить функции принадлежности термов для каждой из переменных системы нечеткого вывода. Для этой цели воспользуемся редактором функций принадлежности системы MATLAB. Для первой входной переменной следует добавить один дополнительный терм к трем, заданным по умолчанию, и определить параметры соответствующих функций принадлежности. Численные значения этих параметров можно взять из рисунка 6.3. Вид графического интерфейса редактора функций принадлежности после задания первой входной переменной изображен на рисунке 6.4.
Рисунок 6.4. Графический интерфейс редактора функций принадлежности
Для второй входной переменной "угол" также следует определить 4 терма, изменив диапазон значений переменной и параметры треугольных функций принадлежности термов (см. Рис. 6.5).
-900 -67,50 -450 -22,50 00 22,50 450 67,50 900 Рисунок 6.5. Функции принадлежности для переменной «Угол»
Для выходной переменной "мощность" следует определить 4 терма, изменить диапазон значений переменной и определить соответствующие функции принадлежности термов. Поскольку функции принадлежности термов выходной переменной равны постоянным значениям (см. Рис. 5.6), а среди встроенных функций принадлежности системы MATLAB отсутствуют одноточечные функции принадлежности, то в качестве функций принадлежности термов возьмем треугольные функции принадлежности с подходящими значениями параметров.
-30 -22,5 -15 -7,5 0 7,5 15 22,5 30 Рисунок 6.6. Функции принадлежности для переменной «Мощность» Вид графического интерфейса редактора функций принадлежности после задания выходной переменной изображен на рисунке 6.7.
Рисунок 6.7. Графический интерфейс редактора функций принадлежности "мощность" для системы нечеткого вывода crane
Теперь зададим 6 правил для разрабатываемой системы нечеткого вывода. Для этой цели воспользуемся редактором правил системы MATLAB. Вид графического интерфейса редактора правил после задания всех 6 правил нечеткого вывода изображен на рисунке 6.8.
Рисунок 6.8. Графический интерфейс редактора правил после задания базы правил для системы нечеткого вывода crane Теперь можно выполнить оценку построенной системы нечеткого вывода для задачи автоматического управления портовым краном. С этой целью откроем программу просмотра правил системы MATLAB и введем значения входных переменных для частного случая, когда текущее расстояние до цели равно 7.5 м, а угол между контейнером и кабиной крана равен 10°. Процедура нечеткого вывода, выполненная системой MATLAB для разработанной нечеткой модели, выдает в результате значение выходной переменной "мощность", равное 12 киловатт (Рис. 6.9).
Рисунок 6.9. Графический интерфейс программы просмотра правил после выполнения процедуры нечеткого вывода для значений входных переменных [7,5 10]
Данное значение соответствует включению двигателя крана для движения вправо (в положительном направлении), при этом сама мощность равна 12 киловатт. В данном случае сравнение результатов нечеткого вывода для этих значений входных переменных, полученных на основе численных расчетов и с помощью разработанной нечеткой модели MATLAB, также показывает согласованность модели и подтверждает ее адекватность (при проверке в «ручном» режиме). Для общего анализа разработанной нечеткой модели также может оказаться полезной визуализация соответствующей поверхности нечеткого вывода (Рис. 6.10).
Рисунок 6.10. Визуализация поверхности нечеткого вывода для системы нечеткого вывода crane Данная поверхность нечеткого вывода позволяет установить зависимость значений выходной переменной от значений входных переменных нечеткой модели системы управления краном. Эта зависимость может послужить основой для программирования контроллера или аппаратной реализации соответствующего нечеткого алгоритма управления в форме соответствующей таблицы решений. Рассмотренные примеры иллюстрируют все практические действия, которые необходимо выполнить для разработки и использования нечетких моделей в форме систем нечеткого вывода. При этом соответствующие графические средства системы MATLAB позволяют реализовать все этапы процесса нечеткого моделирования в удобной для пользователя форме.
|