В интерактивном режиме

Цель работы. Укрепить приобретенные в работе №2 навыки работы с инструментом Fuzzy Logic Toolbox на конкретном примере нечеткого моделирования. В качестве примера разработки системы нечеткого вывода в интерактивном режиме с помощью графических средств пакета Fuzzy Logic Toolbox рассмотрим следующую нечеткую модель, которая входит в число демонстрационных примеров системы MATLAB.

Пример "Чаевые в ресторане". Рассмотрим ситуацию в ресторане, при которой, согласно принятым в США традициям, после окончания обслуживания посетителя принято оставлять официанту чаевые. Основываясь на устоявшихся в этой стране обычаях и интуитивных представлениях посетителей ресторанов величина суммы чаевых не является постоянной и зависит, например, от качества обслуживания и качества приготовления заказанных блюд. Задача состоит в том, чтобы разработать некоторую экспертную систему, кото­рая была бы реализована в виде системы нечеткого вывода и позволяла бы определять величину чаевых на основе субъективных оценок посетителей качества обслуживания и качества приготовления заказанных блюд.

Эмпирические знания о рассматриваемой проблемной области могут быть представлены в форме следующих эвристических правил продукций:

1. Если обслуживание плохое или ужин подгоревший, то чаевые — малые.

2. Если обслуживание хорошее, то чаевые — средние.

3. Если обслуживание отличное или ужин превосходный, то чаевые – щедрые.

В качестве входных параметров системы нечеткого вывода будем рассматривать 2 нечеткие лингвистические переменные: "качество обслуживания" и "качество приготовления заказанных блюд" (или сокращенно — "качество ужина"), а в качестве выходных параметров — нечеткую лингвистическую переменную "величина чаевых";.В качестве терм-множества первой лингвистической переменной "качество обслуживания" будем использовать множество T1= { "плохое", "хорошее", "отличное"}, а в качестве терм-множества второй лингвистической переменной "качество ужина" будем использовать множество Т2={"подгоревший", "превосходный"}. В качестве терм-множества выходной лингвистической переменной "величина чаевых" будем использовать множество Т3= {"малые", "средние", "щедрые"}. При этом каждый из термов первой и второй входной переменной (качество обслуживания и приготовления заказанных блюд) будем оценивать по 10-балльной порядковой шкале, при которой цифре 0 соответствует наихудшая оценка, а цифре 10 — наилучшая оценка. Что касается термов выходной переменной, то будем предполагать, что малые чаевые составляют около 5% от стоимости заказанных блюд, средние чаевые — около 15%, а щедрые чаевые — около 25%.

С учетом сделанных уточнений, рассмотренная субъективная информация о величине чаевых может быть представлена в форме 3-х правил нечетких продукций следующего вида (система нечеткого вывода типа Мамдани):

ПРАВИЛО_1: ЕСЛИ "качество обслуживания плохое" ИЛИ "ужин подгоревший"; ТО "величина чаевых малая";

ПРАВИЛО_2: ЕСЛИ "качество обслуживания хорошее"; ТО "величина чаевых средняя";

ПРАВИЛО_3: ЕСЛИ "качество обслуживания отличное" ИЛИ "ужин превосходный" ТО "величина чаевых щедрая";.

Процесс разработки системы нечеткого вывода в интерактивном режиме для рассмотренного выше примера "Чаевые в ресторане" состоит в выполнении сле­дующей последовательности действий:

 

 

Рисунок 3.1. Вид редактора FIS после добавления второй входной переменной

 

1. Вызвать редактор систем нечеткого вывода FIS, для чего в окне команд набрать имя соответствующей функции fuzzy. После выполнения этой команды на экране появится графический интерфейс редактора FIS с именем системы нечеткого вывода Untitled и типом системы нечеткого вывода (Мамдани), предложенными по умолчанию (см. Рис. 3.1).

2. Поскольку в примере «Чаевые в ресторане» рассматривается система нечеткого вывода с двумя входами, необходимо добавить в разрабатываемую систему FIS еще одну входную переменную. Для этого следует выполнить команду меню Edit>Add Variable... >Input. В результате выполнения этой команды на диаграмме системы нечеткого вывода появится новый желтый прямоугольник с именем второй входной перемен: input2 (Рис. 3.1).

3. Изменим имена входных и выходных переменных, предложенных системой MATLAB по умолчанию. Для этого необходимо выделить прямоугольник с именем соответствующей переменной, выполнив щелчок на его изображении на диаграмме (стороны выделенного прямоугольника имеют красный цвет). После чего следует набрать новое имя переменной в поле ввода Name в пра­вой части редактора FIS. Результат изменения имен переменных системы не­четкого вывода изображен на рисунке 3.2.

 

 

Рисунок 3.2. Вид редактора FIS после изменения имен переменных, предложенных системой MATLAB по умолчанию

 

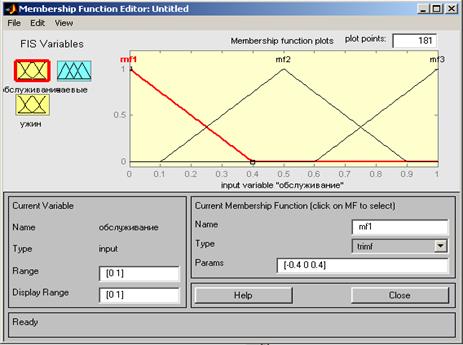
4. Изменим имя системы нечеткого вывода (Untitled), предложенное по умолча­нию. Для этого сохраним создаваемую структуру FIS во внешнем файле с именем, например - mytip. fis, выполнив команду меню File>Export>To Disk.... При этом будет вызвано стандартное диалоговое окно сохранения файла, в котором пользователю предлагается ввести имя соответствующего файла (расширение файла приписывается автоматически). Оставим без изменения предложенные системой MATLAB по умолчанию: метод нечеткого логического И (And method) — значение "min", метод нечеткого логического ИЛИ (Or method) — значение "max", метод импликации (Implication) — значение "min", метод аг­регирования (Aggregation) — значение "max" и метод дефаззификации (Defuzziflcation) — значение "centroid". Очевидно, эти значения могут быть изменены пользователем.

5. Теперь необходимо определить термы и их функции принадлежности для входных и выходных переменных нашей системы нечеткого вывода. Для этой цели следует воспользоваться редактором функций принадлежности, который может быть вызван одним из следующих способов:

• двойным щелчком на значке прямоугольника с именем соответствующей переменной;

• командой меню Edit>Membership Functions... (предварительно должен быть выделен

прямоугольник с именем соответствующей переменной);

• нажатием клавиш <Ctrl>+<2> (предварительно также должен быть выде­лен прямоугольник с именем соответствующей переменной).

После вызова редактора функций принадлежности каждой из переменных по умолчанию предлагается 3 терма с треугольными функции принадлеж­ности (Рис. 3.3).

Вначале изменим диапазон определения значений входных переменных, для чего в полях ввода Range и Display Range изменим верхнее значение с 1 на 10 (баллов). Аналогично выполняются изменения соответствующих диапазонов для выходной переменной "чаевые", при этом верхнее значе­ние 1 следует заменить на 30 (%). Изменения подтверждаются нажатием на клавишу <Enter> на клавиатуре.

 

 

Рисунок 3.3. Вид редактора функций принадлежности после его вызова

с функциями принадлежности для термов переменной "обслуживание";, предложенных системой MATLAB по умолчанию.

 

Далее изменим названия термов первой входной переменной "обслужи­вание", предложенные системой MATLAB по умолчанию (mfl, mf2, mf3) на "плохое", "хорошее", "отличное" соответственно. После чего изменим тип функций принадлежности первой переменной, предложенный по умолчанию, на функции типа Гаусса (gaussmf), выбрав соответствующий пункт в поле Туре. Параметры вновь заданных функций принадлежности оставим без изменения. Вид редактора функций принадлежности после внесенных изменений для первой из входных переменных изображен на рисунке 3.4.

 

 

Рисунок 3.4. Вид редактора функций принадлежности после изменения названия

термов и типа их функций принадлежности для первой входной

переменной "обслуживание";

 

Аналогичным образом изменим названия термов второй входной переменной "ужин" и удалим один из термов с соответствующей функцией принадлежно­сти. Для удаления терма следует выделить удаляемую функцию принадлежно­сти и нажать клавишу <Delete> на клавиатуре. Переход к редактированию переменной осуществляется щелчком на изображении прямоугольника с име­нем необходимой переменной.

Для переменной "ужин" изменим тип функций принадлежности ее термов на трапециевидные функции (trapmf) и их пара­метры следующим образом: для терма "подгоревший" зададим параметры [0 0 1 3], а для терма "превосходный" — [7 9 10 10].

Вид редактора функций принадлежности после внесенных изменений для второй входной переменной изображен на рисунке 3.5.

Наконец, изменим названия термов и параметры функций принадлежности для выходной переменной "чаевые", оставив без изменения треугольный тип функ­ций принадлежности, предложенный системой MATLAB. Для терма "малые" зададим параметры [0 5 10], а для терма "средние";— [10 15 20], для терма "щедрые" — [20 25 30]. Вид редактора функций принадлежности после сделан­ных изменений для выходной переменной "чаевые" изображен на рисунке 3.6.

6. Теперь настала очередь определить правила нечеткого вывода для разрабатываемой экспертной системы. Для этой цели следует воспользоваться редактором правил, который может быть вызван одним из следующих способов:

 

Рисунок 3.5. Вид редактора функций принадлежности после изменения названия термов и типа их функций принадлежности для второй входной переменной “ужин”

 

 

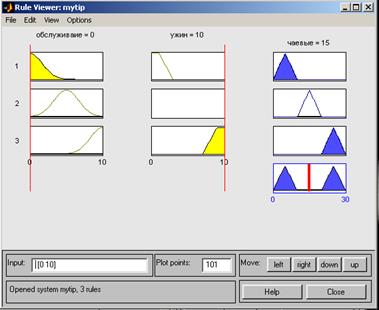
Рисунок 3.6. Редактор функций принадлежности после изменения названия термов и типа их функций принадлежности для входной переменной "обслуживание";

• двойным щелчком на значке квадрата в центре с именем создаваемой системы нечеткого вывода (myfis);

• командой меню Edit>Rules...;

• нажатием клавиш <Ctrl>+<3>.

Поскольку первоначально база правил нечеткого вывода пуста, то после вызова редактора правил центральное многострочное поле ввода не содержит никаких правил. Для их определения следует использовать поля меню и пере­ключатели в нижней части графического интерфейса редактора правил.

Для задания первого правила следует оставить выделенные по умолчанию поле с именем терма "плохое" для первой входной переменной, поле с именем терма "подгоревший" для второй входной переменной и поле с именем терма "малые" для выходной переменной.

Далее следует переключатель Connection поставить в положение or (логическое ИЛИ) и нажать на кнопку Add rule. После этого первое правило с символами кириллицы отобразится в верхнем окне.

Аналогичным образом задается второе правило, для которого следует выде­лить имена термов "хорошее", "попе" и "средние";, и третье правило с именами термов "античное", "превосходный" и "щедрые" для соответствующих перемен­ных. Вид редактора правил после их определения для разрабатываемой экспертной системы изображен на рисунке 3.7.

Заметим, что в поле ввода Weight отображается вес каждого правила, кото­рый можно изменять в пределах интервала [0, 1] (оставим без изменения его значение по умолчанию, равное 1 для всех правил). Этот же вес правил запи­сывается в круглых скобках в окне правил после каждого из правил нечеткого вывода.

7. После задания правил нечеткого вывода оказывается возможным получить результат нечеткого вывода (значение выходной переменной) для конкретных значений входных переменных. С этой целью необходимо открыть программу просмотра правил одним из следующих способов:

• командой меню View>Rules редактора FIS;

• командой меню View>Rules редактора функций принадлежности;

• командой меню View>RuIes редактора правил;

• нажатием клавиш <Ctrl>+<5>.

После вызова программы просмотра правил для нашей системы нечеткого вывода по умолчанию для входных переменных предложены средние значе­ния из интервала их допустимых значений (значения [5 5] в поле ввода Input). Это означает, что посетитель ресторана оценивает качество обслуживания в 5 баллов и качество ужина также в 5 баллов. Этим значениям входных пере­менных соответствует значение чаевых в 15%, которое отображается выше прямоугольников правил в правой части окна программы просмотра.

 

 

Рисунок 3.7.Вид редактора правил нечеткого вывода после их определения

Изменим значения входных переменных для другого случая, которому соответствует качество обслуживания в 0 баллов ("хуже некуда") и качество ужина в 10 баллов ("лучше не бывает"). Для этого курсор мыши переместим в поле ввода Input и введем соответствующие значения входных переменных: [0 10]. Система MATLAB оставит значение чаевых без изменения (15%), однако на диаграмме правил можно заметить результаты выполненных изменений (Рис. 3.8).

Поскольку процесс нечеткого моделирования предполагает анализ результа­тов нечеткого вывода при различных значениях входных переменных с целью установления адекватности разработанной нечеткой модели (в данном случае— экспертной системы), рассмотрим и другие случаи. Предположим, что качество обслуживания оценивается в 10 баллов ("лучше не бывает"), а качество ужина — в 2 балла ("бывает и хуже, но реже"). Введем соответствующие значения переменных аналогичным способом. В этом случае разработанная система нечеткого вывода рекомендует нам оставить чаевые в размере 16.4%.

 

 

Рисунок 3.8. Вид программы просмотра правил нечеткого вывода после изменения значений входных переменных на [0 10]

Если же предположить, что качество обслуживания по прежнему отличное (10 баллов), а качество ужина несколько улучшилось и оценивается в 3 балла, то величина чаевых существенно изменится и станет равной 24.7%. Более того, дальнейшее увеличение качества ужина не оказывает изменения величины чаевых. В частности, для значений входных переменных [10 10] величина чаевых составит по-прежнему 24.7%. Если некоторым из посетителей такая экспертная система покажется неадекватной (в частности, для случая значений входных переменных [10 10] можно бы оставить максимальные чаевые в 30%), то разработанная система нечеткого вывода потребует модификации. Данная модификация может потребовать изменения существующих правил или добавления новых, а также изменения параметров функции принадлежности входных и выходной переменных. Более тонкая настройка модели может быть связана с увеличением количества термов для каждой из входных и вы­ходных переменных, что, в свою очередь, приведет к увеличению количества правил в системе нечеткого вывода и общему усложнению модели. Все это предлагается выполнить читателям самостоятельно в качестве упражнения.

8.Для окончательного анализа разработанной нечеткой модели может оказаться полезной программа просмотра поверхности нечеткого вывода, которая может быть вызвана одним из следующих способов:

• командой меню View>Surface редактора FIS; • командой меню View>Surface редактора функций принадлежности;

• командой меню View>Surface редактора правил;

• командой меню View>Surface программы просмотра правил;

• нажатием клавиш <Ctrl>+<6>.

Графический интерфейс программы просмотра поверхности нечеткого вывода для разработанной нечеткой модели изображен на рисунке 3.9.

Эта программа служит для общего анализа адекватности нечеткой модели, позволяя оценить влияние изменения значений входных нечетких переменных на значение одной из выходных нечетких переменных. В случае необходимости можно получить график зависимости выходной переменной от одной из входных переменных. Для этого необходимо выбрать нужную переменную в раскрывающемся списке X (input),а в раскрывающемся списке Y (input) выбрать значение -попе-. Полученный график зависимости изображен на рисунке 3.10.

Полученный график зависимости соответствует среднему значению второй входной переменной ("качество ужина") в 5 баллов. Это значение может быть изменено пользователем, для чего следует ввести нужное значение в поле ввода Ref. Input:.Заметим, что значение NaN для первой входной переменной соответ­ствует ее изменению во всем интервале определения.

 

 

Рисунок 3.9.Вид программы просмотра поверхности нечеткого вывода для разработанной нечеткой модели

 

Заканчивая рассмотрение процесса разработки простейшей системы нечеткого вывода в интерактивном режиме, следует заметить, что наиболее эффективным этот способ оказывается для сложных нечетких моделей с большим числом переменных и правил нечеткого вывода. В этом случае задание переменных и функций принадлежности их термов в графическом режиме, а также визуализация правил позволяют существенно уменьшить трудоемкость разработки нечеткой модели, снизить количество возможных ошибок и сократить общее время нечеткого моделирования.

В то же время следует помнить, что количество переменных и правил в нечеткой модели, которые могут быть визуализированы, ограничено. В частности, если число входных переменных превышает 10, то их отображение в соответствующих графических редакторах происходит с искажениями.

Процесс разработки системы нечеткого вывода в режиме команд может дополнить, а в отдельных случаях, и заменить процесс разработки в интерактивном режиме, предоставляя пользователю полный контроль над всеми переменными рабочей области системы MATLAB.

 

 

Рисунок 3.10.График зависимости выходной переменной от первой из входных переменных для разработанной нечеткой модели