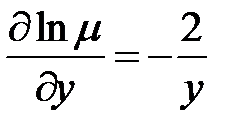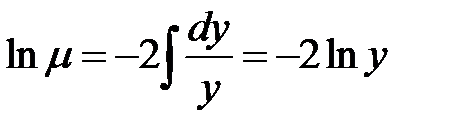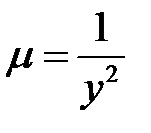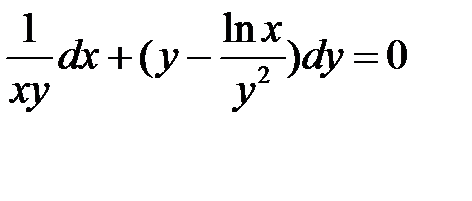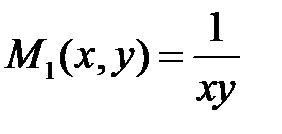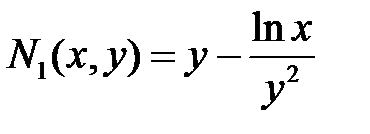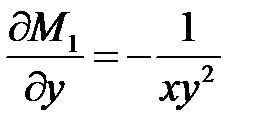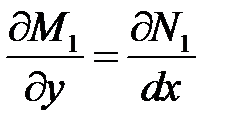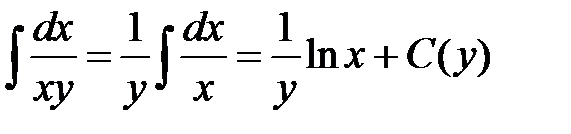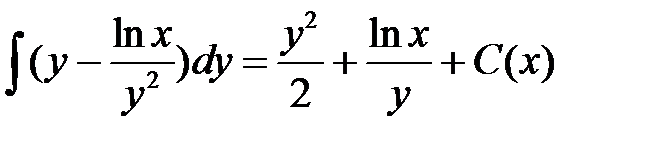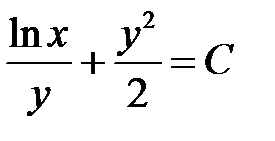Пусть для уравнения 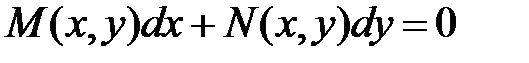 (1)
(1)
не выполняется условие  , т.е.
, т.е.  .
.
Иногда удается подобрать такую функцию 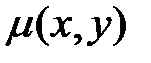 , после умножения на которую всех членов уравнения (1), левая часть уравнения становится полным дифференциалом. Общее решение полученного уравнения совпадает с общим решением первоначального уравнения. Функция
, после умножения на которую всех членов уравнения (1), левая часть уравнения становится полным дифференциалом. Общее решение полученного уравнения совпадает с общим решением первоначального уравнения. Функция 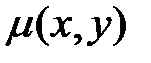 называется интегрирующим множителем уравнения (1).
называется интегрирующим множителем уравнения (1).
Найдем формулы, по которым можно вычислить интегрирующий множитель. Умножим обе части уравнения (1) на множитель  :
:
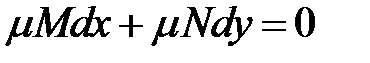
Для того, чтобы это уравнение было уравнением в полных дифференциалах, необходимо и достаточно выполнение условия
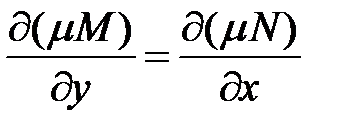
т.е. 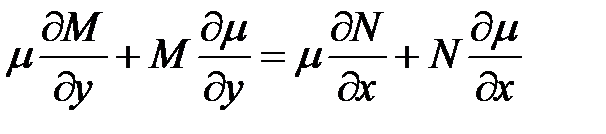
или 
Разделим обе части этого равенства на  , получим
, получим
 (2)
(2)
Всякая функция 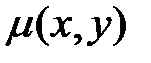 , удовлетворяющая уравнению (2), является интегрирующим множителем уравнения (1).
, удовлетворяющая уравнению (2), является интегрирующим множителем уравнения (1).
Уравнение (2) является уравнением в частных производных с неизвестной функцией  , зависящей от двух переменных х и у.
, зависящей от двух переменных х и у.
Задача нахождения 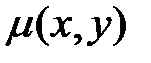 из уравнения (2) не из легких. Только в некоторых частных случаях удается найти функцию
из уравнения (2) не из легких. Только в некоторых частных случаях удается найти функцию 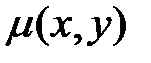 .
.
Пусть  - интегрирующий множитель, который зависит только от у, тогда
- интегрирующий множитель, который зависит только от у, тогда  .
.
Из уравнения (2) получаем обыкновенное дифференциальное уравнение  , из которого определим
, из которого определим  , а затем
, а затем  .
.
Его можно решить, если только выражение  зависит только от у.
зависит только от у.
Аналогично, если  - интегрирующий множитель, зависит только от х.
- интегрирующий множитель, зависит только от х.
Из уравнения (2) получим уравнение
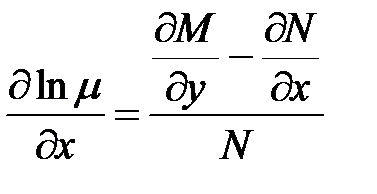
Решаем его, если выражение  зависит только от х.
зависит только от х.
Пример. Г.Н. Берман № 4061
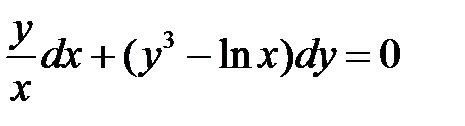
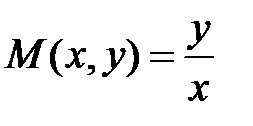
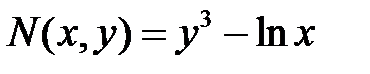
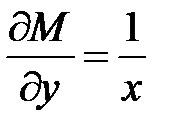
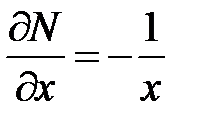
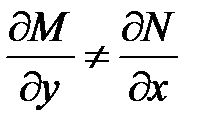
Выражение  не подходит
не подходит
Выражение  подходит
подходит
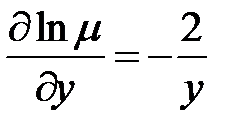
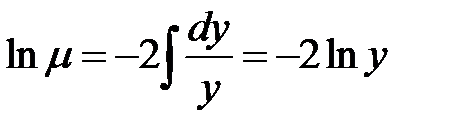
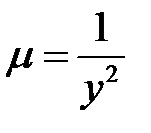
Умножим обе части данного уравнения на 
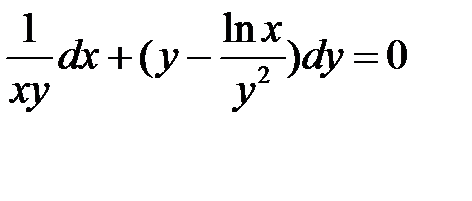
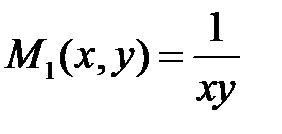
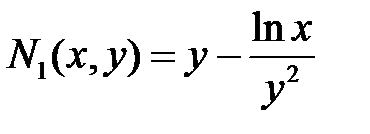
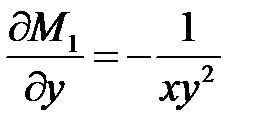

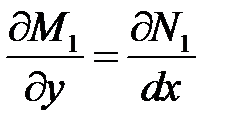
Новое уравнение есть уравнение в полных дифференциалах.
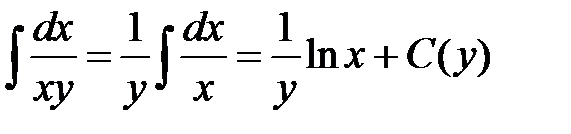
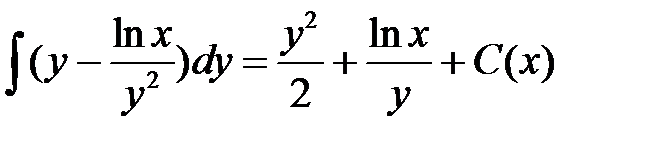
Общее решение данного уравнения
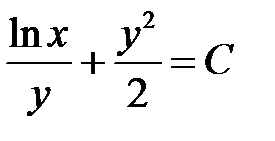
Коммерческое предложение
| Мы используем только высококачественные комплектующие (немецкий пластиковый профиль KBE и фурнитуру ROTO, профиль европейского качества MONTBLANC с фурнитурой VORNE), современное оборудование на производстве. 100% контроль качества при изготовлении пластиковых окон позволяют нам успешно работать! Скидка на КВЕ 20%, на Мonblanс 37%.
| |

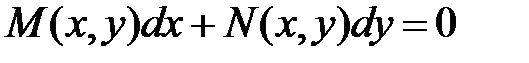 (1)
(1) , т.е.
, т.е.  .
.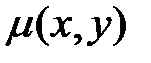 , после умножения на которую всех членов уравнения (1), левая часть уравнения становится полным дифференциалом. Общее решение полученного уравнения совпадает с общим решением первоначального уравнения. Функция
, после умножения на которую всех членов уравнения (1), левая часть уравнения становится полным дифференциалом. Общее решение полученного уравнения совпадает с общим решением первоначального уравнения. Функция  :
: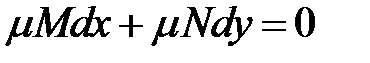
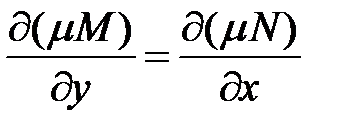
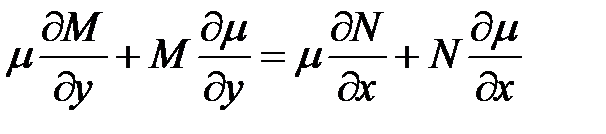

 (2)
(2) - интегрирующий множитель, который зависит только от у, тогда
- интегрирующий множитель, который зависит только от у, тогда  .
. , из которого определим
, из которого определим  , а затем
, а затем  зависит только от у.
зависит только от у. - интегрирующий множитель, зависит только от х.
- интегрирующий множитель, зависит только от х.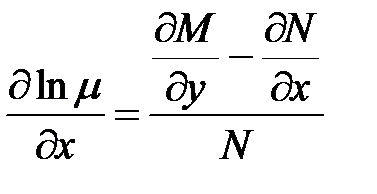
 зависит только от х.
зависит только от х.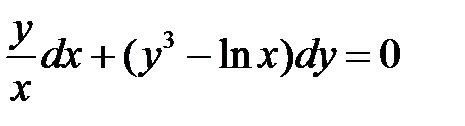
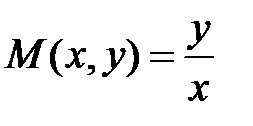
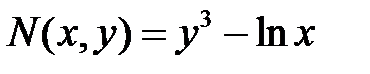
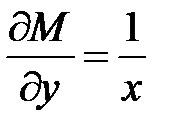
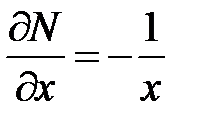
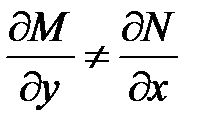
 не подходит
не подходит подходит
подходит