РЕШЕНИЕ ЗАДАЧ
КЛЮЧЕВЫЕ ЗАДАЧИ 1. Точка С – середина отрезка AB, а О – произвольная точка на плоскости (рис. 6). Доказать, что
По правилу треугольника
Так как точка С – середина отрезка АВ, то 2. Доказать, что средняя линия трапеции параллельна основаниям и длина ее равна полусумме длин оснований.
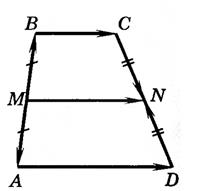
ABCD– трапеция M– середина AВ N– середина СD

Анализ. Для доказательства параллельности достаточно показать, что векторы Решение. 1) Согласно рассмотренной задаче 1 2) Так как 3) Так как MN = 3. Разделить данный отрезок AB в данном отношении m: n, то есть найти точку M принадлежит AB, такую, что AM: MB = m: n.
Решение: Очевидно, что M принадлежит AB делит отрезок AB в заданном отношении m: n тогда и только тогда, когда
Отсюда
Подставляя в исходное соотношение, имеем
откуда находим
В частности, если M – середина отрезка AB, то m = n, и получим
Если точки A и B заданы своими координатами в некоторой декартовой системе координат
где В частности, когда точка M является серединой отрезка AB, получаем
Таким образом, мы векторным путем получили результаты.
ЭЛЕМЕНТАРНЫЕ ЗАДАЧИ 4. Дан произвольный треугольник
|

 .
. Доказательство:
Доказательство: ,
, 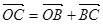 . Складывая эти равенства, получаем:
. Складывая эти равенства, получаем: .
. . Таким образом,
. Таким образом, 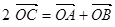 , или
, или  .
. Дано:
Дано: и
и  коллинеарны
коллинеарны .
.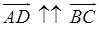 , то
, то  и, значит, MN || AD.
и, значит, MN || AD. = AD + BC, поэтому
= AD + BC, поэтому (AD + BC).
(AD + BC).
 Кроме того,
Кроме того,





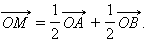
 то, используя формулу, можно легко найти координаты точки M в той же системе координат. Векторное равенство равносильно числовым равенствам
то, используя формулу, можно легко найти координаты точки M в той же системе координат. Векторное равенство равносильно числовым равенствам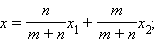

 и
и  – координаты концов отрезка AB, а x и y – координаты искомой точки M.
– координаты концов отрезка AB, а x и y – координаты искомой точки M.

 . Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника
. Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника 


