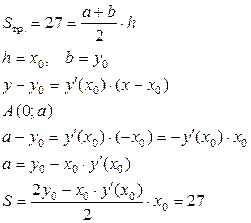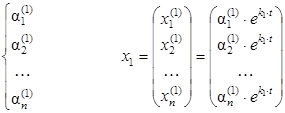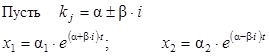Однородные системы с постоянными коэффициентами. Иногда, чтобы получить линейное уравнение, требуется поменять ролями x и y по теореме о производной обратной функции.
Пример:
Пример: Найти кривые, у которых площадь трапеций, ограниченных осями координат, касательной и ординатой точки касания, равна 27.
Системы дифференциальных уравнений.
Данная система записана в нормальном виде. Метод исключения. 1. Получим систему в виде:
2. Из первых (n – 1) уравнений полученной системы выразить x 2, x 3, …, xn и подставить в последнее уравнение. 3. Решить полученное уравнение (после его решения мы найдем x 1)
4. Найти x 2, x 3, …, xn, пользуясь соотношениями из второго пункта. Пример:
Пример:
Однородные системы с постоянными коэффициентами.
Система является определенной, т.е. имеет единственное решение, если D ¹ 0. Система всегда имеет тривиальное (нулевое) решение, поэтому, чтобы получить ненулевое решение потребуем D = 0. D = det (A – k × E) = 0 – характеристическое уравнение исходной системы. 1 случай: k 1, k 2, …, kn – различные и вещественные корни характеристического уравнения. С помощью k 1 из системы (1) получаем решение:
Аналогично получаем x 2, x 3, …, xn. Общее решение системы:
Пример:
2 случай: k 1, k 2, …, kn – различные, но среди них есть комплексные (могут быть все комплексные).
Очевидно, что x 1 и x 2 – комплексно-сопряженные (их вещественные и мнимые части равны), поэтому можно рассматривать один корень и, складывая отдельно вещественные, отдельно мнимые части, получить искомые решения. Пример:
|