Методы его нахождения
} ((Q ВЫБОР 1 ФАЙЛ)) Первообразной для функции f (x) на интервале (a, b) называется функция F (x), если... ((V ФАЙЛ)) f¢ (x) = F (x) ((V ФАЙЛ)) f¢; (x) = F¢; (x) ((V ФАЙЛ +)) F¢; (x) = f (x) ((V ФАЙЛ)) f (x) = F (x) ((Q ВЫБОР 1)) Первообразная функция F (x) для функции f (x) = cos x равна... ((V ФАЙЛ)) - cos x + C ((V ФАЙЛ)) - sin x + C ((V ФАЙЛ +)) sin x + C ((V ФАЙЛ)) cos x + C ((Q ВЫБОР 1 ФАЙЛ)) Первообразная для функции ((V ФАЙЛ)) arctg x + C ((V ФАЙЛ)) arcctg x + C ((V ФАЙЛ)) ctg x + C ((V ФАЙЛ +)) tg x + C ((Q ВЫБОР 1)) F (x) - одна из первообразных для функции f (x). Тогда любая первообразная F(x) для функции f (x) равна: ((V ФАЙЛ)) F(x) = F (x) + f (x) ((V ФАЙЛ)) F(x) = f (x) ((V ФАЙЛ +)) F(x) = F (x) + C ((V ФАЙЛ)) F(x) = F (x) ((Q ВЫБОР 1)) Первообразная функция F (x) для функции f (x) = x равна: ((V ФАЙЛ)) x + C ((V ФАЙЛ)) - x + C ((V ФАЙЛ +))
((V ФАЙЛ))
((Q СООТВ 1)) Соответствие первообразной F (x) функции f (x): ((V 1 1))
((V 1 2))
((V 1 3))
((V 1 4))
((V 1 5))
((V 1 6))
((V 2 1 ФАЙЛ))
((V 2 2 ФАЙЛ))
((V 2 3 ФАЙЛ))
((V 2 4 ФАЙЛ))
((V 2 5 ФАЙЛ))
((V 2 6 ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ)) F (x) - первообразная для функции f (x). Тогда неопределённым интегралом ((V ФАЙЛ)) сама первообразная F (x) ((V ФАЙЛ)) сумма F (x) + f (x) ((V+)) совокупность всех первообразных F (x) + C ((V)) совокупность всех функций f (x) + C, где С - произвольная постоянная ((Q ВЫБОР 1 ФАЙЛ))
((V)) f (x) ((V)) F (x) ((V+)) f (x) dx ((V)) F (x) dx где F (x) - первообразная функции f (x) ((Q ВЫБОР 1 ФАЙЛ)) F (x) - первообразная для функции f (x). Тогда ((V)) f (x) ((V)) F (x) ((V+)) f (x) + C ((V)) F (x) + C где С - произвольная постоянная ((Q ВЫБОР 1 ФАЙЛ))
((V)) ((V +)) С ((V)) ((V)) х ((Q ВЫБОР 1 ФАЙЛ))
((V)) ((V +)) х + С ((V)) х 2 ((V)) х 2 + С ((Q СООТВ 1)) Соответствие неопределённых интегралов функциям: ((V 1 1 ФАЙЛ))
((V 1 2 ФАЙЛ))
((V 1 3 ФАЙЛ))
((V 1 4 ФАЙЛ))
((V 1 5 ФАЙЛ))
((V 1 6 ФАЙЛ))
((V 2 1 ФАЙЛ))
((V 2 2 ФАЙЛ))
((V 2 3 ФАЙЛ))
((V 2 4 ФАЙЛ))
((V 2 5 ФАЙЛ))
((V 2 6 ФАЙЛ))
((Q СООТВ 1)) Соответствие функций неопределённым интегралам: ((V 1 1 ФАЙЛ))
((V 1 2 ФАЙЛ))
((V 1 3 ФАЙЛ))
((V 1 4 ФАЙЛ))
((V 1 5 ФАЙЛ))
((V 1 6 ФАЙЛ))
((V 2 1 ФАЙЛ)) ((V 2 2 ФАЙЛ))
((V 2 3 ФАЙЛ))
((V 2 4 ФАЙЛ))
((V 2 5 ФАЙЛ))
((V 2 6 ФАЙЛ))
((Q СООТВ 1)) Соответствие функций неопределённым интегралам: ((V 1 1 ФАЙЛ))
((V 1 2 ФАЙЛ))
((V 1 3 ФАЙЛ))
((V 1 4 ФАЙЛ))
((V 1 5 ФАЙЛ))
((V 1 6 ФАЙЛ))
((V 2 1 ФАЙЛ))
((V 2 2 ФАЙЛ))
((V 2 3 ФАЙЛ))
((V 2 4 ФАЙЛ))
((V 2 5 ФАЙЛ))
((V 2 6 ФАЙЛ))
((Q ВЫБОР 1))
((V)) x + C ((V ФАЙЛ)) 2 x 2 + C ((V ФАЙЛ +))
((V ФАЙЛ)) 2 x + C ((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V)) x = t ((V ФАЙЛ))
((V ФАЙЛ +)) t = x 2 ((V ФАЙЛ))
((Q ВЫБОР 1))
((V ФАЙЛ)) e 2 x + C ((V ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ)) 2 e 2 x + C ((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ +)) t = ln x ((V ФАЙЛ))
((V ФАЙЛ)) t = ln3 x ((V ФАЙЛ)) t = x ((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ)) (x 2 + 4) + C ((V ФАЙЛ)) ln(x 2 + 4) + C ((V ФАЙЛ +))
((Q СООТВ 1)) Соответствие функций неопределённым интегралам: ((V 1 1 ФАЙЛ))
((V 1 2 ФАЙЛ))
((V 1 3 ФАЙЛ))
((V 1 4 ФАЙЛ))
((V 1 5 ФАЙЛ))
((V 1 6 ФАЙЛ))
((V 2 1 ФАЙЛ))
((V 2 2 ФАЙЛ))
((V 2 3 ФАЙЛ))
((V 2 4 ФАЙЛ))
((V 2 5 ФАЙЛ))
((V 2 6 ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ)) Формула интегрирования по частям. ò udv равен... ((V ФАЙЛ +)) uv - ò vdu ((V ФАЙЛ)) u - ò vdu ((V ФАЙЛ)) vu - ò vdu ((V ФАЙЛ)) v - ò udv ((Q ВЫБОР 1 ФАЙЛ)) Применить формулу интегрирования по частям в интеграле ò x 2ln xdx при u =... ((V ФАЙЛ)) x 2 ((V ФАЙЛ)) x ((V ФАЙЛ)) x ln x ((V ФАЙЛ +)) ln x ((Q ВЫБОР 1 ФАЙЛ)) Применить формулу интегрирования по частям в интеграле ò x 2cos 2 xdx при u =... ((V ФАЙЛ)) cos2 x ((V ФАЙЛ +)) x 2 ((V ФАЙЛ)) x cos2 x ((V ФАЙЛ)) x ((Q ВЫБОР 1 ФАЙЛ)) ò xe - xdx равен... ((V ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ)) òarctg xdx равен... ((V ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ)) (x ± a) + C ((V ФАЙЛ))
((V ФАЙЛ +)) ln| x ± a | + C ((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ)) (x + 2)3 + C ((V ФАЙЛ +))
((V ФАЙЛ)) 2(x + 2)2 + C ((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ +)) arctg(x + 1) + C ((V ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ)) ln(x 2 + 4) + C ((V ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ)) arctg(x + 2) + C ((V ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ)) ln| x 2 - 4 x + 8 | + C ((V ФАЙЛ +))
((V ФАЙЛ))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ)) ln| x 2 - 4 x + 5 | + C ((V ФАЙЛ)) ln| x 2 - 4 x + 5 | ((V ФАЙЛ +)) ln| x 2 - 4 x + 5 | + 9arctg (x - 2) + C ((V ФАЙЛ)) arctg (x - 2) + C ((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ)) ln | x 2 + 4 | + C ((V ФАЙЛ +))
((V ФАЙЛ))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ)) Рациональная дробь (рациональная функции) ((V ФАЙЛ)) n £ m ((V ФАЙЛ)) n > m ((V ФАЙЛ +)) n < m ((V ФАЙЛ)) n = m ((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ)) ln | x - 2 | - ln | x + 5 | + C ((V ФАЙЛ +)) ln |(x - 2)(x + 5)| + C ((V ФАЙЛ)) ln | x + 5 | - ln | x - 2 | + C ((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ)) sin 2 x + C ((V ФАЙЛ +))
((V ФАЙЛ))
((V ФАЙЛ)) - sin 2 x + C ((Q ВЫБОР 1))
((V ФАЙЛ)) cos 3 x + C ((V ФАЙЛ))
((V ФАЙЛ)) - cos 3 x + C ((V ФАЙЛ +))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ)) ctg x + C ((V ФАЙЛ)) - ctg x + C ((V ФАЙЛ)) tg2 x + C ((V ФАЙЛ +))
((Q ВЫБОР 1))
((V ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((Q ВЫБОР 1))
((V ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ +))
((Q ВЫБОР 1))
((V ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ))
((V ФАЙЛ +))
((V ФАЙЛ))
((Q ВЫБОР 1 ФАЙЛ))
((V ФАЙЛ)) 2(x - ln (x + 1)) + C ((V ФАЙЛ +))
((V ФАЙЛ)) 2(x - ln (x + 1)) + C ((V ФАЙЛ))
((END)) методы его нахождения Функция F(x) называется первообразной для функции f(x) на интервале (a, b), если в каждой точке этого интервала выполняется равенство: F¢(x)=f(x) Пример 1. F(x)= sinx является первообразной для f(x)=cosx на интервале (-¥; +¥); т.к. (sinx) ¢=cosx Теорема (свойство первообразной). Если– две первообразные для f(x) на интервале (a, b), то они могут отличаться лишь на постоянную, т.е. F1(x) = F2(x) +С, где С – постоянная Следствие. Если функция F(x) – одна из первообразных для функции f(x), то любая её первообразная имеет вид: F(x)= F(x) +С, где С – постоянная. Совокупность всех первообразных для для функции f(x) на интервале (a, b) называется неопределённым интегралом от функции f(x) и обозначается:
Имеется таблица основных неопределённых интегралов(табличные интегралы):
|

 равна...
равна...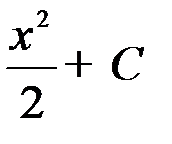










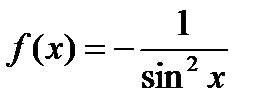


 называется...
называется... - дифференциал неопределённого интеграла равен...
- дифференциал неопределённого интеграла равен... равен...
равен...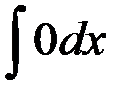 равен...
равен...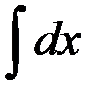 равен...
равен...
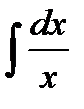





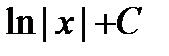















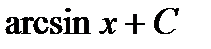


 :
:
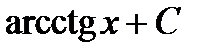

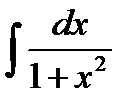




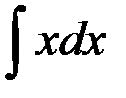 равен...
равен...
 равен...
равен...


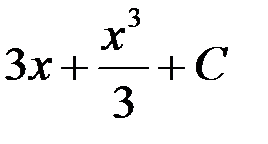
 равен...
равен...



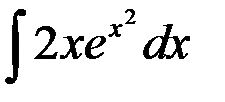 сводится к табличному заменой...
сводится к табличному заменой...
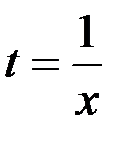
 равен...
равен...

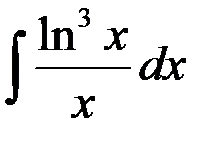 сводится к табличному заменой...
сводится к табличному заменой...
 равен...
равен...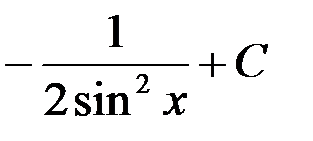



 равен...
равен...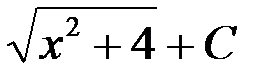




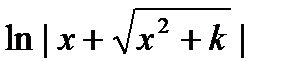



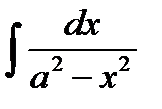
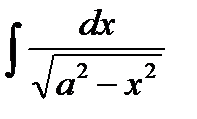

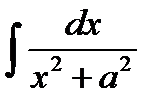




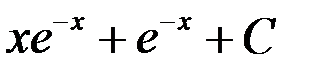




 равен...
равен...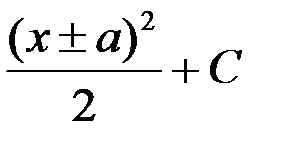

 равен...
равен...

 равен...
равен...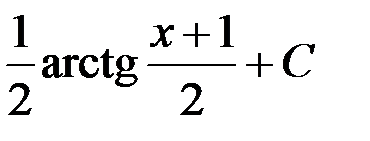


 равен...
равен...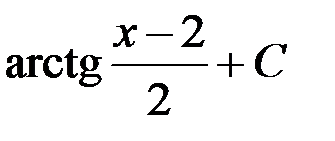



 равен...
равен...
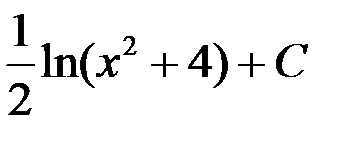

 равен...
равен...
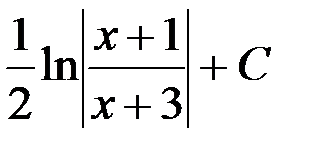

 равен...
равен...


 равен...
равен...
 равен...
равен...
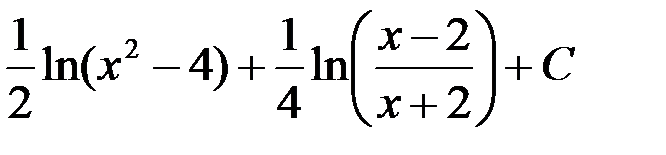

 (Pn (x), Qm (x) - многочлены степени n и m) является правильной, если...
(Pn (x), Qm (x) - многочлены степени n и m) является правильной, если... равен...
равен...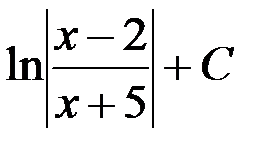
 равен...
равен...



 равен...
равен...

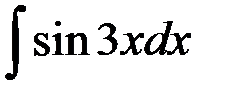 равен...
равен...

 равен...
равен...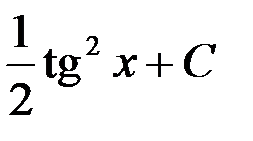
 равен...
равен...



 равен...
равен...



 равен...
равен...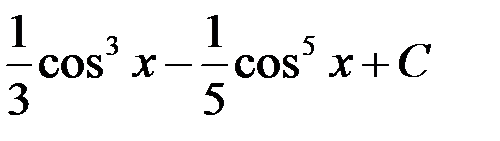



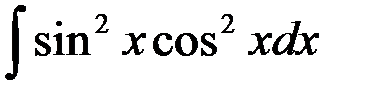 равен...
равен...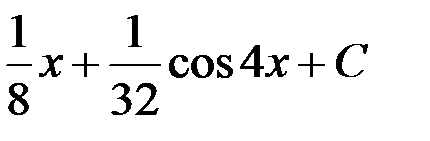

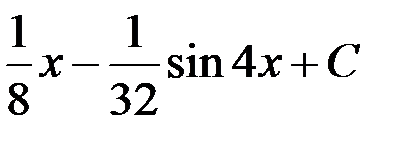

 равен...
равен...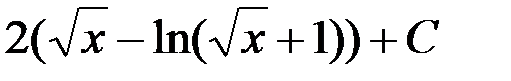





 Неопределённый интеграл обладает следующими основными свойствами:
Неопределённый интеграл обладает следующими основными свойствами:


